Part : Whole : : Arc : ?
Triangle
Square
Circle
Emigrant
The correct Answer is:C
Whole is the complete form of Part. Similarly, Circle is the complete form of Arc.
Topper's Solved these Questions
- ANALOGY OR SIMILARITY BOOK - KIRAN PUBLICATIONCHAPTER - ANALOGY OR SIMILARITY EXERCISE - TYPE-II
40 Videos
- ANALOGY OR SIMILARITY BOOK - KIRAN PUBLICATIONCHAPTER - ANALOGY OR SIMILARITY EXERCISE - TYPE-III
373 Videos
- ANALOGY OR SIMILARITY BOOK - KIRAN PUBLICATIONCHAPTER - ANALOGY OR SIMILARITY EXERCISE - TYPE-V
37 Videos
- ARRANGEMENT OF WORDS IN LOGICAL ORDER BOOK - KIRAN PUBLICATIONCHAPTER - ARRANGEMENT OF WORDS IN LOGICAL ORDER EXERCISE - TYPE II
199 Videos
Similar Questions
Comparison of parts of a whole may be done by a
View SolutionThe diagram shown two arcs, A and B. Arc A is part of the circle with centre O and radius OP . Arc B is part of the circle with centre M and radius PM , where is the mid-point of PQ. Show that the area enclosed by the two arcs is equal to 25(√3−π6)cm2
View Solution
Knowledge Check
A geometric representation, showing the relationship between a whole and its part, is
APie chartBBar graphCPictographDHistogramA certain number is divided into two parts such that 5 times the firsts part added to 11 times the second part makes 7 times the whole. The ratio of the first part to the second part is
A1:2B5:11C1:2D2:3Assertion: Animals such as sponge, Planaria, Hydra, can generate the whole body from a part.
Reason: Regeneration is quite common in animals.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf both assertion and reason are false.
A geometric representation showing the relationship between a whole and its parts is a
View SolutionState True or False ; If a whole or an object is divided into a number of equal parts, then each part represents a fraction.
View SolutionIn the figure , ΔQRS is an equilateral triangle.
Prove that
(1) arc RS ≅arcQS≅ arc QR
(2) m (arc QRS ) =240∘.
Proof :
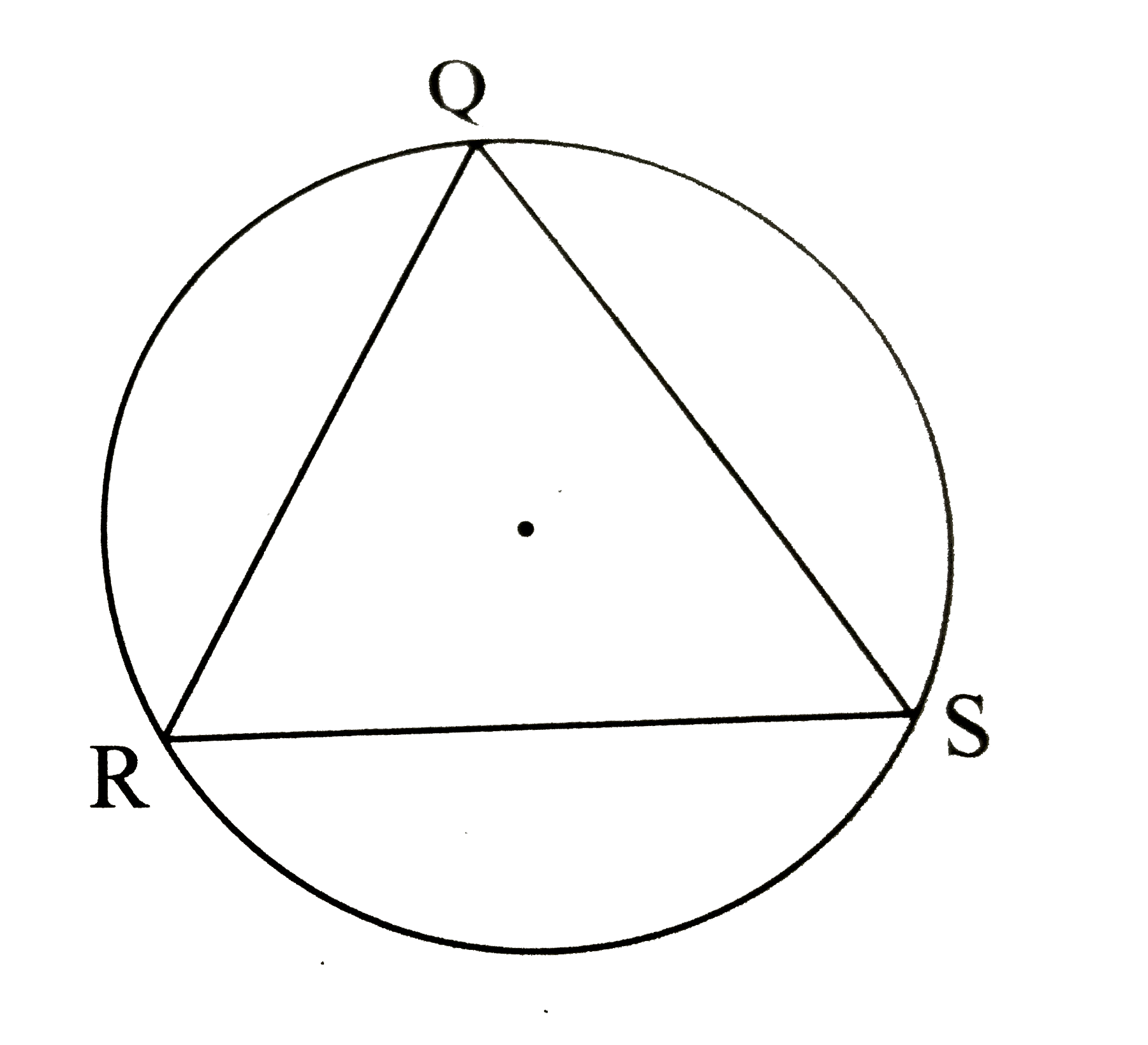
View SolutionIn figure, △QRS is an equilateral triangles. Prove that,
(1) arcRS≅arcQS≅arcQR
(2) m(arcQRS)=240∘.

View SolutionFind the value of : arcsin(12)+arccos(12)
View Solution
