A plate on square base made of brass is of length x cm and width 1mm. The plate weighs 4725 gm. If 1 cubic cm of brass weighs 8.4 gram, then the value of x is :
75
76
72
74
The correct Answer is:A
To solve the problem step by step, we will follow these calculations:
Step 1: Convert the width from mm to cm
The width of the plate is given as 1 mm. We need to convert it to centimeters since the length is in centimeters.
- Conversion: 1 mm=0.1 cm
Step 2: Calculate the volume of the plate
The volume V of the plate can be calculated using the formula for the volume of a rectangular prism:
V=length×width×thickness
Here, the length is x cm, the width is 0.1 cm, and we will denote the thickness as t (which is also in cm). However, since the thickness is not provided, we will assume it to be negligible for the sake of this calculation.
Step 3: Relate weight to volume
We know that the weight of the plate is given as 4725 grams. The weight can also be calculated using the density of brass:
Weight=Volume×Density
Given that the density of brass is 8.4 g/cm3, we can express the volume in terms of weight:
V=WeightDensity=4725 g8.4 g/cm3
Step 4: Calculate the volume
Now, we perform the calculation:
V=47258.4≈562.5 cm3
Step 5: Set up the equation for volume
Now we can set up the equation for the volume of the plate:
V=x×0.1 cm
So, we have:
x×0.1=562.5
Step 6: Solve for x
To find x, we rearrange the equation:
x=562.50.1=5625 cm
Step 7: Final value of x
Thus, the value of x is:
x=5625 cm
The width of the plate is given as 1 mm. We need to convert it to centimeters since the length is in centimeters.
- Conversion: 1 mm=0.1 cm
The volume V of the plate can be calculated using the formula for the volume of a rectangular prism:
V=length×width×thickness
Here, the length is x cm, the width is 0.1 cm, and we will denote the thickness as t (which is also in cm). However, since the thickness is not provided, we will assume it to be negligible for the sake of this calculation.
We know that the weight of the plate is given as 4725 grams. The weight can also be calculated using the density of brass:
Weight=Volume×Density
Given that the density of brass is 8.4 g/cm3, we can express the volume in terms of weight:
V=WeightDensity=4725 g8.4 g/cm3
Now, we perform the calculation:
V=47258.4≈562.5 cm3
Now we can set up the equation for the volume of the plate:
V=x×0.1 cm
So, we have:
x×0.1=562.5
To find x, we rearrange the equation:
x=562.50.1=5625 cm
Thus, the value of x is:
x=5625 cm
Topper's Solved these Questions
- MENSURATIONBOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - TYPE - III
21 Videos
- MENSURATIONBOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - TYPE - IV
169 Videos
- MENSURATIONBOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - Test Yourself
28 Videos
- LCM AND HCF BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself
18 Videos
- MISCELLANEOUSBOOK - KIRAN PUBLICATIONCHAPTER - MISCELLANEOUSEXERCISE - TYPE-VI
15 Videos
Similar Questions
A plate on square base made of brass is of length x cm and width 1 mm. The plate weighs 4725g .If 1cm3 of brass weighs 8.4 gram, then the value of x :
View SolutionA rectangular marble stone 28 cm wide and 5 cm thick weighs 112 kg. If 1 cubic cm of marble weighs 25 gm, then the length of given stone is
View Solution
Knowledge Check
A lead pipe is 35 cm long its external diameter is 2.4 cm and its thickness is 2 mm . If 1 cubic cm of lead weight 5 gms . The weight of pipe is -----
A220 gmsB242 gmsC420 gmsD484 gmsA plate has a length (5±0.1) cm and breadth (2±0.01) cm . Then the area of the plate is
A(10±0.25)cm2B(10±0.01)cm2C(10±0.001)cm2D(10±1)cm2If length and breath of a plate are (40±0.2)cm and (30±0.1)cm, the absolute error in the meaurement of area is
A10cm2B8cm2C9cm2D7cm2
Find the length of 13.2 kg of copper wire of diameter 4mm, when 1 cubic cm of copper weights 8.4 gm.
View SolutionThe dimensions of an open box are 50 cm, 40 cm and 23 cm. Its thickness is 3 cm. If 1 cubic cm of metal used in the box weighs 0.5 gms, find the weight of the box.
View SolutionTwo wires of diameter 0.25 cm, one made of steel and the other made of brass are loaded as shown in figure. The unloaded length of steel wire is 1.5 m and that of brass wire is 1.0 m. Compute the elongations of the steel and the brass wires .Young's modulus of steel is 2.0×1011Pa and that of brass is 9.1×1011 Pa.
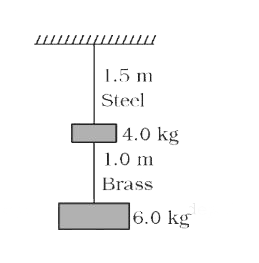
View SolutionHow many cubic centimetres of iron are there in an open box whose external dimensions are 36cm, 25cm and 16.5cm, the iron being 1.5cm thick throughout? If 1 cubic cm of iron weighs 15g, find the weight of the empty box in kg.
View SolutionA solid rectangular piece ofiron measures 1.05m×70cm×1.5cm. Find the weight of this piece in kilograms. If 1cm3 of iron weighs 8 grams.
View Solution
