Prove that the internal bisector of the angle A of a triangle ABC divides BC in the ratio AB:AC

If both assertion and reason are true and reason is the correct explanation of assertion .

If both assertion and reason are true but reason is not the correct explanation of assertion .

If assertion is true reason is false .

If assertion is false but reason is true .

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Answer

Step by step video, text & image solution for Prove that the internal bisector of the angle A of a triangle ABC divides BC in the ratio AB:AC by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.

Updated on:21/07/2023

Class 10 MATHS TRIANGLES

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
Assertion (A) : AD is angle bisector of $∠ A$ of the triangle ABC. If AB = 6 cm, BC = 7 cm, AC = 8 cm then BD = 3 cm and CD = 4 cm.
Reason (R) : The angle bisector AD of the triangle divides base BC in the ratio AB : AC.
ABoth Assertion A and Reason R are correct and Reason R is a correct explanation of Assertion A.
BBoth Assertion A and Reason R are correct but Reason R is not the correct explanation of Assertion A.
CAssertion A is correct, Reason R is wrong.
DAssertion A is wrong, Reason R is correct.
Question 2 - Select One
The internal /external bisector of an angled of a triangle divides the opposite side internally / externally in the ratio of the sides containing the angle .
In the given figure ,Ae is the bisector of the exterior $∠ C A D$ meeting BC produced in E . If AB=15 cm , AC = 8 cm and BC =14 cm , find CE .

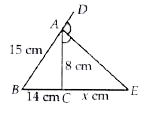A12 cm
B16 cm
C20 cm
D18 cm
Question 3 - Select One
In a triangle ABC, D is a point on BC such that AD is the internal bisector of $∠ A$ . Let $∠ B = 2 ∠ C$ and CD = AB. Then $∠ A$ is
A $18^{\circ}$
B $36^{\circ}$
C $54^{\circ}$
D $72^{\circ}$

MTG IIT JEE FOUNDATION-TRIANGLES - Exercise (Assertion & Reason Type)

Home
Ask Doubt
Profile

Prove that the internal bisector of the angle A of a triangle ABC divides BC in the ratio AB:AC

The correct Answer is:C

Topper's Solved these Questions

Similar Questions

Knowledge Check

Assertion (A) : AD is angle bisector of ∠A of the triangle ABC. If AB = 6 cm, BC = 7 cm, AC = 8 cm then BD = 3 cm and CD = 4 cm. Reason (R) : The angle bisector AD of the triangle divides base BC in the ratio AB : AC.

The internal /external bisector of an angled of a triangle divides the opposite side internally / externally in the ratio of the sides containing the angle . In the given figure ,Ae is the bisector of the exterior ∠CAD meeting BC produced in E . If AB=15 cm , AC = 8 cm and BC =14 cm , find CE .

In a triangle ABC, D is a point on BC such that AD is the internal bisector of ∠A. Let ∠B=2∠C and CD = AB. Then ∠A is

MTG IIT JEE FOUNDATION-TRIANGLES - Exercise (Assertion & Reason Type)

Assertion (A) : AD is angle bisector of $∠ A$ of the triangle ABC. If AB = 6 cm, BC = 7 cm, AC = 8 cm then BD = 3 cm and CD = 4 cm.
Reason (R) : The angle bisector AD of the triangle divides base BC in the ratio AB : AC.

In a triangle ABC, D is a point on BC such that AD is the internal bisector of $∠ A$ . Let $∠ B = 2 ∠ C$ and CD = AB. Then $∠ A$ is