In right angled ΔABC,∠C=90∘andD,E,F are three points on BC such that they divide it in equal parts .Then 8(AF2+AD2)=

AC2+AB2
11AC2+5AB2
10AC2+5AB2
None of these
The correct Answer is:B
Step by step video, text & image solution for In right angled DeltaABC,angleC=90^(@)andD,E,F are three points on BC such that they divide it in equal parts .Then 8(AF^(2)+AD^(2))= by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Exercise (Match the following )
3 Videos
- TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Exercise (Assertion & Reason Type)
5 Videos
- TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Exercise (Multiple Choice Questions) (LEVEL -1 )
35 Videos
- SURFACE AREAS AND VOLUMESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - OLYMPIAD/HOTS CORNER
20 Videos
Similar Questions
Consider a right-angled triangle ABC and ∠C=90∘. Suppose that the hypotenuse AB is divided into four equal parts by the points D, E, F such that AD= DE= EF= FB. If CD2+CE2+CF2=350, find the length of AB.
View SolutionABC is a right angled triangle , right angled at ∠B . If side AB is divided into three equal parts by points D and E such that D is nearest to A , then AC2−EC2DC2−BC2 is equal to :
View Solution
Knowledge Check
In right angled ΔABC,∠B=90∘, if P and Q are points on the sides AB and BC respectively, then :
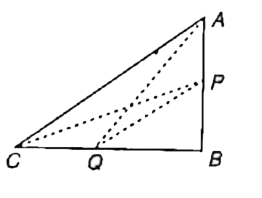 AAQ2+CP2=2(AC2+PQ2)BAQ2+CP2=AC2+PQ2C(AQ2+CP2)=12(AC2+PQ2)D(AQ+CP)=12(AC+PQ)
AAQ2+CP2=2(AC2+PQ2)BAQ2+CP2=AC2+PQ2C(AQ2+CP2)=12(AC2+PQ2)D(AQ+CP)=12(AC+PQ)In a right angled ΔABC,∠C=90∘andCD is the perpendicular on the hypotenuse AB,AB=c,BC=a,AC=bandCD=p, then :
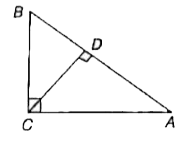 Apq=pbB1p2+1b2=1a2Cp2=b2+c2D1p2=1a2+1b2
Apq=pbB1p2+1b2=1a2Cp2=b2+c2D1p2=1a2+1b2In a right angled ΔABC,∠C=90∘andCD is the perpendicular on hypotenuse AB if BC = 15 cm and AC=20cm then CD is equal to :
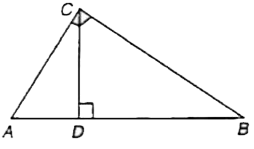 A18 cmB12 cmC17.5 cmDcan't be determined
A18 cmB12 cmC17.5 cmDcan't be determined
ΔABC is right angle triangle, where ∠B=90∘. D and E lies on sides AB and BC respectively, find the value of AC2+DE2?
View SolutionIn ΔABC,ifAC=8,BC=7 and D lies between A and B such that AD=2,BD=4, then the length CD equals
View SolutionL and M are the mid points of AB and BC respectively of ΔABC , right angled at B . 4LC2=
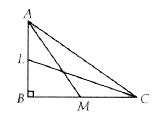
View SolutionGive a right angle triangle ABC with right angled at C. ∠C=90∘ and a,b,c are lengths of corresponding sides. (b>a). tan(A2) will be equal to
View SolutionD is a point on the side BC of a ΔABC such that AD bisects ∠BAC . Then
View Solution
