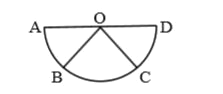
Assertion A : If A, B, C, D are four points on a semi-circular arc with centre at 'O' such that
∣∣∣−−→AB∣∣∣=∣∣∣−−→BC∣∣∣=∣∣∣−−→CD∣∣∣, then
−−→AB+−−→AC+−−→AD=4−−→AO+−−→OB+−−→OC
Reason R : Polygon law of vector addition yields
−−→AB+−−→BC+−−→CD+−−→AD=2−−→AO
Assertion A : If A, B, C, D are four points on a semi-circular arc with centre at 'O' such that |vec(AB)| = |vec(BC)|=|vec(CD)|, then vec(AB) +vec(AC) +vec(AD) =4 vec(AO) +vec(OB) +vec(OC) Reason R : Polygon law of vector addition yields vec(AB) +vec(BC) +vec(CD) +vec(AD)=2vec(AO) In the light of the above statements, choose the most appropriate answer from the options given below :
In the light of the above statements, choose the most appropriate answer from the options given below :

A

A is correct but R is not correct.

B

A is not correct but R is correct.

C

Both A and R are correct and R is the correct explanation of A.

D

Both A and R are correct but R is not the correct explanation of A.

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:D

Updated on:21/07/2023
|
Answer

Step by step video, text & image solution for Assertion A : If A, B, C, D are four points on a semi-circular arc with centre at 'O' such that |vec(AB)| = |vec(BC)|=|vec(CD)|, then vec(AB) +vec(AC) +vec(AD) =4 vec(AO) +vec(OB) +vec(OC) Reason R : Polygon law of vector addition yields vec(AB) +vec(BC) +vec(CD) +vec(AD)=2vec(AO) In the light of the above statements, choose the most appropriate answer from the options given below : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023
Class 12PHYSICSQUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • If ABCDE is a pentagon, then
    −−→AB+−−→AE+−−→BC+−−→DC+−−→ED+−−→AC is equal to

    A4−−→AC
    B2−−→AC
    C3−−→AC
    D5−−→AC

  • Let O be the centre of a regular pentagon ABCDE and −−→OA=→a, then −−→AB+−−−→2BC+−−−→3CD+−−−→4DE+−−−→5EA is equals:

    A0
    B4→a
    C5→a
    D6→a

  • Let O be the centre of a regular pentagon ABCDE and −−→OA=→a, then −−→AB+−−−→2BC+−−−→3CD+−−−→4DE+−−−→5EA is equals:

    A6→a
    B5→a
    C4→a
    D→0