PQRSTU is a cyclic hexagon. Then ∠P+∠R+∠Tis equal to
720∘
360∘
540∘
180∘
The correct Answer is:B
To solve the problem, we need to find the sum of angles ∠P+∠R+∠T in the cyclic hexagon PQRSTU.
1. Understand the Properties of a Cyclic Hexagon:
A cyclic hexagon is a hexagon where all vertices lie on a single circle. One important property of cyclic polygons is that the sum of the interior angles can be calculated using the formula:
Sum of interior angles=(n−2)×180∘
where n is the number of sides. For a hexagon, n=6.
2. Calculate the Sum of Interior Angles:
Using the formula:
Sum of interior angles=(6−2)×180∘=4×180∘=720∘
3. Divide the Angles:
In a cyclic hexagon, the sum of the angles can be divided into two groups:
∠P+∠R+∠T+∠Q+∠S+∠U=720∘
We can also note that the angles can be grouped as:
∠P+∠R+∠T=∠Q+∠S+∠U
4. Set Up the Equation:
Let:
∠P+∠R+∠T=x
Then:
∠Q+∠S+∠U=x
Therefore:
x+x=720∘
Simplifying gives:
2x=720∘
5. Solve for x:
Divide both sides by 2:
x=720∘2=360∘
Thus, the sum of angles ∠P+∠R+∠T is equal to 360∘.
Final Answer:
∠P+∠R+∠T=360∘
A cyclic hexagon is a hexagon where all vertices lie on a single circle. One important property of cyclic polygons is that the sum of the interior angles can be calculated using the formula:
Sum of interior angles=(n−2)×180∘
where n is the number of sides. For a hexagon, n=6.
Using the formula:
Sum of interior angles=(6−2)×180∘=4×180∘=720∘
In a cyclic hexagon, the sum of the angles can be divided into two groups:
∠P+∠R+∠T+∠Q+∠S+∠U=720∘
We can also note that the angles can be grouped as:
∠P+∠R+∠T=∠Q+∠S+∠U
Let:
∠P+∠R+∠T=x
Then:
∠Q+∠S+∠U=x
Therefore:
x+x=720∘
Simplifying gives:
2x=720∘
Divide both sides by 2:
x=720∘2=360∘
∠P+∠R+∠T=360∘
Topper's Solved these Questions
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - TRY YOURSELF
25 Videos
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIII)
70 Videos
- DISCOUNTBOOK - KIRAN PUBLICATIONCHAPTER - DISCOUNTEXERCISE - Test Yourself
10 Videos
- LCM AND HCF BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself
18 Videos
Similar Questions
In the given figure , PQRSTU is a regular hexagon of side 12 cm . What is the area (in cm2 ) of triangle SQU ?
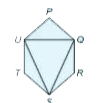
View SolutionIn the given figure PQRSTU is a regular hexagon of side 12 cm. what is the area (in cm2) of triangle SQU?
दी गई आकृति में, PQRSTU एक समषट्भुज है जिसकी भुजा 12 से.मी. हे। त्रिभुज SQU का क्षेत्रफल (से.मी.^2 में) क्या है?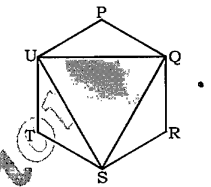
View Solution
Knowledge Check
nPr is equal to-
A⌊n⌊n⌊n−rB⌊n⌊n−rC⌊n⌋⌊n+rDNone of theseIf ABCDEF is regular hexagon, then AD+EB+FC is equal to
A0B2ABC3ABD4ABThe given infinite grid consists of hexagonal cell of six resistor each of resistance R. Then R12 is equal to
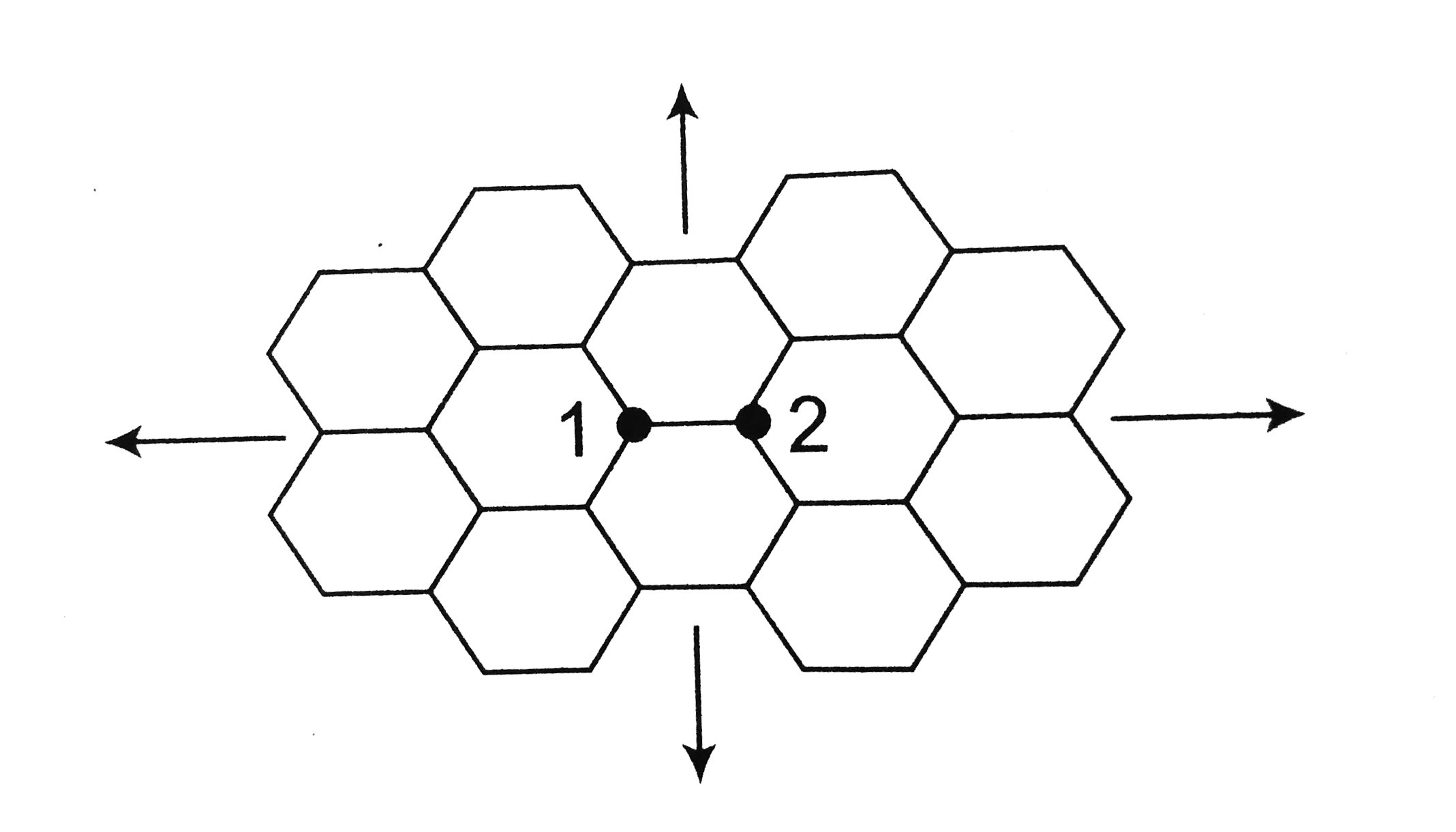 AR3B2R3C4R3D3R4
AR3B2R3C4R3D3R4
PQRSTU is a regular hexagon. Determine each angle of PQT .
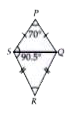
View SolutionPQRS is a kite.If ∠P=70∘ and ∠S=90.5∘,then ∠R equals
View SolutionIn Fig. 4.238, S and T are points on the sides PQ and PR respectively of PQR such that PT=2cm , TR=4cm and ST is parallel to QR . Find the ratio of the areas of PST and PQR . (FIGURE)
View Solutionsix charges of equal magnitude, 3 poistive and 3 negative are to be placed on PQRSTU corners of a regular hexagon, such that field at the centre is double that of what it would have been if only one +ve charge is placed at R. Which of the following arrangement of charge is posisble for P, Q, R, S, T and U respectively.
View Solutionsix charges of equal magnitude, 3 poistive and 3 negative are to be placed on PQRSTU corners of a regular hexagon, such that field at the centre is double that of what it would have been if only one +ve charge is placed at R. Which of the following arrangement of charge is posisble for P, Q, R, S, T and U respectively.

View Solution
