The distributions X and Y with total number of observations 36 and 64 and means 4 and 3 respectively are combined. What is the mean of the resulting distribution X+Y?
3.26
3.32
3.36
3.42
The correct Answer is:C
To find the mean of the combined distributions X and Y, we can follow these steps:
Step 1: Calculate the total value of distribution X
The total value of distribution X can be calculated using the formula:
Total value of X=Mean of X×Number of observations in X
Given:
- Mean of X = 4
- Number of observations in X = 36
Calculating:
Total value of X=4×36=144
Step 2: Calculate the total value of distribution Y
Similarly, we calculate the total value of distribution Y:
Total value of Y=Mean of Y×Number of observations in Y
Given:
- Mean of Y = 3
- Number of observations in Y = 64
Calculating:
Total value of Y=3×64=192
Step 3: Calculate the total value of the combined distribution X + Y
Now, we add the total values of distributions X and Y:
Total value of X + Y=Total value of X+Total value of Y
Calculating:
Total value of X + Y=144+192=336
Step 4: Calculate the total number of observations in the combined distribution
The total number of observations in the combined distribution is:
Total observations=Number of observations in X+Number of observations in Y
Calculating:
Total observations=36+64=100
Step 5: Calculate the mean of the combined distribution
Finally, we find the mean of the combined distribution using the formula:
Mean of X + Y=Total value of X + YTotal observations
Calculating:
Mean of X + Y=336100=3.36
Final Answer
The mean of the resulting distribution X + Y is 3.36.
---
The total value of distribution X can be calculated using the formula:
Total value of X=Mean of X×Number of observations in X
Given:
- Mean of X = 4
- Number of observations in X = 36
Total value of X=4×36=144
Similarly, we calculate the total value of distribution Y:
Total value of Y=Mean of Y×Number of observations in Y
Given:
- Mean of Y = 3
- Number of observations in Y = 64
Total value of Y=3×64=192
Now, we add the total values of distributions X and Y:
Total value of X + Y=Total value of X+Total value of Y
Calculating:
Total value of X + Y=144+192=336
The total number of observations in the combined distribution is:
Total observations=Number of observations in X+Number of observations in Y
Calculating:
Total observations=36+64=100
Finally, we find the mean of the combined distribution using the formula:
Mean of X + Y=Total value of X + YTotal observations
Calculating:
Mean of X + Y=336100=3.36
The mean of the resulting distribution X + Y is 3.36.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The distributions X and Y with total number of observations 36 and 64 and means 4 and 3 respectively are combined. What is the mean of the resulting distribution X+Y?
A3.26B3.32C3.36D3.42The distribution consists of three components with frequencies 45 , 40 and 15 having their means 2,2.5 and 2 respectively . The mean of the combined distribution is
A220B2.2C100D45A distribution consists of three components with frequencies 45, 40 and 15 having their means 2, 2.5 and 2, respectively. The mean of the combined. distribution is
A220B2.2C100D45
Consider the following frequency distribution
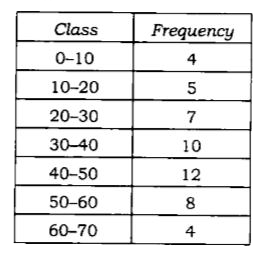
What is the mean of the distribution?
View SolutionWhat do you mean by frequency distribution polygon?
View SolutionWhat do you mean by frequency distribution?
View SolutionIf the total number of observations is 20,∑xi=1000and∑x2i=84000, then what is the variance of the distribution?
View SolutionRead the following frequency distribution for two series of observations and answer the two items that follow:
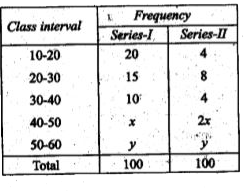
What is the mean of frequency distribution of Series-I ?
View Solution
