एक समानान्तर चतुर्भुज के दोनों कर्ण सदिश 3→i+→j−−→2k और →i−3→j+−→4k से व्यक्त किये जाते हैं। इस समानान्तर चतुर्भुज का क्षेत्रफल ज्ञात करें।
पहली विधि : माना कि ABCD एक समानान्तर चतुर्भुज है (चित्र-2.39) जिसका कर्ण A→C=3→i+→j−2→k और कर्ण D→B=→i−3→j+4→k .
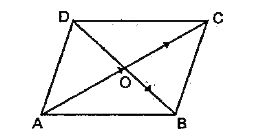
चूँकि समानान्तर चतुर्भुज के कर्ण एक-दूसरे को समद्विभाग करते है
∴A→O=12A→C=12(3→i+→j−2→k)
ओर O→B=12D→B=12(→i−3→j+4→k)
समानान्तर चतुर्भुज ABCD का सदिश क्षेत्रफल =4ΔAOB का सदिश
क्षेत्रफल 4×12A→O×O→B
=4×12[12(3→i+→j−2→k)×12(→i−3→j+4→k)]
=12∣∣
∣
∣∣→i→j→k31−21−34∣∣
∣
∣∣ =12→i(4−6)+→j(−2−12)+→k(−9−1) =12(−2→i−14→j−10→k)
=−(→i+→7j+5→k)
अतः अदिश क्षेत्रफल =√12+72+52=√75=5√3 वर्ग मात्रक
दूसरी विधि : माना कि A→B=→a ओर B→C=→b
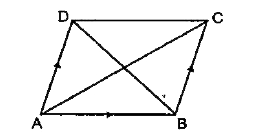
तब A→B+B→C=A→C
या →a+→b=3→i+→j−2→k
या −→b+→a=→i−3→j+4→k
समीकरण (i) और (it) को जोड़ने पर
−→2a=→4i−→2i+−→2k
∴→a=→2i−→j+→k
समीकरण (i) में से समीकरण (ii) को घटाने पर,
2→b=→2i+→4j−−→6k
∴→b=→i+2→j−3→k
ABCD समानातर चतुर्भुज का क्षेत्रफल
=A→B×B→C
=→a×→b
=(2→i×→j+→k)×(→i+2→j−3→k)
=∣∣
∣
∣∣→i→j→k2−1112−3∣∣
∣
∣∣
=→i(3−2)+→j(1+6)+→k(4+1)
=→i+7→j+5→k
अतः अदिश क्षे० = √12+72+52=√175=5√3 वर्ग मात्रक
Topper's Solved these Questions
- BOOK - STUDENTS FRIENDSCHAPTER - गतिकीEXERCISE - अभ्यासार्थ प्रश्नमाला ((A) वस्तुनिष्ठ प्रश्न :)23videos
गतिकी
- BOOK - STUDENTS FRIENDSCHAPTER - गतिकीEXERCISE - अभ्यासार्थ प्रश्नमाला ((B) रिक्त स्थानों को भरें)5videos
गतिकी
- BOOK - STUDENTS FRIENDSCHAPTER - गतिकीEXERCISE - अभ्यासार्थ प्रश्नमाला ((E) आंकिक:)5videos
गतिकी
- BOOK - STUDENTS FRIENDSCHAPTER - गति के नियम EXERCISE - अभ्यासार्थ प्रश्नमाला (आंकिक)12videos
गति के नियम
- BOOK - STUDENTS FRIENDSCHAPTER - गुरुत्वाकर्षण EXERCISE - अभ्यासार्थ प्रश्नमाला (आंकिक )14videos
गुरुत्वाकर्षण
Similar Questions
इनमें सदिश राशि कौन है?
01:35View SolutionF. r.............. राशि तथा F×r …………… राशि है।
01:46View Solutionअगर →a=→3i−4→j और →b=→8i+→6j तब →a,→b,→a+→b,→a−→b ओर →b−→a का मापांक और दिशा निकालें ।
01:17View Solutionकोई कण 0.15 मीटर त्रिज्या के वृत्तीय मार्ग पर प्रति सेकेण्ड 2 चक्कर लगाता है । कण के कोणीय वेग तथा अभिकेन्द्र त्वरण का मान ज्ञात कीजिए।
04:49View Solution20 किंग्रा और 30 किग्रा के दो गोले का केन्द्र एक दूसरे से 0.30 मी पर है। दोनों के बीच 124 मिलोग्राम भार का बल कार्य करता है । अगर पृथ्वी की त्रिज्या 6.4×106 मीटर हो, तो पृथ्वी की औसत घनत्व ज्ञात करें ।
02:09View Solution(vec i + xvec j + 3vec k) xx (vec i-vec j + vec k) = 5vec i + xvec j-3vec k then x =
04:04View SolutionThe moment of a force vec i+vec j+vec k acting through the point A=-2vec i+3vec j+vec k about the point B=vec i+2vec j+3vec k is
04:43View Solutionयदि →a=→i+→j+3→k,→n=2→i+3→j−5→k तब →a.→b=
02:42View SolutionFind the angle between the vectors →i+2→j+3→k and 3→i−→j+2→k.
02:11View Solution5→i+→j−3→k और 3→i−4→j+7→k का अदिश गुणनफल ज्ञात कीजिए।
02:54View Solution(→a.→b)→c और →b.→k का मान निकालें, जबकि
→a=3→i+2→j−→k,→b=→i−→j+3→k,→c=−2→i−3→j+→k.02:24View Solutionसदिश →a=2→i−3→j+→k तथा →b=3→i−→j−2→k के बीच के कोण की ज्या (sine) निकालें।
03:56View Solutionवह सदिश क्या होगा जो सदिश →i−→j+→k और 2→i+3→j−→k में से प्रत्येक पर लंब हो ?
02:42View Solutionयदि →a=→i+→j+→k,→b=2→i−→j+3→k और →c=→i−2→j+→k तो निम्नलिखित ज्ञात करे
2→a−→b+3→c के समांतर इकाई सदिश03:43View Solutionयदि →a=ˆi+ˆj+ˆk,→b=2ˆi−ˆj+3ˆk और →c=ˆi−2ˆj+ˆk तो सदिश 2→a−→b+3→c के समांतर एक मात्रक सदिश ज्ञात कीजिए ।
02:57View SolutionLet →a=4→i+3→j and →b=3→i+4→j. Find the magnitudes of (a)→a,(b)→b,(c)→a+→band (d)→a−→b
03:10View Solution
