1 kg द्रव्यमान का एक ब्लॉक क्षैतिज से के कोण पर झुके रुक्ष आनत तल पर रखा है और बल नियतांक वाले हल्के स्प्रिंग से चित्र 1.5 - 4 के अनुसार जुड़ा है। ब्लॉक को विरामावस्था से उस समय मुक्त किया जाता है जब स्प्रिंग अपनी शिथिल स्थिति (relaxed position) में है। यदि गुटका आनत तल पर पुनः विराम में आने से पहले 10 cm नीचे खिसक जाता हो , तो गुटके एवं आनत तल के बीच घर्षण गुणांक ज्ञात करे। यह मान ले कि स्प्रिंग का द्रव्यमान उपेक्षणीय है, तथा घिरनी घर्षणरहित है। 
ब्लॉक पर चाल बल चित्र 1. 5 - 5 में प्रदर्शित दिशाओ में कार्य करते है
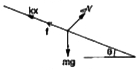
(i) गुरत्वीय बल = भार = mg ऊर्ध्वाधरतः नीचे की और
(ii ) आनत तल की अभिलंब प्रतिक्रिया N
(iii) स्प्रिंग - बल kx जहाँ x = स्प्रिंग का प्रसार तथा
(iv) घर्षण बल
कार्य - ऊर्जा प्रमेय के अनुसार सभी बलों द्वारा संपादित कार्य = गतिज ऊर्जा का परिवर्तन
अब mg के कारण कार्य
N के कारण कार्य चूँकि बल एवं विस्थापन परस्पर लंबवत है
स्प्रिंग बल के कारण कार्य घर्षण बला के कारण कार्य
कुल कार्य
कार्य - ऊर्जा प्रमेय से . . . (1)
क्योकि गतिज ऊर्जा का प्रारंभिक एवं अंतिम मान दोनों शून्य है
प्रश्न से तथा
समीकरण (1) में यह मान रखने पर
या
अतः अभीष्ट घर्षण गुणांक
Topper's Solved these Questions
- सामान्य भौतिकीBOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1.6 वृत्तीय गति
17 Videos
- सामान्य भौतिकीBOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1.7 आवेग एवं संवेग
20 Videos
- सामान्य भौतिकीBOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1.4 गति के नियम : घर्षण
33 Videos
- सरल रेखा एवं समतल, में कण की गति BOOK - DAS GUPTACHAPTER - सरल रेखा एवं समतल, में कण की गति EXERCISE - प्रश्नावली (आंकिक प्रश्न)
24 Videos
Similar Questions
1.5 m लंबी डोरी के एक सिरे पर किसी पत्थर को बाँधकर फर्श से 2m ऊँचाई पर क्षैतिज वृत्तीय पथ पर एकसमान चाल से घुमाया जाता है। गति के क्रम से डोरी के अचानक टूट जाने पर पत्थर प्रक्षेप्य गति करता हुआ 10 m की दुरी पर फर्श से टकराता है पत्थर की वृत्तीय गति में अभिकेंद्र त्वरण का मान ज्ञात करे।
View Solution1 kg तथा 16 kg द्रव्यमान के दो ब्लॉक की गतिज उर्जाएँ समान उनके रैखिक संवेग का अनुपात ज्ञात करे।
View Solution50 g द्रव्यमान का एक पत्थर ऊर्ध्वाधरतः ऊपर की ओर फेंका गया है। निम्नांकित परिस्थितियों के लिए पत्थर पर लग रहे नेट बल का परिमाण एवं दिशा बताए।
(a)ऊपर की ओर गति के क्रम में
(b) नीचे की ओर गति के क्रम में
(c) गति के उच्चतम बिंदु पर जहाँ पत्थर क्षणिक विराम (momentary rest) में रहता है
(d) विराम में स्थित रेलगाड़ी की खिड़की से पत्थर को गिराने के तुरंत बाद
View Solutionएक बस का समय-वेग ग्राफ चित्र में दिखाया गया है। निम्नलिखित का मान निकालें-(i) किस समयांतराल में बस की चाल एकसमान है, (ii) किस समयांतराल में बस की गति त्वरित है, (ii) बस कुल कितनी दूरी चलती है, (iv) वह समयांतराल जिसमें बस की गति अवमंदित है तथा अवमंदन का मान क्या है?
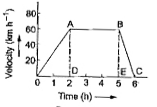
View Solutionएकसमान विद्युत क्षेत्र E=3×103ˆi(N)/C पर विचार कीजिये ।
(a) इस क्षेत्र का 10 cm भुजा के वर्ग के उस पार्श्व से जिसका तल yz तल के समांतर है, गुजरने वाला फ्लक्स क्या है ?
(b) इस वर्ग से गुजरने वाला फ्लक्स कितना है यदि इसके तल का अभिलंब x- अक्ष से 60∘ कोण बनता है ?
View Solutionद्रव्यमान m के एक कण को गति y=ut+12gt2 से वर्णित है । उस कण पर लगने वाले बल को ज्ञात करो ।
View Solutionयदि R त्रिज्या का एक वृत्त मूलबिंदु O से होकर जाता है तथा निर्देशांक अक्षो को A और B पर कट्टा है , तो O से रेखा AB पर डाले गए लम्ब के पाद का बिन्दुपथ है
View Solutionएक कोण पर झुके हुए तल पर ऊँचाई से प्रक्षेप्य
View Solution(-1-1) और (4, 2) से समान दूरी पर स्थित बिन्दुओं के बिन्दुपथ का समीकरण है
View Solution5 बार और 300K पर एक आदर्श एक्परमाणविक गैस के दो मोल के 1 बार के ब्रह्म डाब तक अनुत्क्रमणीय रूप से प्रसारित किया जाता है गैस दवरा किया गया कार्य xR (बार लीटर में ) है x का मान है
View Solutionसही कथनों का चयन कीजिए।
(1) जब क्लोरीन गैस को फेरस ब्रोमाइड के विलयन के माध्यम से बुदबुदाया जाता है तो फेरिक ब्रोमाइड प्राप्त होता है।
(2) जब SO2(g),H2O(g) और वायु को गर्म सोडियम क्लोरीन पर प्रवाहित किया जाता है तो सोडियम सल्फेट प्राप्त होता है।
(3) जब एलुमिनियम सल्फाइड आर्द्र हो जाता है। तब H2S गैस मुक्त होती है।
View Solutionजब NaCl और K_(2)Cr_(2)O_(7) के मिश्रण को धीरे-धीरे सांद्र H_(2)SO_(4) के साथ गर्म किया जाता है तो निम्नलिखित में से कौन सा कथन सही है? 1. एक गहरी लाल वाष्प मुक्त होती है। 2. जब वाष्प को NaOH विलयन में प्रवाहित किया जाता है, तो Na_(2)CrO_(4) का एक पीला विलयन प्राप्त होता है। 3. क्लोरीन गैस मुक्त होती है। 4. क्रोमिल क्लोराइड का निर्माण होता है।
View Solutionजब धातु M को NaOH के साथ उपचारित किया जाता है, तो एक श्वेत जिलेटिन जैसा अवक्षेप 'X' प्राप्त होता है, जो NaOH के आधिक्य में घुलनशील होता है। यौगिक 'X' प्रबल रूप से गर्म करने पर एक ऑक्साइड देता है जिसका उपयोग वर्णलेखिकी में एक अधिशोषक के रूप में किया जाता है। धातु 'M' है:
View Solutionदो द्रवों A और B के एक आदर्श मिश्रण को पिस्टन युक्त एक सिलेण्डर में रखा जाता है। पिस्टन को समतापीय रूप से खीचने पर द्रव का आयतन घटता है लेकिन वाष्प का आयतन बढ़ जाता है। द्रव की बहुत छोटी मात्रा शेष बचती है और वाष्प में A का मोल प्रभाज 0.4 होता है। यदि प्रायोगिक ताप पर P_(A)^(@) = 0.4 और P_(B)^(@) = 1.2 atm है, तो निम्नलिखित में से किस कुल दाब पर द्रव लगभग वाष्पीकृत हो जाता है?
View Solutionप्रायौगिक रूप से विरामावस्था पर एक इलेक्ट्रॉन को प्रारंभ में 100 वोल्ट के विभवान्तर से त्वरित किया जाता है। इसके बाद इसकी दे ब्राग्ली (de broglie) तंरग दैर्ध्य =lamda_(1)Å हो जाती है। फिर 19 वोल्ट के माध्यम से इसका मंदन किया जाता है जिससे इसकी तरंग दैर्ध्य lamda_(2) Å हो जाती ह। 3.2 वोल्ट के माध्यम से इसका और मंदन इसकी तरंग दैर्ध्य को lamda_(3) में बदल देता है। (lamda_(3)-lamda_(2))/(lamda_(1)) का मान क्या है?
View SolutionNaCl के संकुलन प्रभाज के लिए निम्नलिखित में से कौन सा व्यंजक सही है, यदि एक फलक और एक विकर्ण से a- आयन को हटा दिया जाता है?
View Solution
