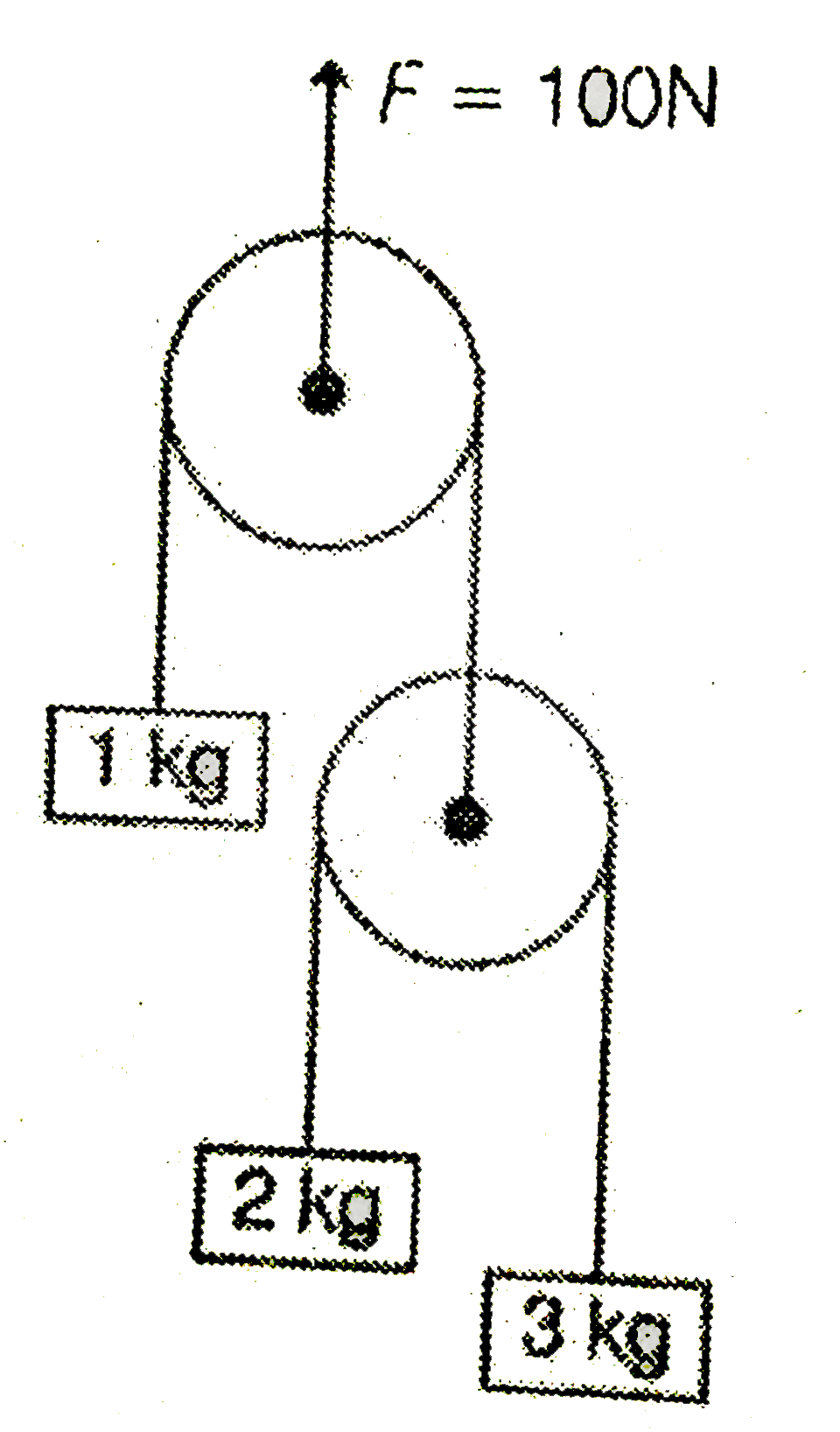
Find the accelerations of two blocks. Assume pulleys and strings are massless and frictionless. Also assume the string to be inextensible.
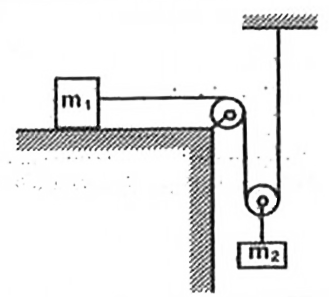
Y+2x+Z=l ...(i)
Y+X+l2+X+l2+Z−l1=l ...(ii)
Subtracting eq. 1st from eq. 2nd, we get 2l2=l1
Differentiating twice this equation w.r.t time we get ∴a1=2a2
i.e. acceleration of block m1 is twice the acceleration of block m2
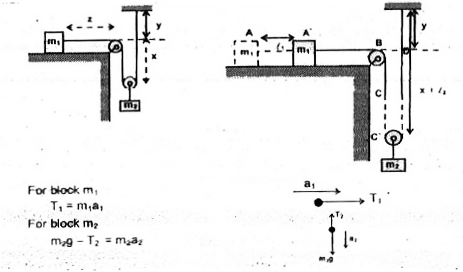
For block m1
T1=m1a1
For block m2
m2g−T2=m2a2
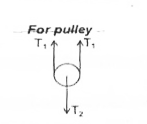
T1=T2 [∵Pulley is massless]
Let a2=a ∴t=2m1a
∴a1=2a, m2−2T=m2a
T1=T Solving a2=m2gm2+4m1
∴T2=2T ∴a1=2a2=2m2gm2+4m1
Similar Questions
Find the acceleration of blocks in fig. The pulley and the string are massless.

View SolutionFind the relation between acceleration of the two blocks m1andm2. Assume pulleys are massless and frictionless and the strings are inextensible .
View SolutionThe time period of block of mass m is (Assume pulleys and string are massless)
_PHY_E06_345_Q01.png) .
.
View Solution
Find out the acceleration of the blocks and tensions in the strings.
View SolutionFind the acceleration of the 6 kg block in the figure. All the surfaces and pulleys are smooth. Also the strings are inextensible and light. [Take g=10m/s2]
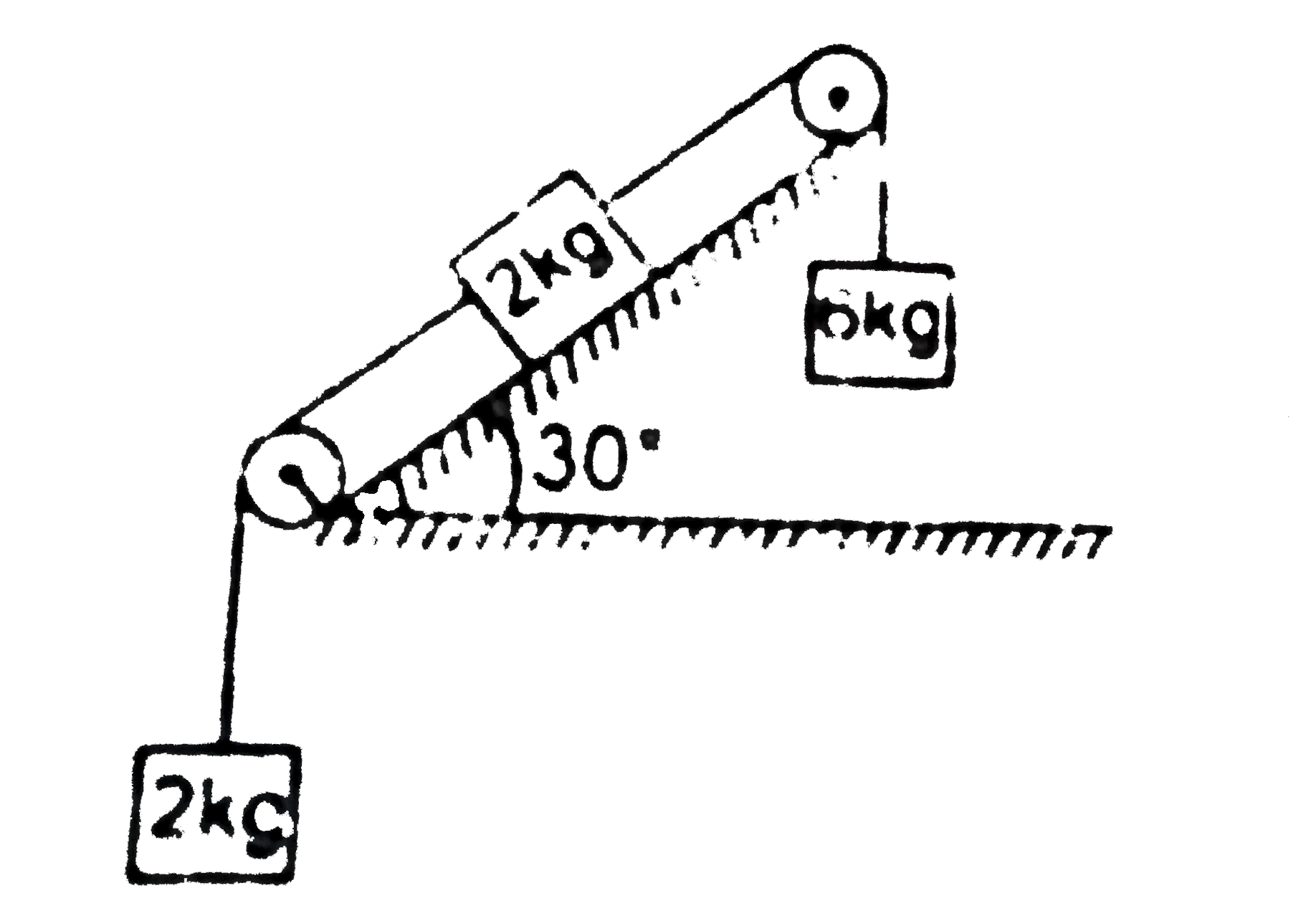 .
.
View Solution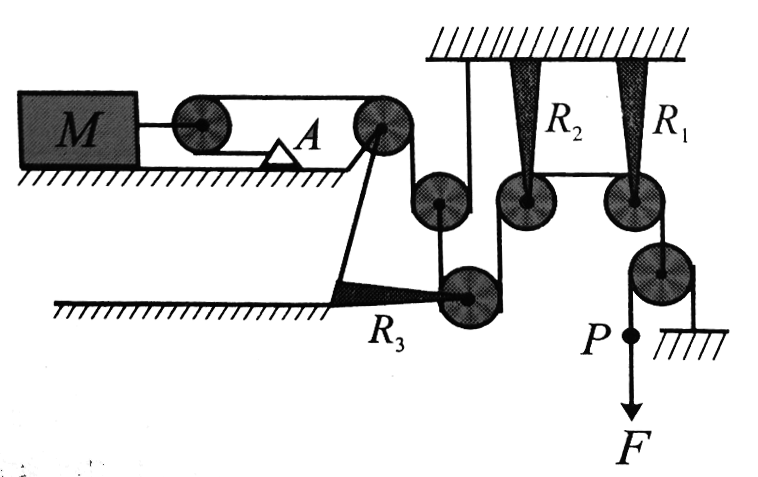
In the given arrangement, mass of the block is M and the surface on which the block is placed is smooth. Assuming all pulleys to be massless and frictionless, strings to be inelastic and light, R1,R2 and R3 to be light supporting rods, then acceleration of point P will be (A is fixed):
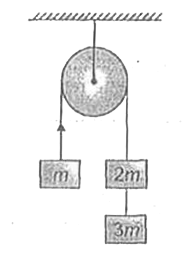
View SolutionFind the acceleration of two masses as shown in figure . The pulley are light and frictionless and string are light and frictionless and string are light and inextensible.

View SolutionIn the figure given below, with what acceleration does the block of mass m will move? (Pulley and strings are massless and frictionless)
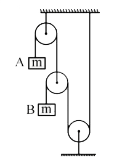
View SolutionIn the arrangement shown, the pulleys and strings are massless. The acceleration of block B is :
View SolutionIn the diagram shown in figure, both pulleys and strings are massless. The acceleration of 2 kg block is
View Solution
