Two blocks of masses and M are at rest on an inclined plane and are separated by a distance of as shown. The coefficient of friction between each block and the inclined plane is . The block is given a velocity of up the inclined plane. It collides with M, comes back and has a velocity of when it reaches its initial position. The other block M after the collision moves up and comes to rest. Calculate the coefficient of restitution between the blocks and the mass of the block M.
[Take and ]
![Two blocks of masses 2kg and M are at rest on an inclined plane and are separated by a distance of 6.0m as shown. The coefficient of friction between each block and the inclined plane is 0.25. The 2kg block is given a velocity of 10.0m//s up the inclined plane. It collides with M, comes back and has a velocity of 1.0m//s when it reaches its initial position. The other block M after the collision moves 0.5m up and comes to rest. Calculate the coefficient of restitution between the blocks and the mass of the block M. [Take sintheta=tantheta=0.05 and g=10m//s^2]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/DCP_V02_CH11_E01_193_Q01.png)
For the block of mass 2 kg (=m) in going from the A to B
of
Substituting the given data, we get
Or,
For the block of mass 2 kg (=m) coming back from the position B to A
Substituting the given data, we get
Or

For the block of Mass M in going from the position B to C
or
Similar Questions
A block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal. If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View Solution
Knowledge Check
A block of mass 3 kg rests on a rough inclined plane making an angle of 30∘. With the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A9.8 NB0.7×9.8×√3 NC9.8×√3 ND0.7×9.8 NA block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A10.3NB23.8NC11.9ND6.3NTwo blocks each of mass M are resting on a frictionless inclined plane as shown in fig then:
 AThe block A moves down the planeBThe block B moves down the plane.CBoth the blocks remain at restDBoth the blocks move down the plane.
AThe block A moves down the planeBThe block B moves down the plane.CBoth the blocks remain at restDBoth the blocks move down the plane.
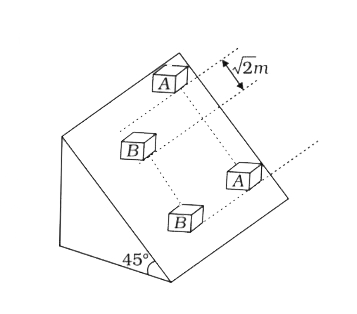
Two identical blocks A and B of equal masses are placed on rough inclined plane as shown in the figure. Initially the block A is √2m behind the block B. Coefficient of kinetic friction for the blocks A and B are 0.2 and 0.3 respectively (g=10m/s2). By the time the two blocks come on the same line on the inclined plane if they are released simultaneously, the distance moved by B is βm Find the value of β
View SolutionFind the force required to pull a block of mass 100kg up an incline of 8∘ at a uniform speed of 5m/s. The coefficient of friction between the block and the plane is 0.3.
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View SolutionA block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionA block of mass 2 kg slides down an incline plane of inclination 30°. The coefficient of friction between block and plane is 0.5. The contact force between block and plank is :
View Solution
