200V A.C. is applied at the ends of an LCR circuit. The circuit consists of an inductive reactance XL=50Ω capacitive reactance Xc=50Ω and ohmic resistance R = 10 Ω . Calculate the impedance of the circuit and also potential differences across L and R What will be the potential difference across L-C
To solve the problem step by step, we will calculate the impedance of the LCR circuit, the potential differences across the inductor (L) and resistor (R), and the potential difference across the LC combination.
Step 1: Calculate the Impedance (Z) of the Circuit
The impedance of an LCR circuit is given by the formula:
Z=√R2+(XL−XC)2
Where:
- R=10Ω
- XL=50Ω (inductive reactance)
- XC=50Ω (capacitive reactance)
Since XL=XC, we have:
XL−XC=0
Thus, the formula simplifies to:
Z=√R2=R=10Ω
Step 2: Calculate the Current (I) in the Circuit
Using Ohm's Law, the current can be calculated as:
I=VZ
Where:
- V=200V
- Z=10Ω
Substituting the values:
I=20010=20A
Step 3: Calculate the Potential Difference Across the Resistor (V_R)
The potential difference across the resistor is given by:
VR=I×R
Substituting the values:
VR=20×10=200V
Step 4: Calculate the Potential Difference Across the Inductor (V_L)
The potential difference across the inductor is given by:
VL=I×XL
Substituting the values:
VL=20×50=1000V
Step 5: Calculate the Potential Difference Across the LC Combination
Since XL=XC, the potential difference across the LC combination is:
VLC=VL−VC
Where VC is the potential difference across the capacitor, which can be calculated as:
VC=I×XC
Substituting the values:
VC=20×50=1000V
Thus:
VLC=VL−VC=1000−1000=0V
Summary of Results
- Impedance Z=10Ω
- Potential difference across the resistor VR=200V
- Potential difference across the inductor VL=1000V
- Potential difference across the LC combination VLC=0V
The impedance of an LCR circuit is given by the formula:
Z=√R2+(XL−XC)2
Where:
- R=10Ω
- XL=50Ω (inductive reactance)
- XC=50Ω (capacitive reactance)
XL−XC=0
Thus, the formula simplifies to:
Z=√R2=R=10Ω
Using Ohm's Law, the current can be calculated as:
I=VZ
Where:
- V=200V
- Z=10Ω
I=20010=20A
The potential difference across the resistor is given by:
VR=I×R
Substituting the values:
VR=20×10=200V
The potential difference across the inductor is given by:
VL=I×XL
Substituting the values:
VL=20×50=1000V
Since XL=XC, the potential difference across the LC combination is:
VLC=VL−VC
Where VC is the potential difference across the capacitor, which can be calculated as:
VC=I×XC
Substituting the values:
VC=20×50=1000V
Thus:
VLC=VL−VC=1000−1000=0V
- Impedance Z=10Ω
- Potential difference across the resistor VR=200V
- Potential difference across the inductor VL=1000V
- Potential difference across the LC combination VLC=0V
Similar Questions
In an experiment, 200V AC is applied at the end of an LCR circuit. The circuit consists of an inductive reactance
(XL) =50Ω, capacitive reactance
(Xc)=50Ω, and capacitives resistance
(R)=10Ω, The impendance of the circuit is
View SolutionIn L-R circuit, resistance is 8Ω and inductive reactance is 6Ω then impedance is:
View SolutionIn the given circuit, calculate -
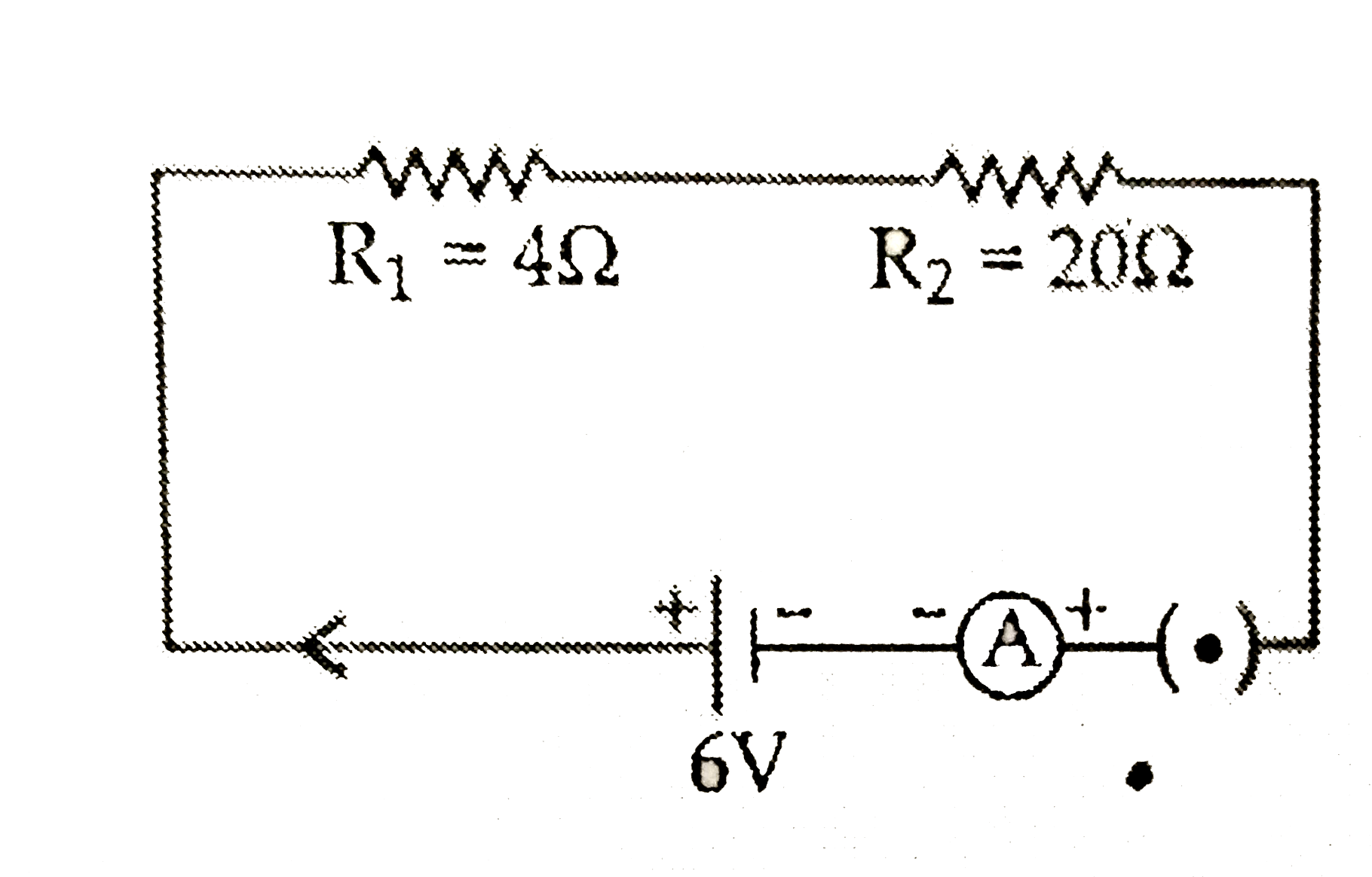
(a) the total resistance of the circuit,
(b) the current through the circuit, and
(c) the potential differences across R1andR2
View SolutionIf a 16Ωresistance and 12Ω inductive reactance are present in an a.c series circuit. Then the impedance of the circuit will be
View SolutionIn the L-R circuit as shown in figure, potential difference across the resistance at some instant is 4 V. Then
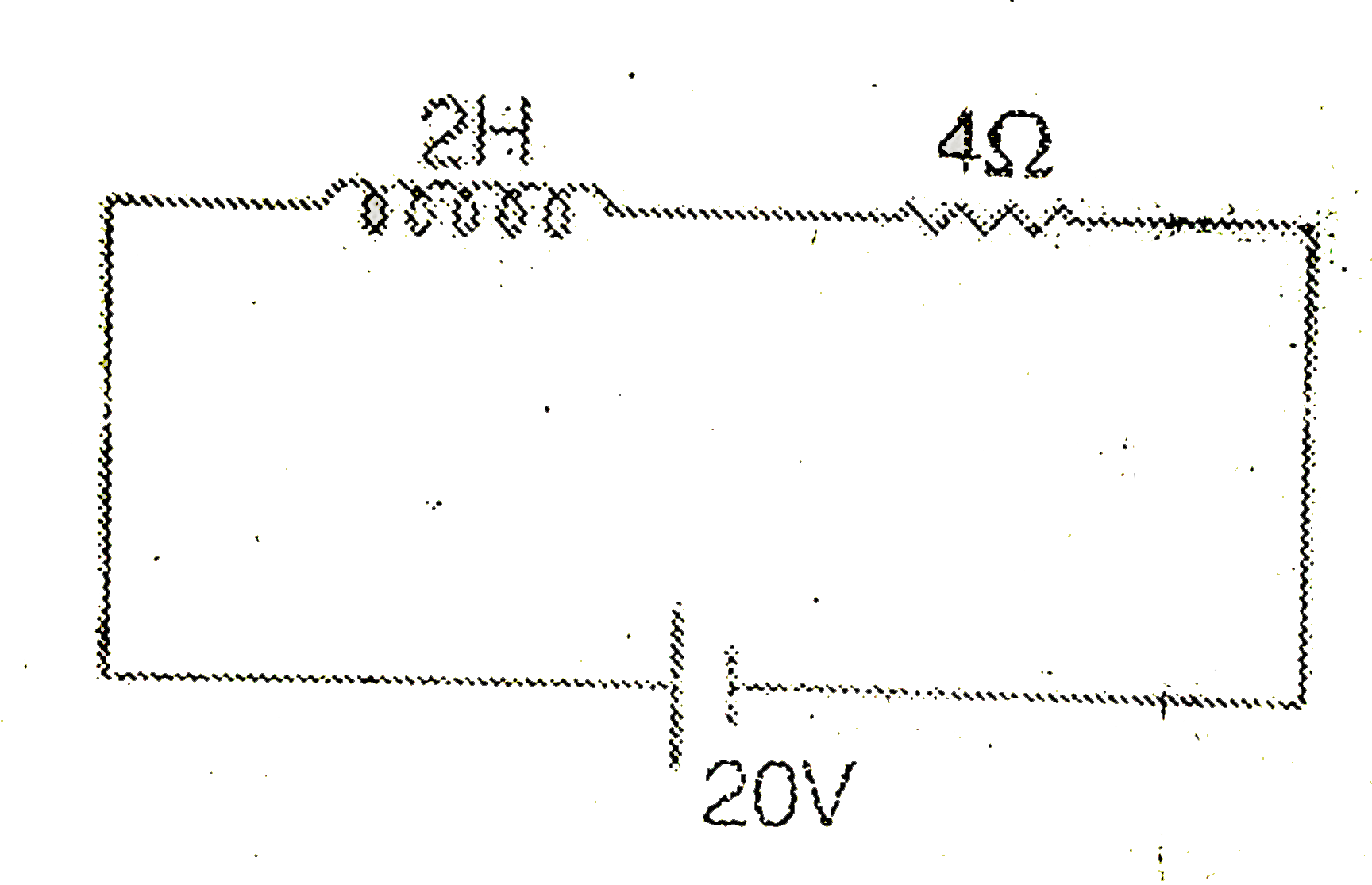
View SolutionThe frequency of oscillation of current in the indcutor is

View SolutionA resistor R an inductance L and a capacitor C are all connected in series with an ac supply The resistance of R is 16ohm and for the given frequency the inductive reactance of L is 24 ohm and the capacitive reactance of C is 12ohm If the current in the circuit is 5A find
(a) the potential difference across R,L and C
(b) the impedance of the circuit
(c) the voltage of the ac supply and
(d) the phase angle .
View Solutionin a series LCR circuit, what is the phase difference between VLandVC where VL is the potential difference across the inductor and VC is the potential difference across the capacitor?
View SolutionFor a series RLC circuit R=XL=2XC. The impedence of the current and phase different (between) V and i will be
View SolutionA circuit has a resistance of 11Ω, an inductive reactance of 25Ω, and a capacitive resistance of 18Ω. It is connected to an AC source of 260V and 50Hz. The current through the circuit (in amperes) is
View Solution

