Using the parallel axes theorem, find the M.I. of a sphere of mass m about an axis that touches it tangentially. Given that Icm=25mr2
To find the moment of inertia (M.I.) of a sphere of mass m about an axis that touches it tangentially using the parallel axes theorem, we can follow these steps:
Step 1: Identify the Moment of Inertia about the Center of Mass
The moment of inertia of a solid sphere about an axis through its center of mass is given by the formula:
Icm=25mr2
where r is the radius of the sphere.
Step 2: Apply the Parallel Axis Theorem
The parallel axis theorem states that if you want to find the moment of inertia about an axis parallel to an axis through the center of mass, you can use the formula:
I=Icm+md2
where:
- I is the moment of inertia about the new axis,
- Icm is the moment of inertia about the center of mass,
- m is the mass of the object,
- d is the distance between the two axes.
Step 3: Determine the Distance d
In this case, the distance d is equal to the radius r of the sphere since the tangential axis touches the sphere at its surface. Therefore, we have:
d=r
Step 4: Substitute Values into the Parallel Axis Theorem
Now, substituting the values into the parallel axis theorem:
I=Icm+md2
I=25mr2+m(r2)
I=25mr2+55mr2
I=25mr2+55mr2=75mr2
Step 5: Final Result
Thus, the moment of inertia of the sphere about the axis that touches it tangentially is:
I=75mr2
The moment of inertia of a solid sphere about an axis through its center of mass is given by the formula:
Icm=25mr2
where r is the radius of the sphere.
The parallel axis theorem states that if you want to find the moment of inertia about an axis parallel to an axis through the center of mass, you can use the formula:
I=Icm+md2
where:
- I is the moment of inertia about the new axis,
- Icm is the moment of inertia about the center of mass,
- m is the mass of the object,
- d is the distance between the two axes.
In this case, the distance d is equal to the radius r of the sphere since the tangential axis touches the sphere at its surface. Therefore, we have:
d=r
Now, substituting the values into the parallel axis theorem:
I=Icm+md2
I=25mr2+m(r2)
I=25mr2+55mr2
I=25mr2+55mr2=75mr2
Thus, the moment of inertia of the sphere about the axis that touches it tangentially is:
I=75mr2
Similar Questions
The M.I. of a ring of mass M and radius R about a tangential axis perpendicular to its plane is :
View SolutionThe moment of ineria (I) of a sphere of radius R and mass M is given by
View SolutionThe M.I. of a thin ring of mass M and radius R about an axis through the diameter in its plane will be:
View SolutionThe M.I. of a ring and disc of same mass and radius about their geometric axes will be:
View SolutionFind the moment of inertia of a uniform sphere of mass m and radius R about a tangent if the spheres (1) solid (ii) hollow?
View SolutionFind the volume of a sphere whose radius is(i) 7 cm (ii) 0.63 m
View SolutionUsing De Moivre's theorem, find the least positive integer n such that (2i1+i)n is a positive integer.
View SolutionUse the parallel axis theorem to find the moment of inertia ofa uniform rod of mass M = 3kg and length 2a (a = 1m), about a perpendicular axis through one end?
View Solution3 particles of mass 10 gm each are placed at the corners of an equilateral triangle of side 5 cm. The M.I. of the system about a perpendicular axis to the plane passing through a corner of the triangle will be : (in kg-m2)
View Solution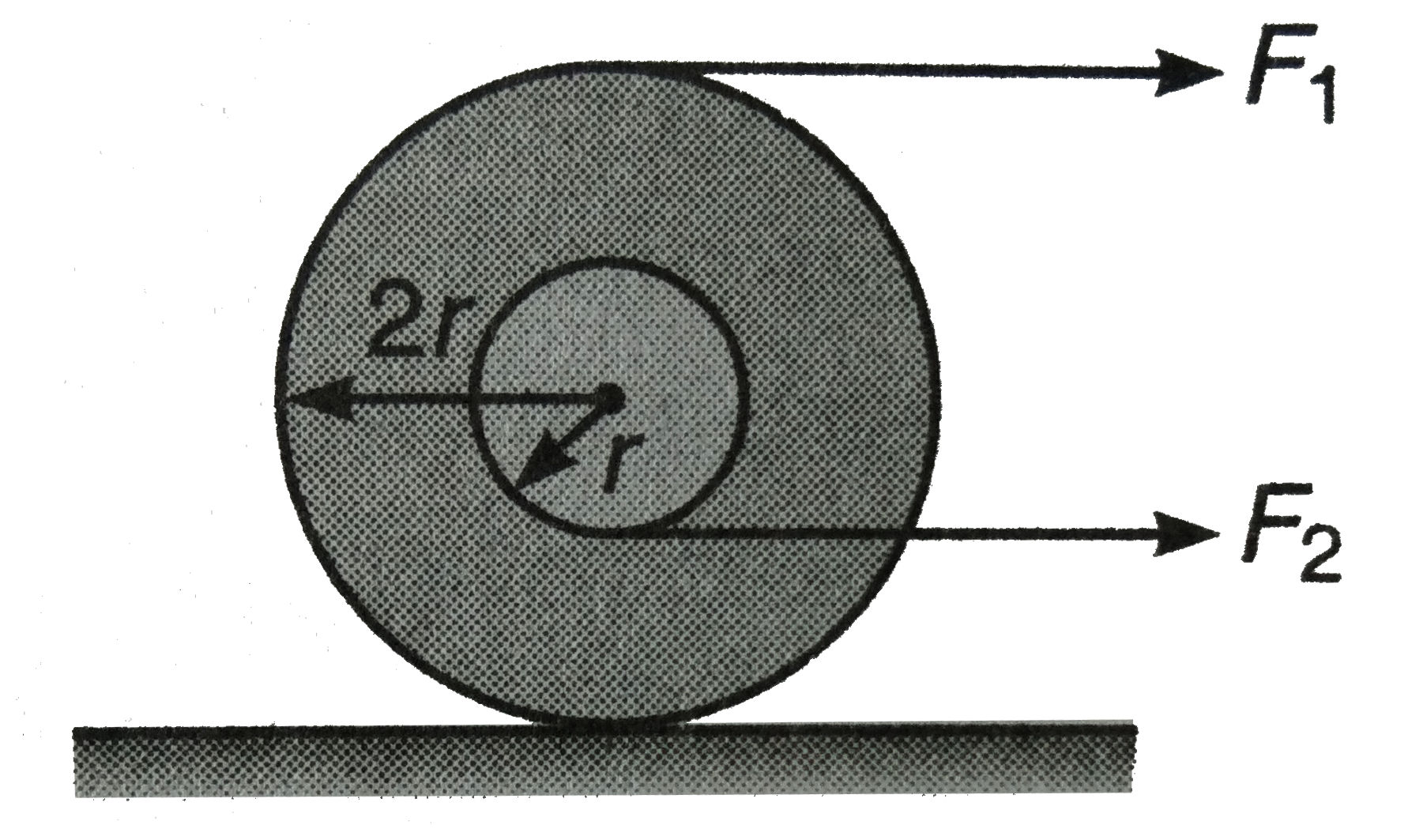
Two forces F1 and F2 are applied on a spool of mass M and moment of inertia I about an axis passing through its centre of mass. Find the ratio F1F2. So that the force of friction is zero. Given that I<2Mr2.
View Solution
