The magnitude of the gravitational field at distance r1 and r2 from the centre of a uniform, sphere of radius R and mass M are F1 and F2 respectively then-
Gravitational field intensity for a uniform spherical distribution of mass is given by :
l=GMr2 for r>R and I=GMR3r for r<R.
(a)r1>R and r2>R
l2l2=(GM/r21)(GM/r22)=r22r21
(b)r1<R and r2<R
l1l2=(Gm/R3)r1(GM/R3)r2=r1r2
(c)r1>R and r2<R
l1l2=(GM/r21)(GM/R3)r2=R3r21r2
Similar Questions
The magnitude of the gravitational field at distance r1andr_2omthecentreofaunifromsphereofradiusRandmassmareF_1 and F_2 respectively. Then:
View SolutionThe magnitude of gravitational field at distances r1 and r2 from the centre of a uniform sphere of radius R and mass M, respectively. Find the ratio of (I1)/(I2)) if r1>R and r2>R.
View Solution
Knowledge Check
The correct plot of the magnitude of magnetic field →B vs distance r from centre of the wire is, if the radius of wire is R
A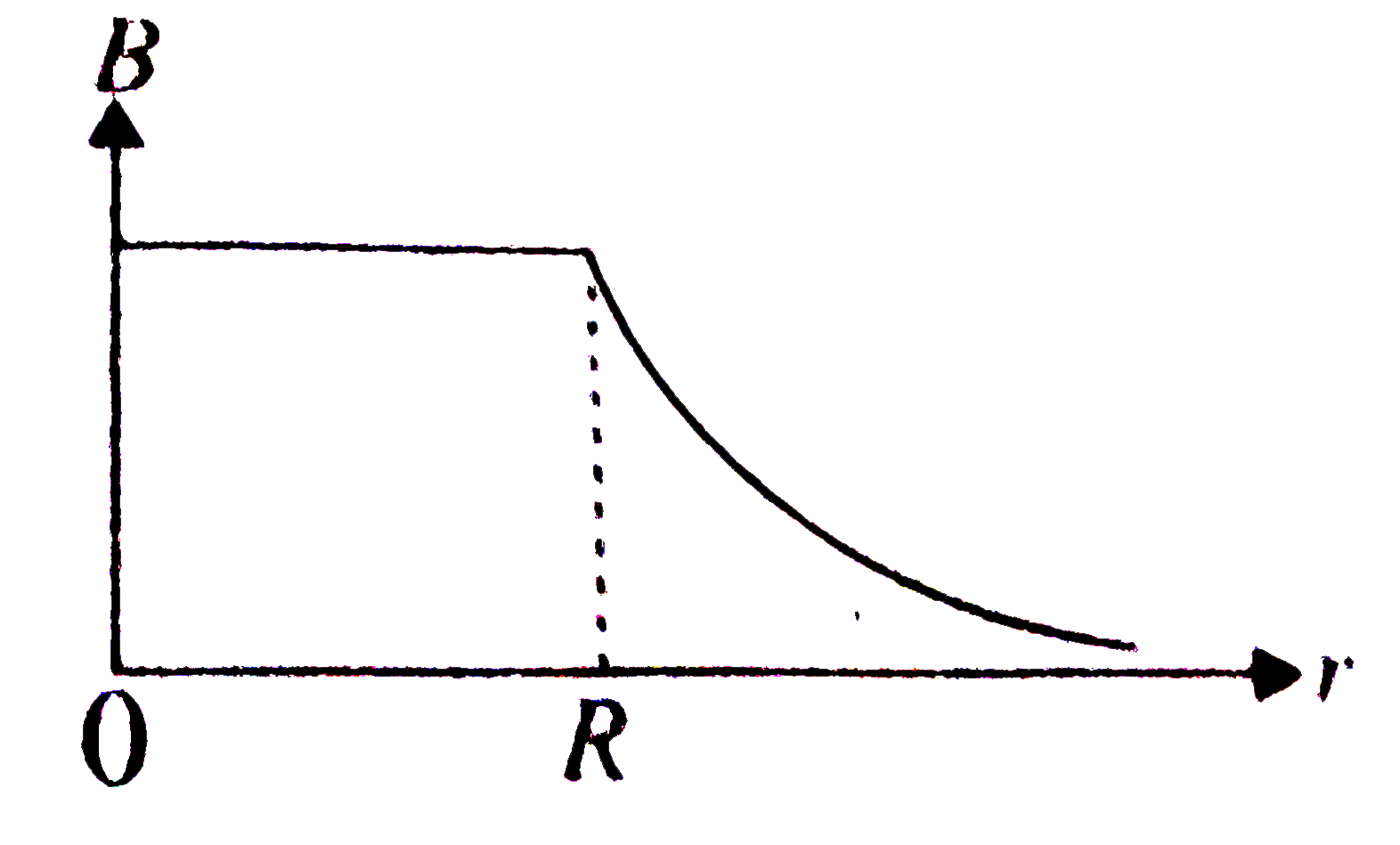 B
B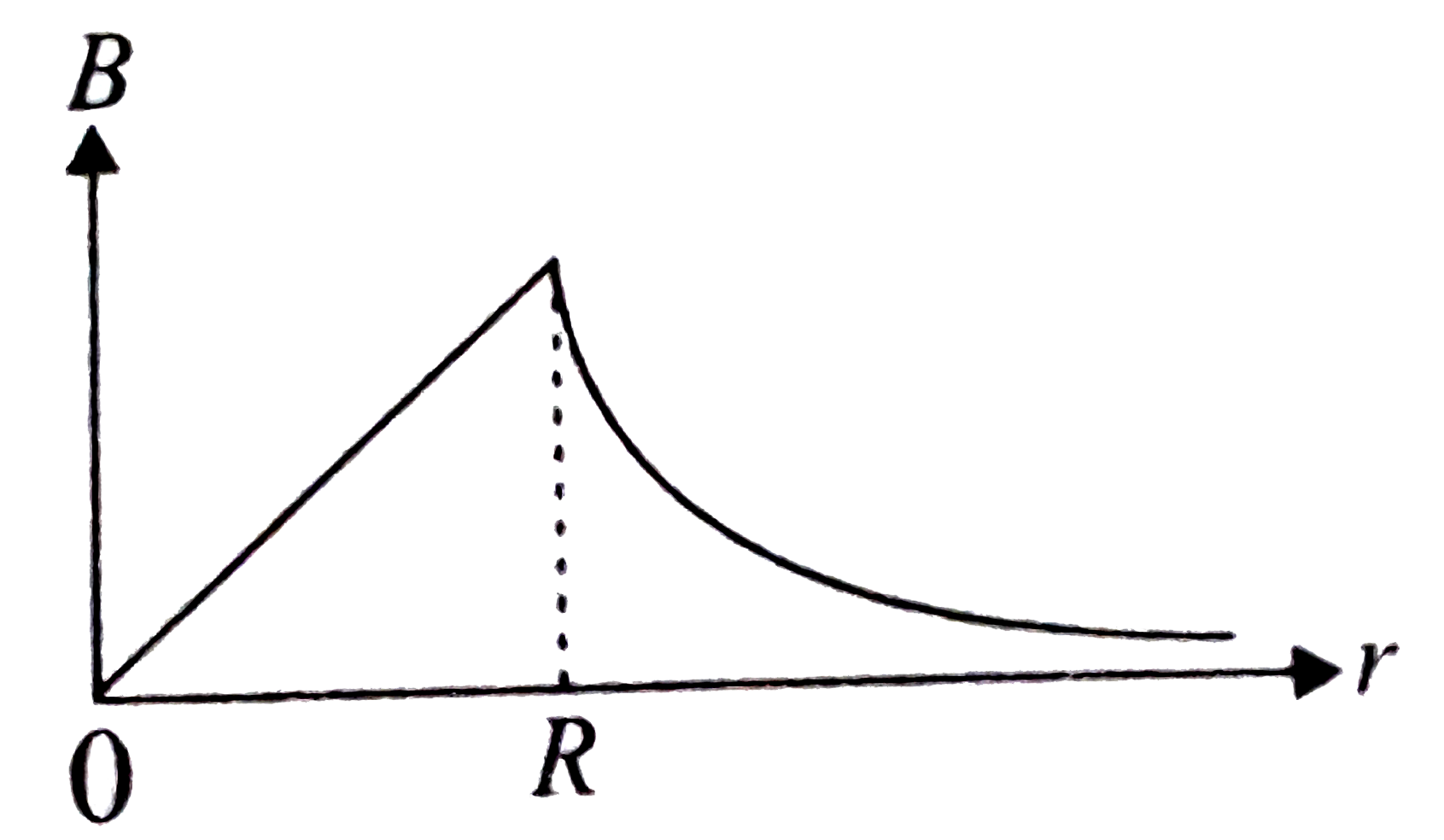 C
C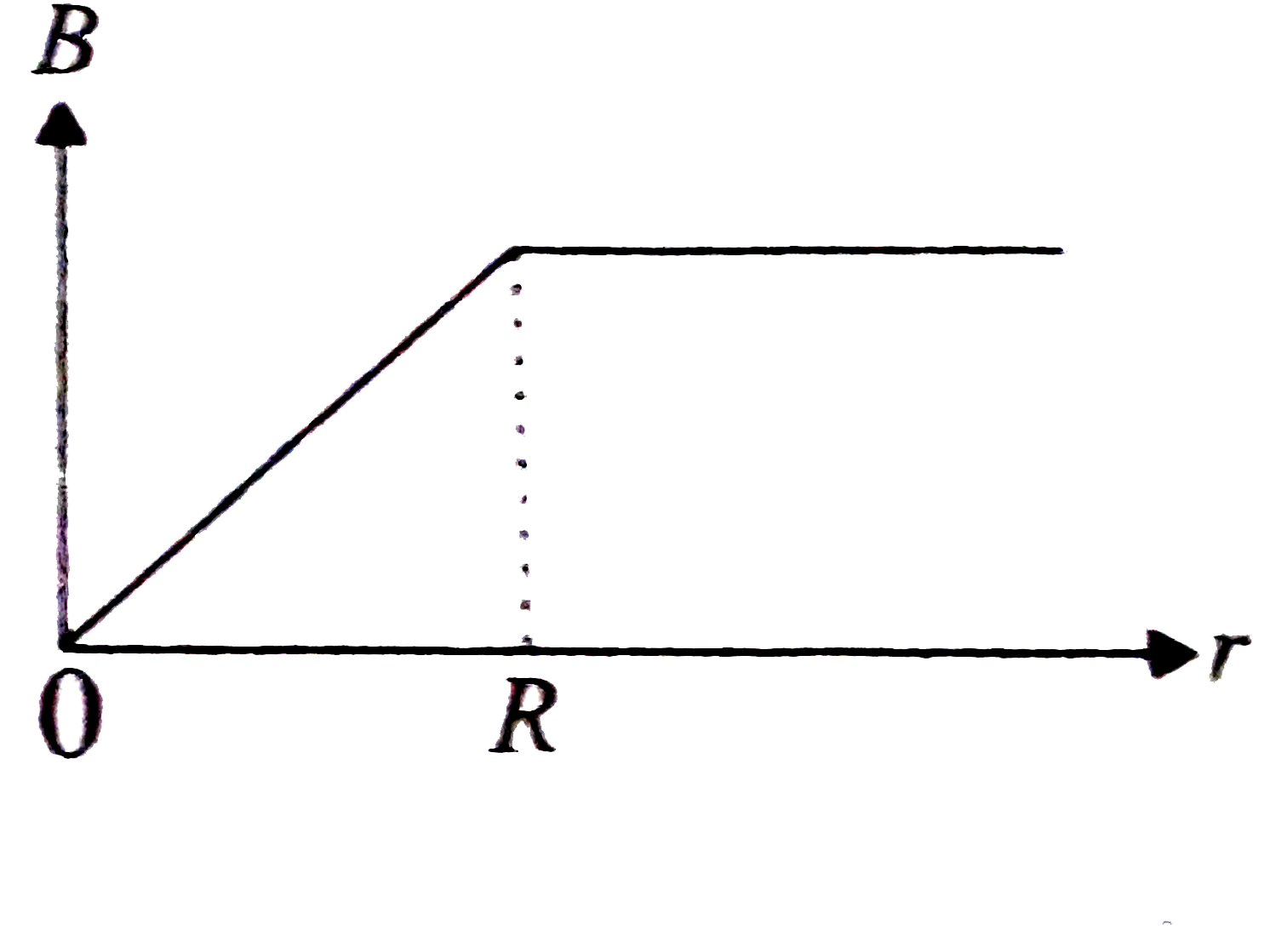 D
D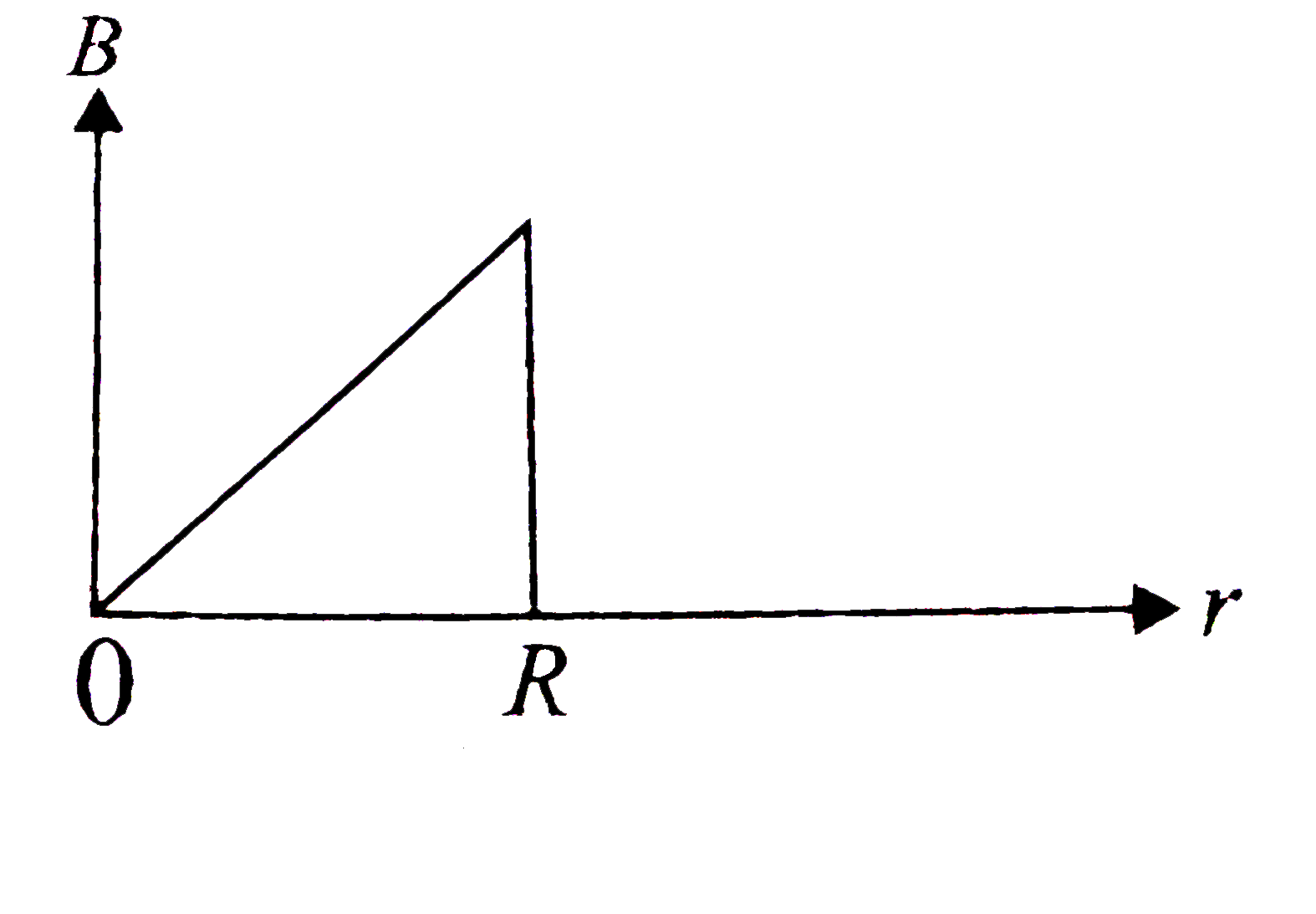
The gravitational potential energy of a body at a distance r from the centre of earth is U. Its weight at a distance 2r from the centre of earth is
View SolutionLet V and E represent the gravitational potential and field at a distance r from the centre of a uniform solid sphere. Consider the two statements.
A. the plot of V agasinst r is discotinuous
B. The plot of E against r is discontinuous.
View SolutionFigure shows variation of acceleration due to gravity with distance from centre of a uniform spherical planet, Radius of planet is R. What is r1−r1
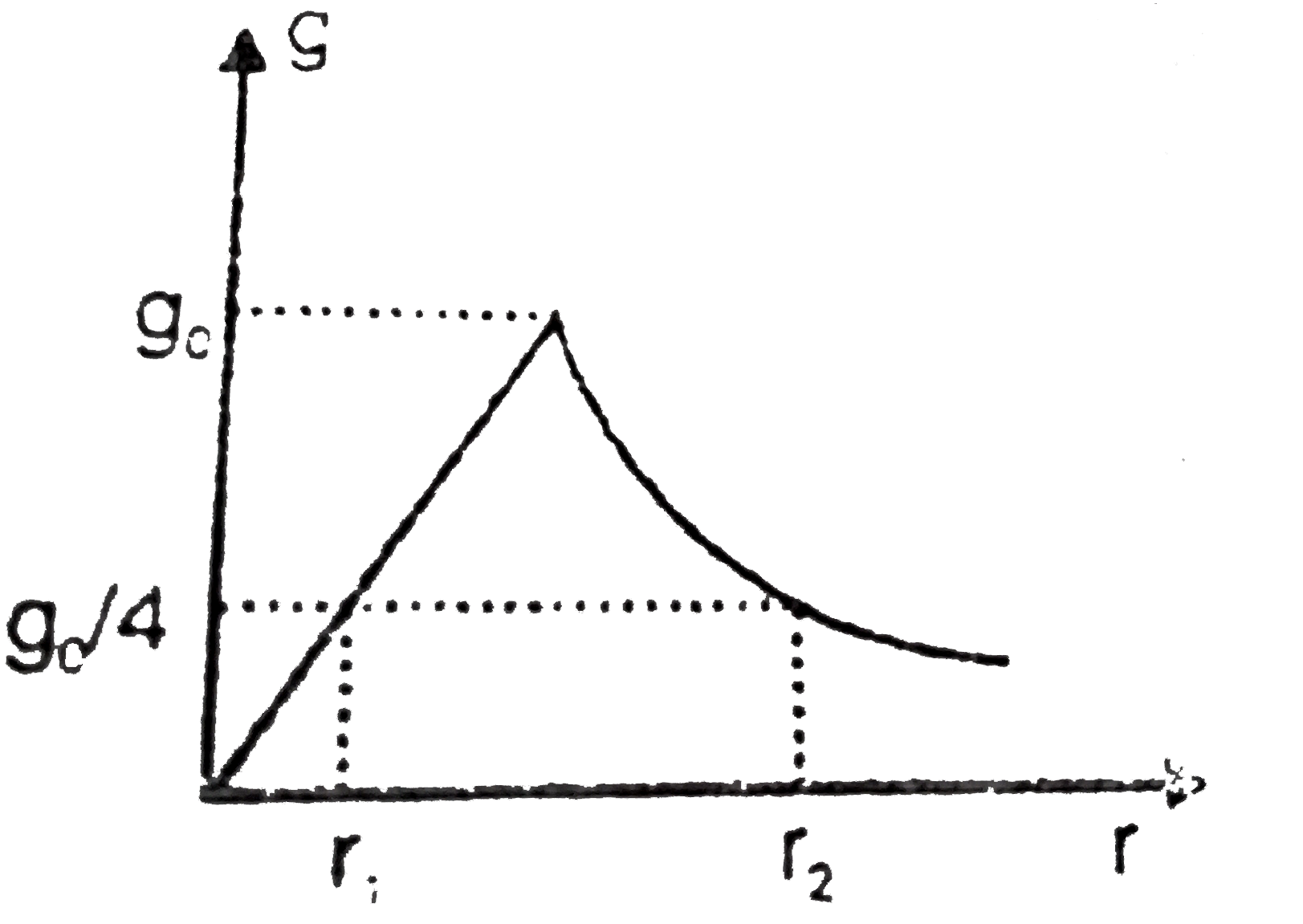
View SolutionThe gravitational field due to an uniform solid sphere of mass M and radius a at the centre of the sphere is
View SolutionFollowing curve shows the variation of intesity of gravitational field (→I) with distance from the centre of solid sphere(r) :
View SolutionThe gravitational potential at a point outside the solid sphere of radius "R" and at a distance of "r" will be :
View SolutionA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R/2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM/R2, where M is the mass of the solide sphere]
View Solution
