The block of mass M in figure −4.160, initially has a velocity vo to the right and its positionis much that the spring exerts no froce on it, i.e, the spring is not stretched or comkpressed. The block moves to the right a distance l before sttoping in the dotted position shown. The speing constant is k and the coefficeent of kinetic friction between block and table is μ. as the block moves the distance l, (a) what is the work done on it by the friction force ? (b) What is the work done on it by the spring force ? (c) are there other forces actionon the block, and if so what work do they do ? (d) what is the total work done on the block?
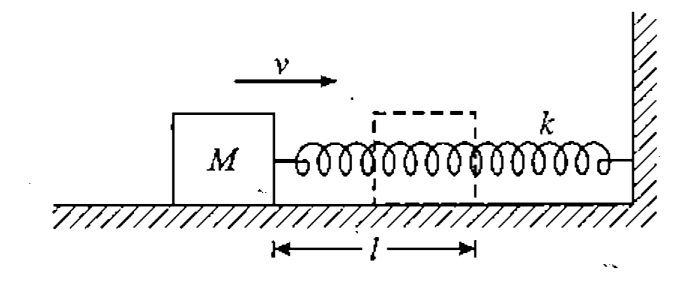
(a) The net force acting on the block by the spring is equal to Fspring=kx
Work done by the spring =∫→Fspring.d→s
=∫Fspringdscos180∘=−∫Fspring.ds
=−∫l0kxdx=−kl22
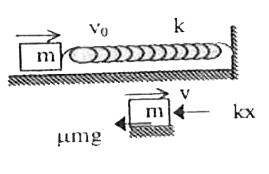
(b) The total work done W=ΔKE=0−(12)mv20=−(12)mv20.
(c) The work done by friction =−μmgl
⇒ The total work done Ws+Wf=ΔKE=−μmgl−(1/2)kl2=−(12)mv20
⇒12kl2+μmgl=12mv20
⇒l=μmgk⎡⎣√1+km(v0μg)2−1⎤⎦
Similar Questions
A block of mass m slides in right angled incliine through as shown in the figure . If the coefficient of kinetic friction between the block and the through is μk , find the acceleration of the block .

View SolutionA block of mass m is moving on a rough horizontal surface. μ is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
View SolutionA block of mass m sides down an inclined right angled trough .If the coefficient of friction between block and the trough is μk acceleration of the block down the plane is

View SolutionA block of mass m has initial velocity u having direction towards +x axis. The block stops after covering a distnce S causing similar extension in the spring of constant K holding it. If μ is the kinetic friction between the block and the surface on which it was moving, the distance S is given
View SolutionA block of mass m moving at a speed v compresses a spring throgh a distance x before its speed is halved. Find the spring constant of the spring.
View SolutionA block of mass m moving at a speed 'v' compresses as spring through a distance 'x' before its speed is halved. Find the spring constant of the spring.
View SolutionA block of mass m is pressed against a wall by a spring as shown in the figure. The spring has natural length , l(l>L), and the coefficient of friction between the block and the wall is μ . The minimum spring constant K necessary for equilibrium is:
View SolutionA block of mass 2.0 kg is given an initial speed along the floor towards a spring as shown. The coefficient of kinetic friction between the floor and the block is 0.4 and force constant of the spring is 5.6×103 N/m. The block compresses the spring by 10cm before it stops for a moment. What is the initial speed (m/s) of the block?
View SolutionA block of mass m is connected with a rigid wall by light spring of stiffness k. Initially the spring is relaxed.

If the block is pushed with a velocity v0, it oscillates back and forth and stops. Assuming μ as the coefficient of kinetic friction between block and ground, find the work done by friction till the block stops.
View SolutionIn the system as shown in figure, the blocks have masses m1 and m2, the spring constant is k, coefficient of friction between the block of mass m1 and the surface is μ. The system is released with zero initial speed from the position where the spring is in its natural length.

View Solution
