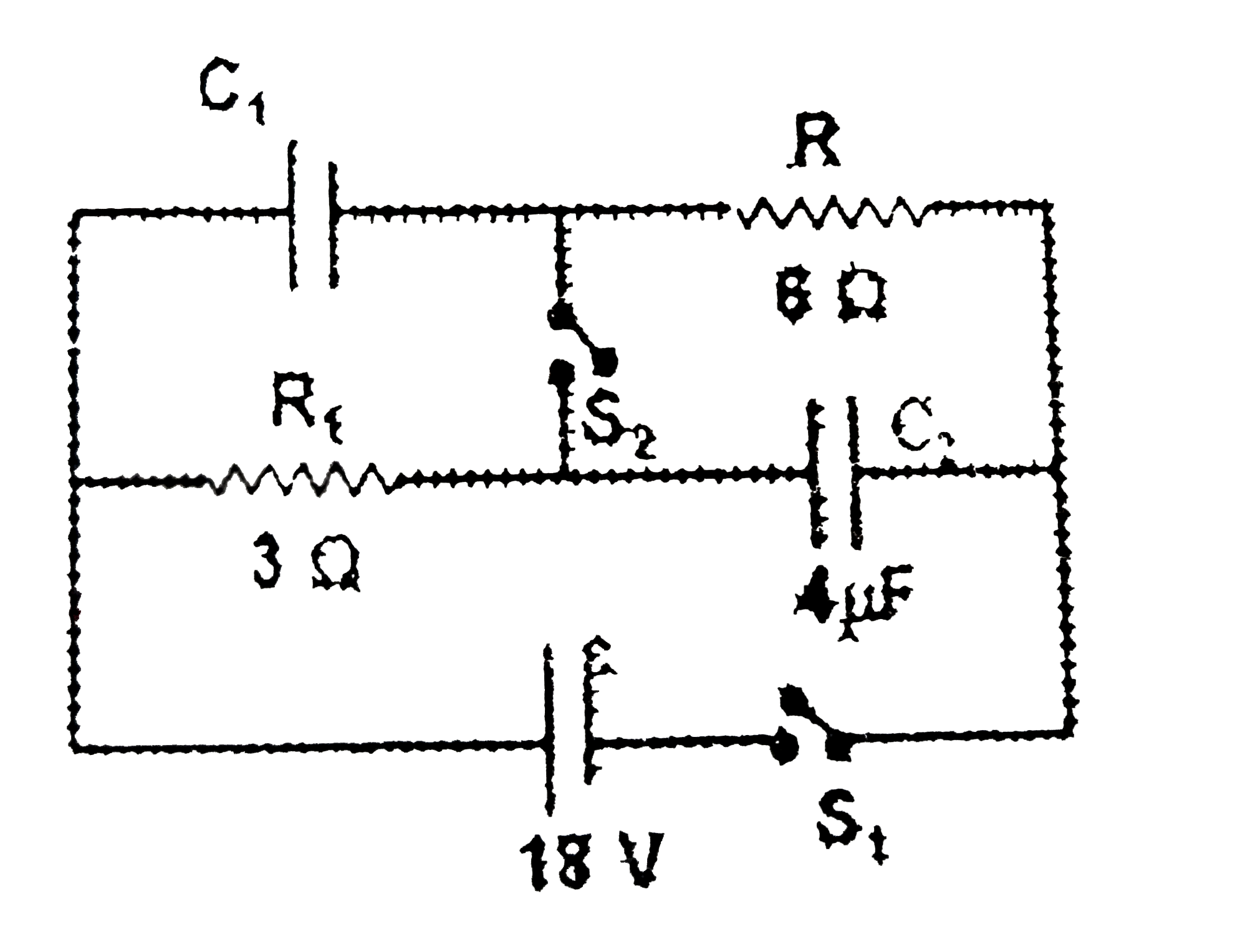
Consider the shown network. Initially both swiches are open and the capacitor are uncharged. Both the switches are then closed simultaneously at t=0
(a) Obtain the current through switch S2 as function of time.
(b) If switch S2 is opened again after a long time interval, find the total heat that would dissipate in the resistor and the charge that would flow through switch S1 after S2 is opened?
Consider the charges on capacitors and currents through various branches, as shown in the figure
For loop 1, we have
R1(I2+I3−I1)=q1C1 (1)
For loop2, R2i3=q2C1 (2)
For the outer loop, i3R2+q1C1=ε (3)
Also, i1=dq1dt and i2=dq2dt (4)
Putting the values of i1 and i2 from Eq. (4) and of i3 from Eq. (2) in (1), we get
ddt(q2−q1)=q1R1C1−q2R2−C2 (5)
From Eqs. (2) and (3), we get
q2C2+q1C1=ε (6)
From Eqs. (5) and (6), we get
∫q20dq2(εC2R2R1+R2)−q2=∫t0dtReq(C1+C2), where Req=R1R2R1+R2
⇒q2=εR2C2(R1+R2)[1−e1Req(C1+C2)]
Similarly, q1=εR1C1(R1+R2)[1−e1Req(C1+C2)]
⇒i1=dq1dt=εC1R2(C1+C2)e1Req(C1+C2)
Similarly, i2=εC2R1(C1+C2)e−1Req(C1+C2)
From equation (1)
Current through S2=(i1−i3)=i2−q1R1C1
Putting the values, we get
q1=(12μC)(1−e112μ), q2=(48μC)(1−e112μ)
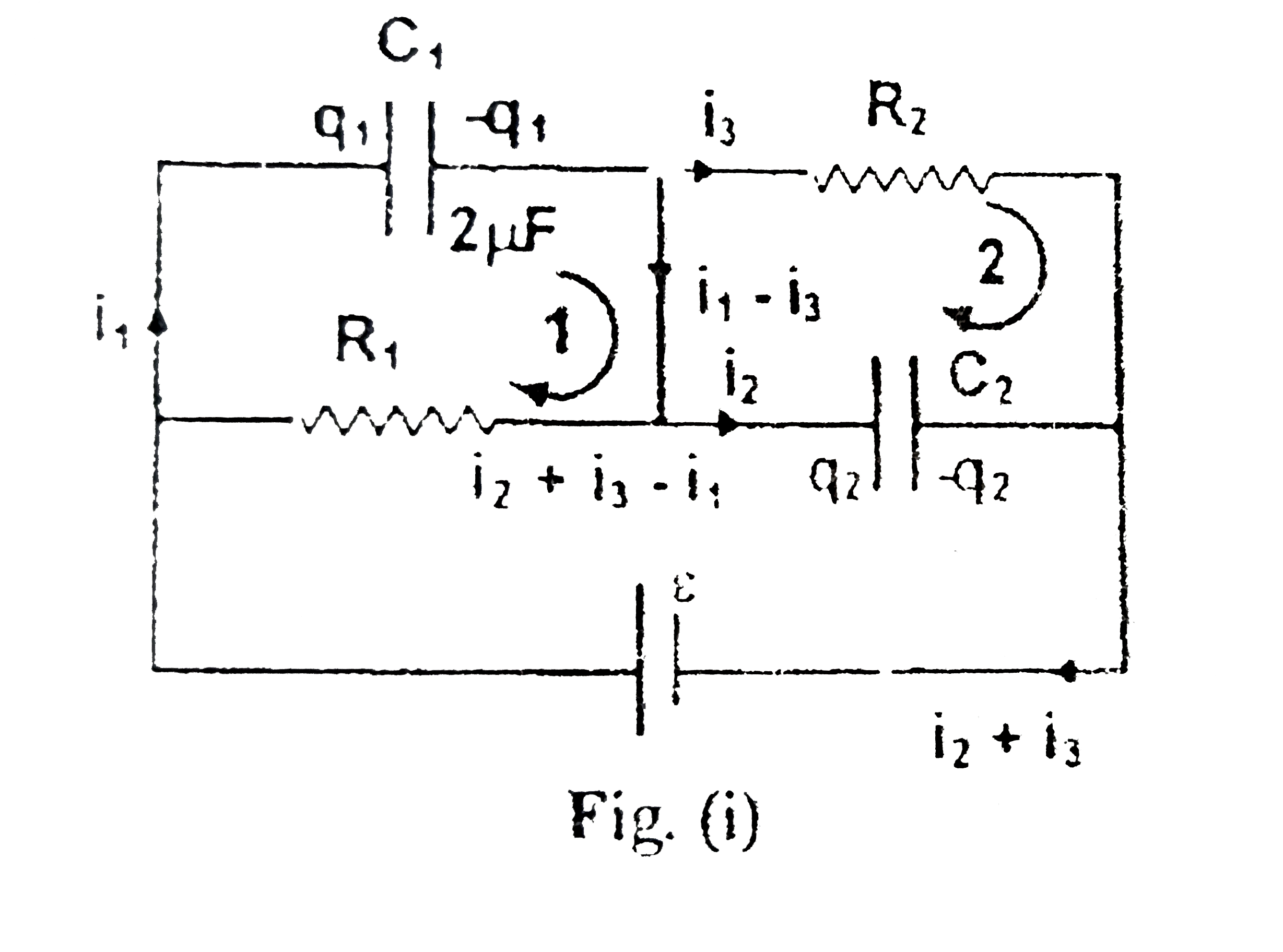
i1=(1A)e112μ, i2=(4A)e112μ
Current through switch s2=−[2−e112μ]A along the indicated direction as shown in fig (i),
With both the switches closed the steady state charges and currents are as shown in Fig (ii).
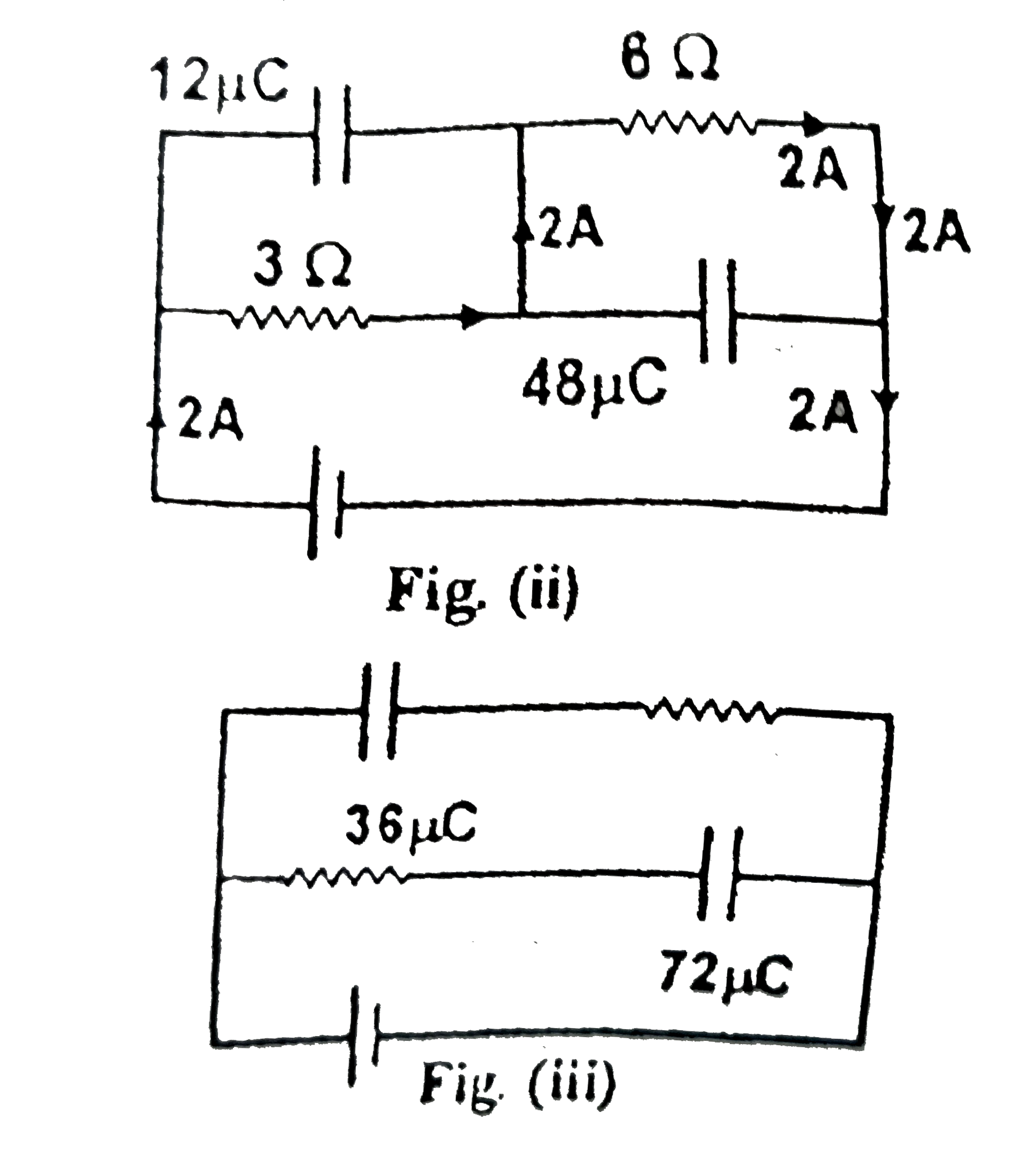
With switch S2 open and s1 closed, the steady state charges are as shown in Fig.(iii).
Hence, the charge flown through switch S1=[(36+72)−(12+48)]μC=48μC.
Total heat dissipated in the resistors = [Initial energy + work done by battery when 48μC flows through it after switch S2 is opened ] − [final energy]
={12C1V21+12C2V22}+ε(ΔQ)−{12C1V'21+12C2V'22}=136μJ.
Similar Questions
In the circuit shown, switch S is closed at time t=0. Find the current through the inductor as a function of time t.

View SolutionThe flow of charge through switch S if it is closed is
View SolutionIn Fig. switch S is closed for a long time. At t=0, if it is opened, then

View SolutionIn Fig. switch S is closed for a long time. At t=0, if it is opened, then

View Solution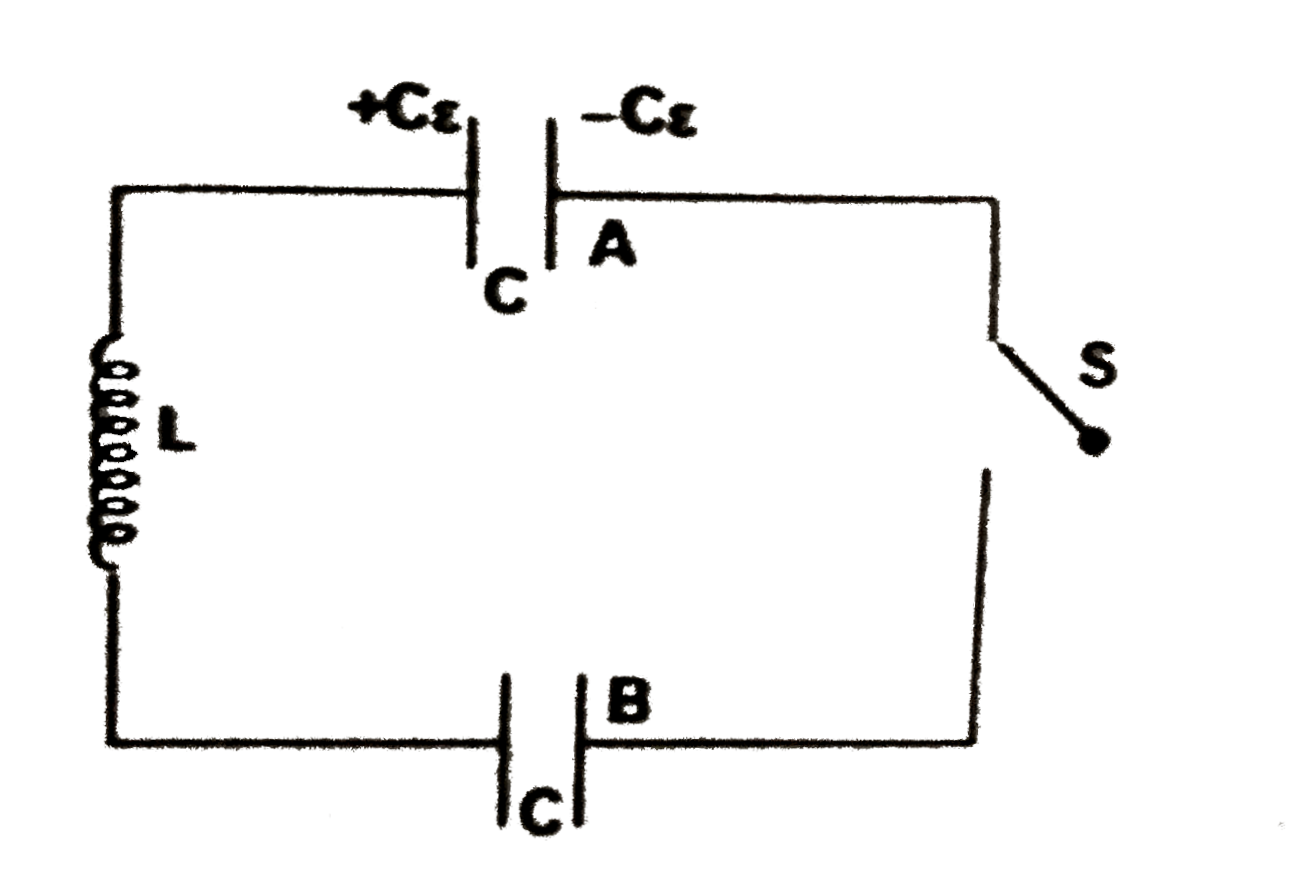
Initially capacitor 'A' is charged to a potential drop ε and capacitor B is uncharged At t=0, switch S is closed, then the maximum current through the inductor is
View SolutionThe switch in figure is closed at time t=0. Find the current in the inductor and the current through the switch as functions of time thereafter.
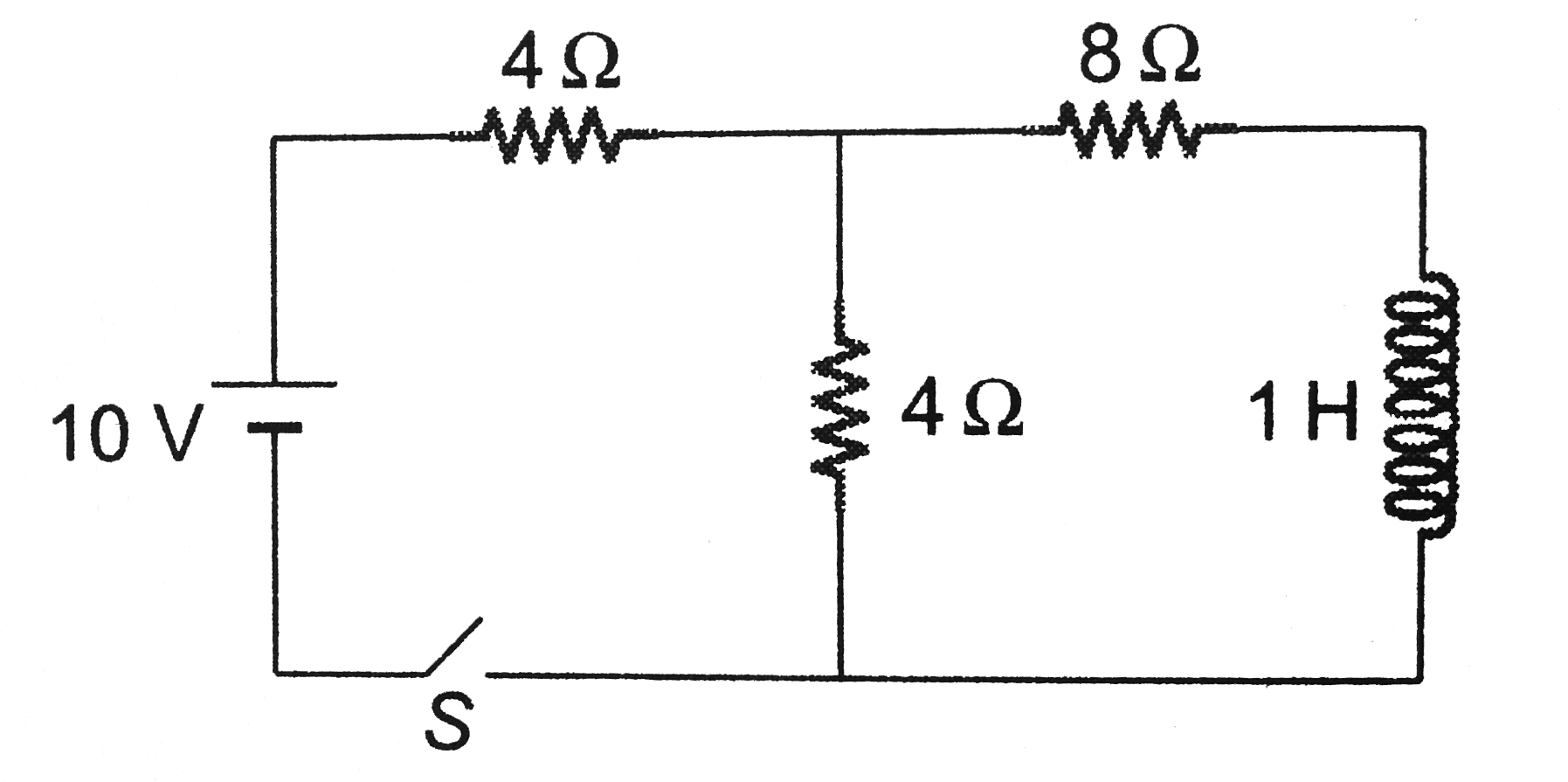
View SolutionInitially the capacitor is uncharged find the charge on capacitor as a function of time, if switch is closed at t=0.

View SolutionThe circuit was in the shown state for a long time. Now if the switch S is closed then the net charge that flows through the switch S, will be

View SolutionConsider the circuit shown in figure, after switch S is closed.

What amount of charge will flow through the switch?
View SolutionDetermine the current through the battery in the circuit shown in figure.
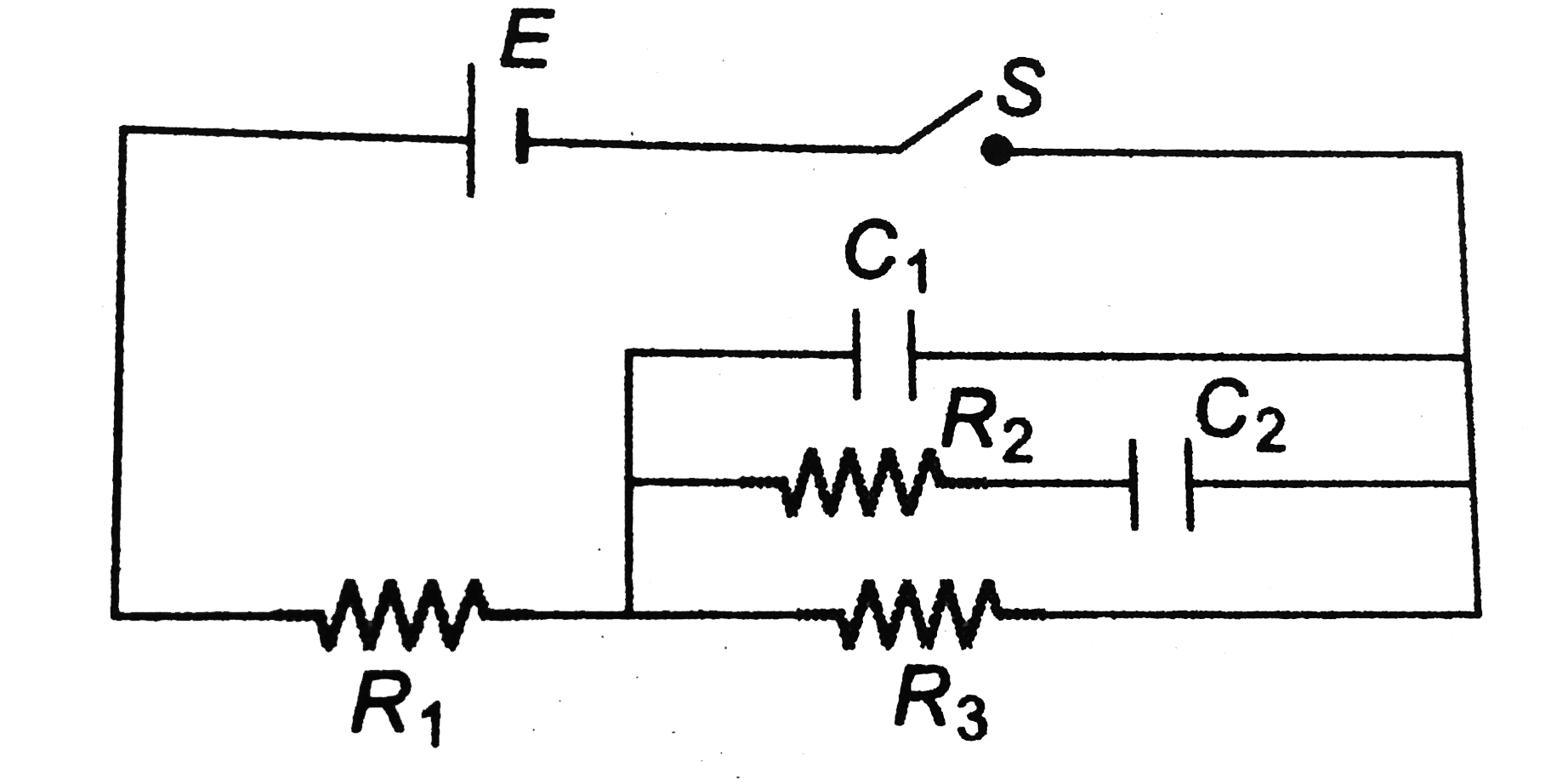
(a) immediately after the switch S is closed
(b) after a long time.
View Solution
