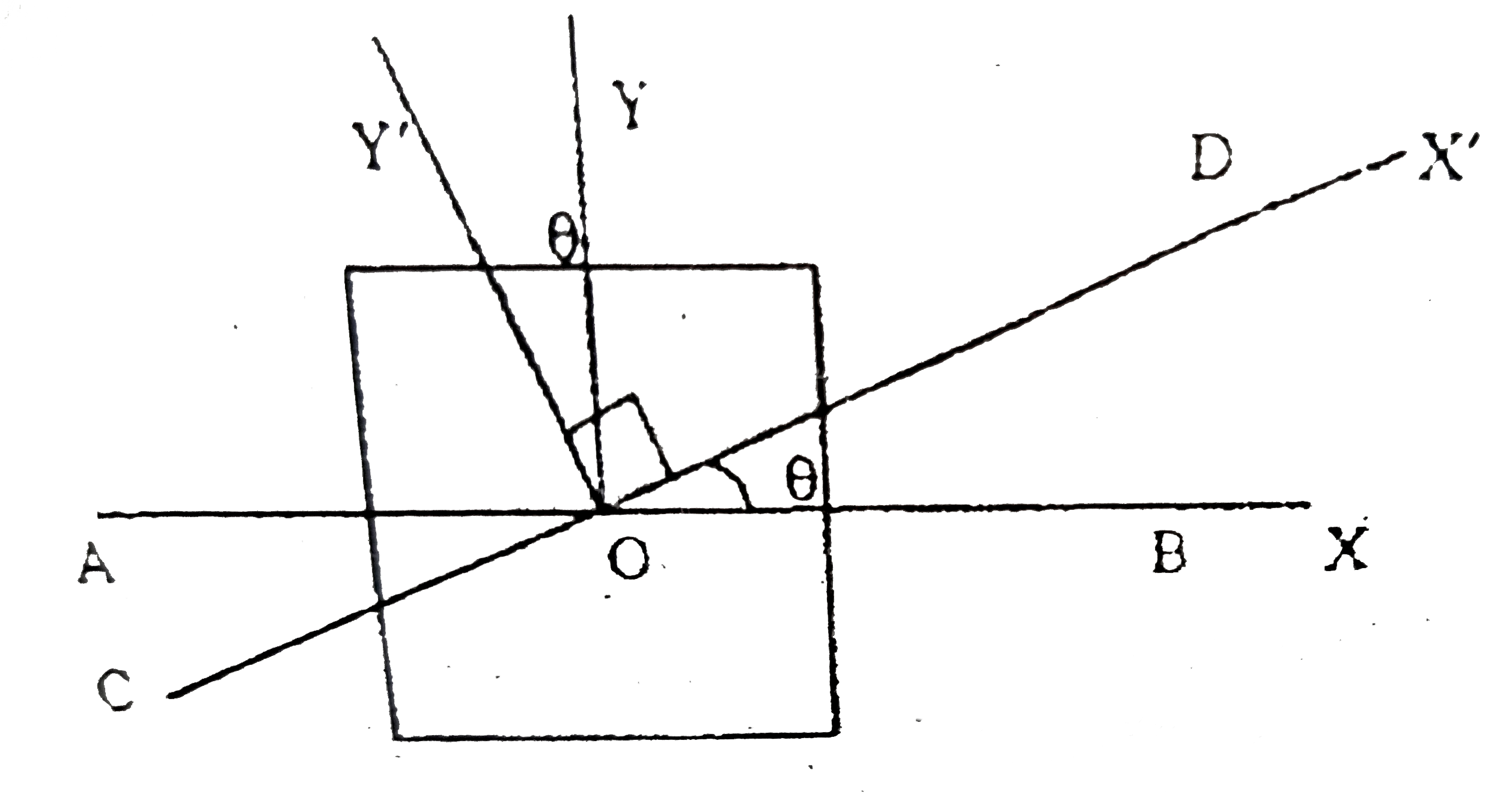
Let I be the moment of inertia of a uniform square plate about an axis AB that passes through its centre and is parallel to two of its sides. CD is a line in the plane of the plate that passes through the centre of the plate and makes an angle $θ$ with AB. The moment of inertia of the plate about the axis CD is then equal to

$I$

$I {cos}^{2} θ$

$I {sin}^{2} θ$

$I {cos}^{2} (θ / 2)$

Video Solution

Text Solution

Verified by Experts

According to the perpendicular axis theorem
$I_{z} = I_{x} + I_{y}$
Since the plate is quite-symmetrical about $x'$ and $y'$ , $I_{x'} = I_{y'}$
$\Rightarrow I_{z} = I'_{x} + I'_{y} = 2 I'_{x} = 2 I'_{y}$
$\Rightarrow I'_{x} = I'_{y} = I_{z} / 2$
Similarly, $I_{x} = I_{y} = I_{z} / 2$
$∴$ The required $M . I . = I$
where $\frac{I_{z}}{2} = I$

Updated on:21/07/2023

Ler l be the moment of inertia of a uniform square plate about an axis AB that passes through its centre and is parallel to two of its sides. CD is a line in the plane of the plate that passes through the centre of the plate and makes an angle $θ$ with AB. The moment of inertia of the plate about the axis CD is then equal to
A $I$
B $I {sin}^{2} θ$
C $I {cos}^{2} θ$
D $I {cos}^{2} (\frac{θ}{2})$ .