Two uniform solid cylinders A and B each of mass 1 kg are connected by a spring of constant 200Nm−1 at their axles and are placed on a fixed wedge as shown in fig.There is no friction between cylinders and wedge. The angle made by the line AB with the horizontal, in equilibirum is

0∘
15∘
30∘
None of these
In equilibrium, there will not be any friction between the cylinder and the wedge. If θ be the required angle
Cylinder A:mgsin60∘=kxcos(60∘−θ)(−mgcos30∘)
Cylinder B:mgsin30∘=kxcos(30∘+θ)=kxsin(60∘−θ)
∴cot30∘=cot(60∘−θ)⇒θ=30∘.
Similar Questions
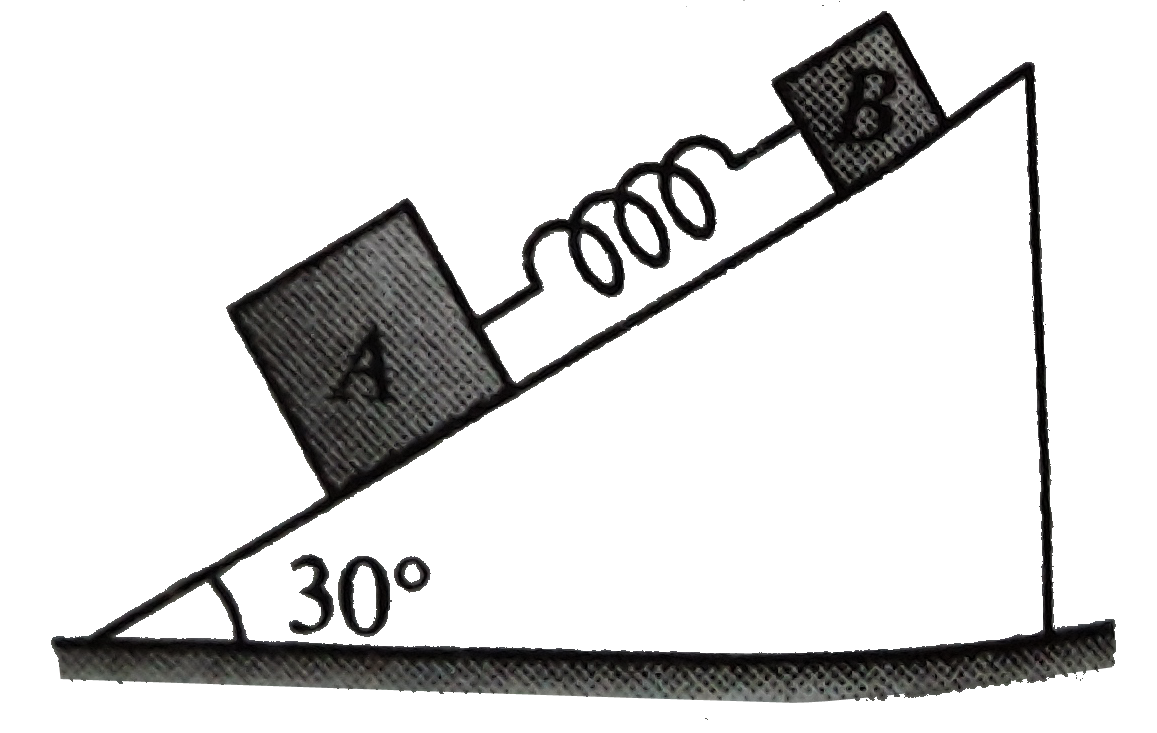
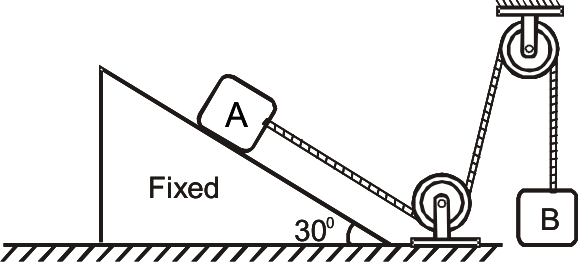
Two blocks A and B of masses 5kg and 2kg respectively connected by a spring of force constant =100Nm−1 are placed on an inclined plane of inclined 30∘ as shown in figure If the system is released from rest
View SolutionTwo identical blocks A and B, each of mass m=2kg are connected to the ends of an ideal spring having force constant K=1000Nm−1. System of these blocks and spring is placed on a rough floor. Coefficient of friction between blocks and floor is m=0.5. Block B is passed towards left so that spring gets compressed.
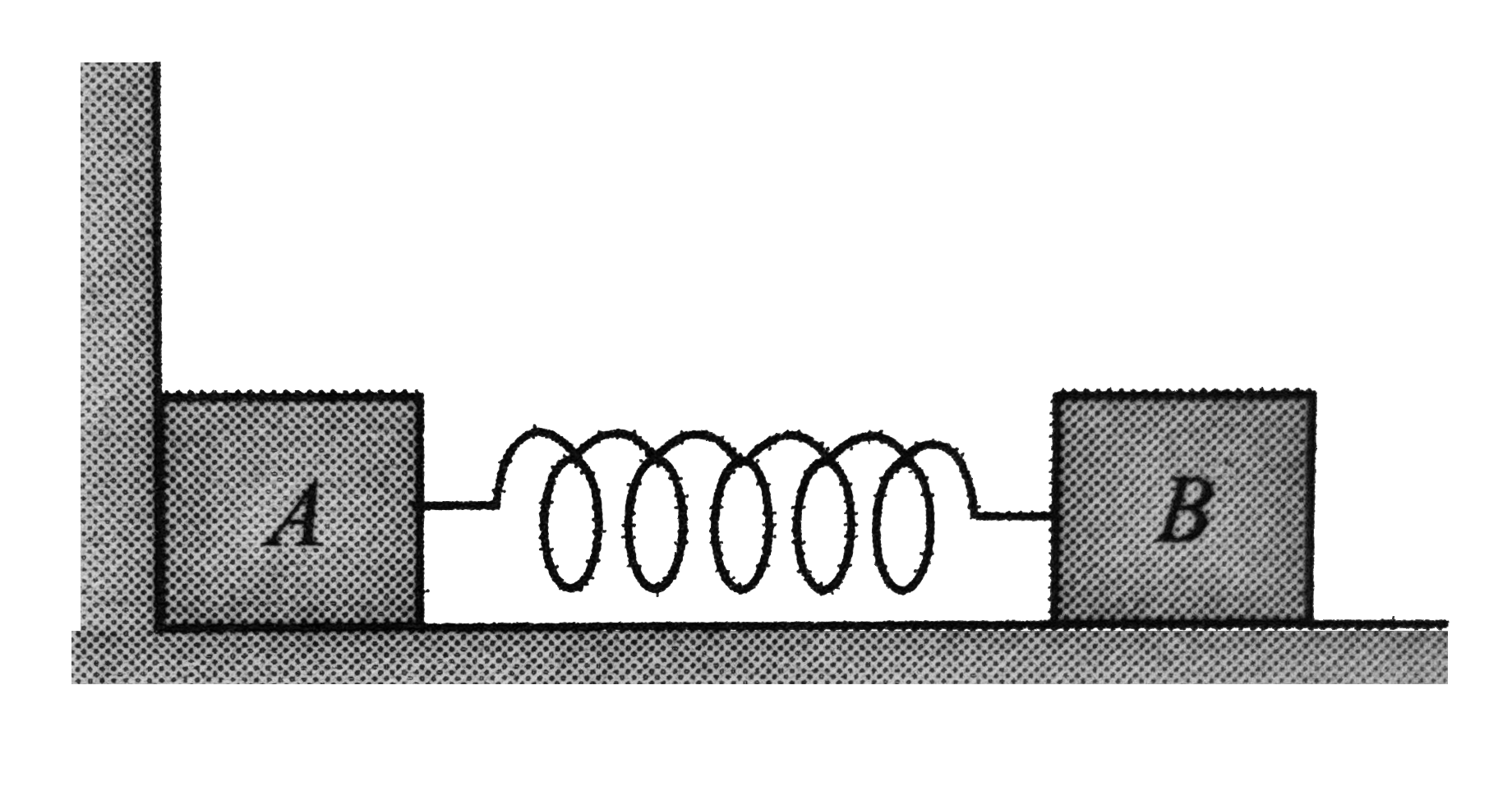
Calculate initial minimum compression x0 of spring such that block A leaves contact with the wall when system is released.
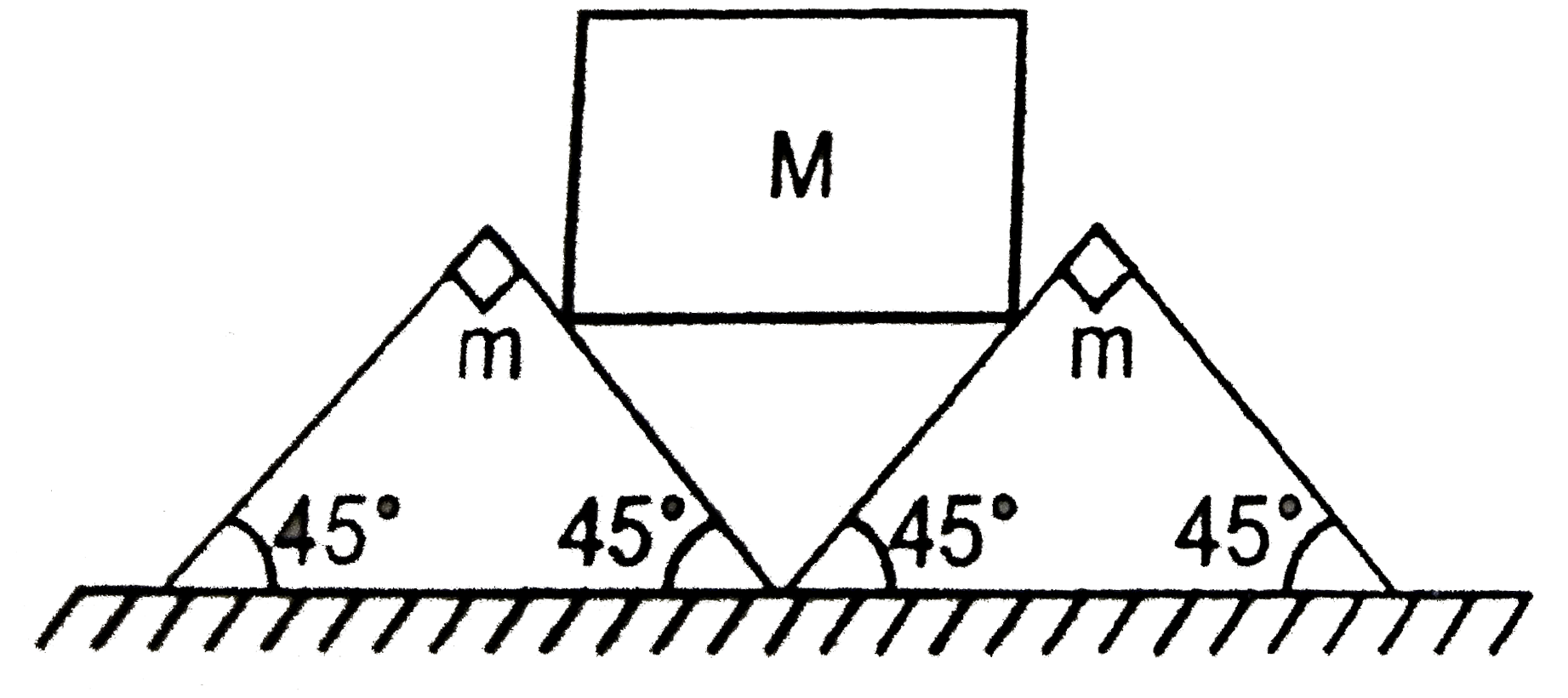
View SolutionTwo wedges, each of mass m, are placed next to each other on a flat horizontal floor. A cube of mass M is balanced on the wedges as shown in figure. Assume no friction between the cube and the wedges, but a coefficent of static friction μ<1 between the wedges and the floor. What is the largest M that can be balanced as shown without motion of the wedges ?
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10 cm, then maximum speed of the trolley is
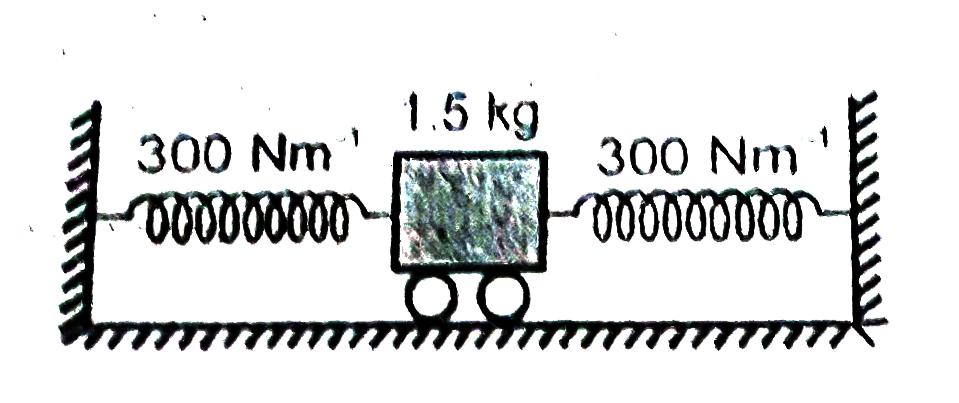
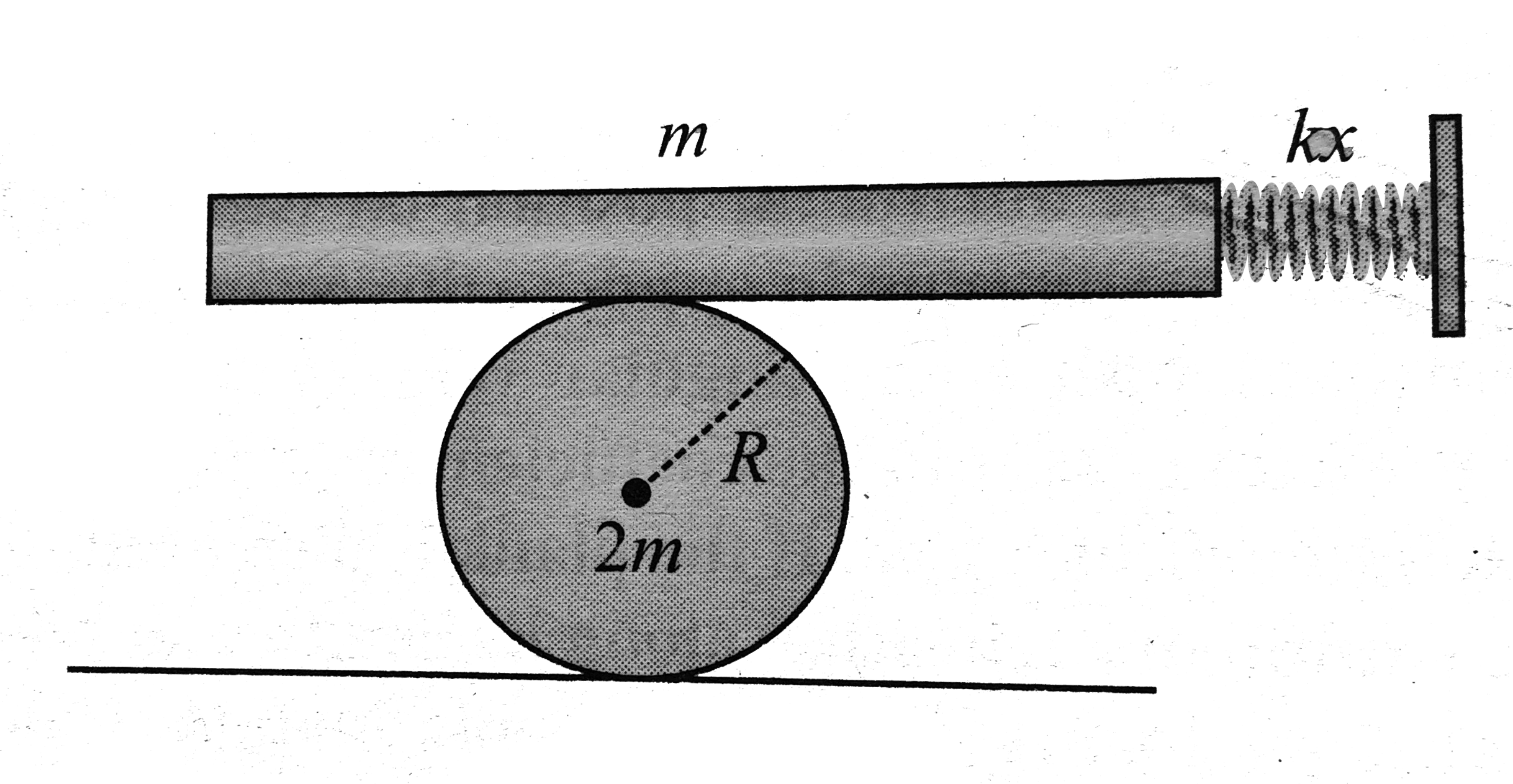
View SolutionA uniform plank of mass m, free to move in the horizontal direction only , is placed at the top of a solid cylinder of mass 2m and radius R. The plank is attached to a fixed wall by mean of a light spring constant k. There is no slipping between the cylinder and the planck , and between the cylinder and the ground. Find the time period of small oscillation of the system.
View SolutionA uniform solid. cylinder A of mass can freely rotate about a horizontal axis fixed to a mount of mass m2. A constant horizontal force F is applied to the end K of a light thread tightly wound on the cylinder. The friction between the mount and the supporting horizontal plane is assumed to be absent. Find the acceleration of the point K.
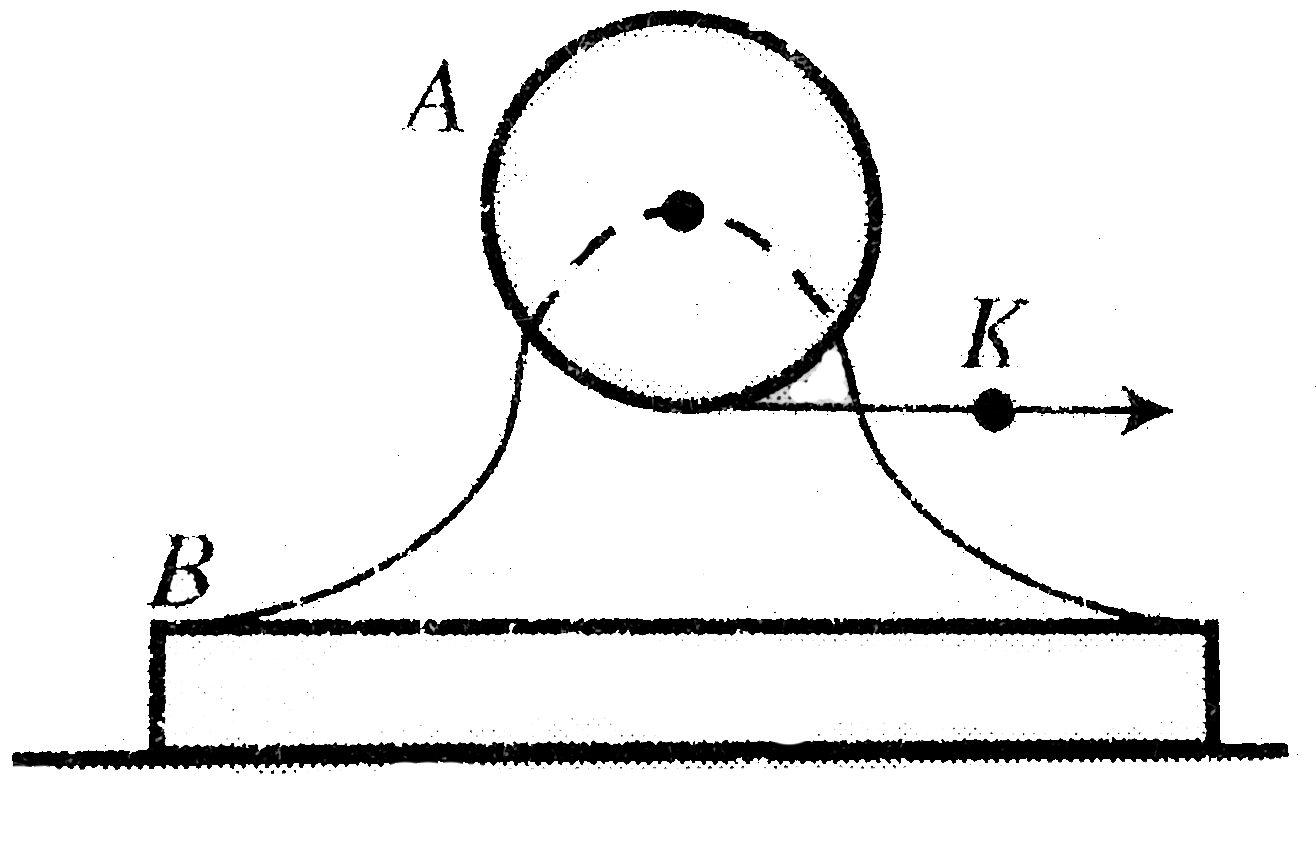
View SolutionTwo blocks A and B of equal mass m are connected through a massless string and arranged as shown in figure. The wedge is fixed on horizontal surface. Friction is absent everwhere. When the system is released from rest.
View SolutionTwo blocks A and B of equal mass m are connected through a massless string and arranged as shown in figure. The wedge is fixed on horizontal surface. Friction is absent everwhere. When the system is released from rest.

View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is
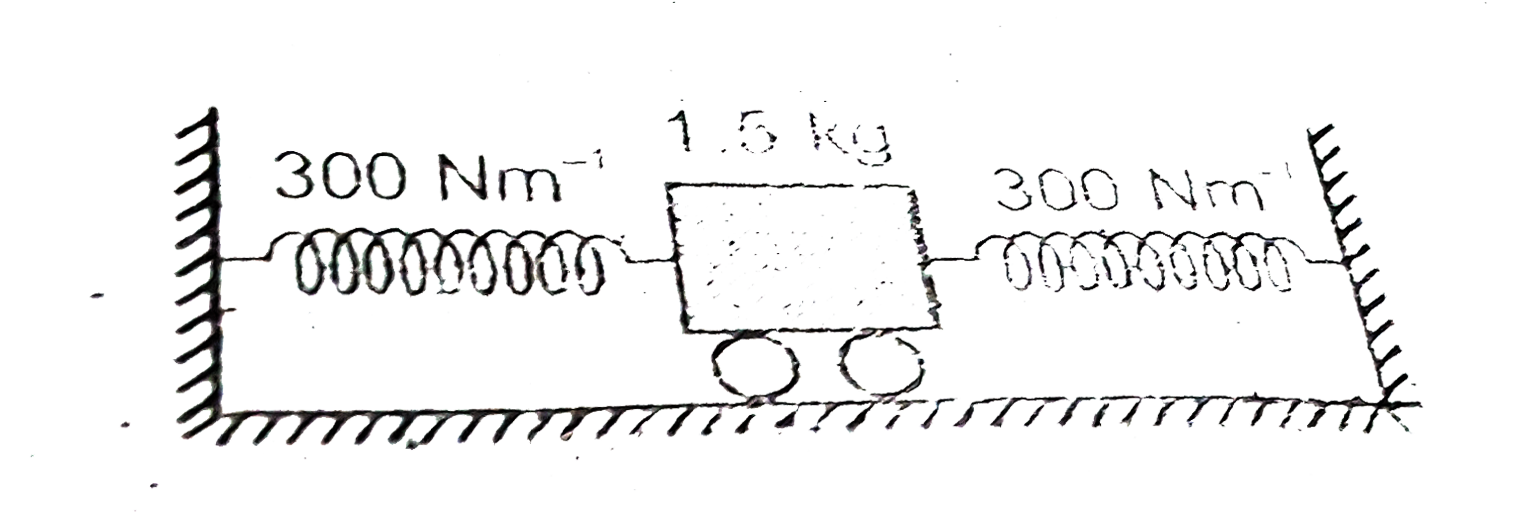
View SolutionA horizontal uniform rod of mass 'm' has its left end hinged to the fixed incline plane, while its right end rrests on the top of a uniform cylinder of mass 'm' which in turn is at rest on the fixed inclined plane as shown. The coefficient of friction between the cylinder and rod, and between the cylinder and inclined plane, is sufficient to keep the cylinder at rest.

The magnitude of normal reaction exerted by the rod on the cylinder is
View Solution
