A system consists three particles, each of mass M lying on the corners of an equilateral triangle of side 2l. If the length of each side of the triangle is decreased to l, without the gain in kinetic energy of the particles, the work done by an external agent is given by
−3GM22l
3GM22l
GM2l
−1.5GMl
To solve the problem, we need to calculate the work done by an external agent when the length of each side of the triangle formed by three particles is decreased from 2l to l. The work done can be determined by finding the change in potential energy of the system.
1. Identify the Initial Configuration:
- The three particles, each of mass M, are placed at the vertices of an equilateral triangle with side length 2l.
2. Calculate the Initial Potential Energy:
- The potential energy Uij between two particles of mass M separated by a distance r is given by:
Uij=−GM2r
- For our system, the initial potential energy Ui when the side length is 2l can be calculated as follows:
- Potential energy between the first and second particle:
U12=−GM22l
- Potential energy between the first and third particle:
U13=−GM22l
- Potential energy between the second and third particle:
U23=−GM22l
- Therefore, the total initial potential energy Ui is:
Ui=U12+U13+U23=−GM22l−GM22l−GM22l=−3GM22l
3. Identify the Final Configuration:
- The side length of the triangle is decreased to l.
4. Calculate the Final Potential Energy:
- Using the same formula for potential energy, we can calculate the final potential energy Uf when the side length is l:
- Potential energy between the first and second particle:
U12=−GM2l
- Potential energy between the first and third particle:
U13=−GM2l
- Potential energy between the second and third particle:
U23=−GM2l
- Therefore, the total final potential energy Uf is:
Uf=U12+U13+U23=−GM2l−GM2l−GM2l=−3GM2l
5. Calculate the Work Done by the External Agent:
- The work done W by the external agent is equal to the change in potential energy:
W=Uf−Ui
- Substituting the values we found:
W=(−3GM2l)−(−3GM22l)
- Simplifying this expression:
W=−3GM2l+3GM22l=−3GM2l+3GM22l=−6GM22l+3GM22l=−3GM22l
6. Final Result:
- The work done by the external agent is:
W=3GM22l
- The three particles, each of mass M, are placed at the vertices of an equilateral triangle with side length 2l.
- The potential energy Uij between two particles of mass M separated by a distance r is given by:
Uij=−GM2r
- For our system, the initial potential energy Ui when the side length is 2l can be calculated as follows:
- Potential energy between the first and second particle:
U12=−GM22l
- Potential energy between the first and third particle:
U13=−GM22l
- Potential energy between the second and third particle:
U23=−GM22l
- Therefore, the total initial potential energy Ui is:
Ui=U12+U13+U23=−GM22l−GM22l−GM22l=−3GM22l
- The side length of the triangle is decreased to l.
- Using the same formula for potential energy, we can calculate the final potential energy Uf when the side length is l:
- Potential energy between the first and second particle:
U12=−GM2l
- Potential energy between the first and third particle:
U13=−GM2l
- Potential energy between the second and third particle:
U23=−GM2l
- Therefore, the total final potential energy Uf is:
Uf=U12+U13+U23=−GM2l−GM2l−GM2l=−3GM2l
- The work done W by the external agent is equal to the change in potential energy:
W=Uf−Ui
- Substituting the values we found:
W=(−3GM2l)−(−3GM22l)
- Simplifying this expression:
W=−3GM2l+3GM22l=−3GM2l+3GM22l=−6GM22l+3GM22l=−3GM22l
- The work done by the external agent is:
W=3GM22l
Similar Questions
Three particle each of mass m are placed at the corners of equilateral triangle of side l

Which of the following is/are correct ?
View SolutionThree particles each of mass m are kept at vertices of an equilateral triangle of side L. The gravitational field at centre due to these particle is
View Solution
Knowledge Check
Three point masses each of mass m are placed at the corners of an equilateral triangle of side b. The moment of inertia of the system about an axis coinciding with one side of the triangle is
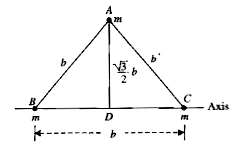 A3mb2Bmb2C(3/4)mb2D(2/3)mb2
A3mb2Bmb2C(3/4)mb2D(2/3)mb2Consider the charges q,q and -q placed at the vertices of an equilateral triangle of each side l. What is the force on each charge ?
Aq24√2πε0l2B−q24πε0l2Cq24πε0l2DzeroElectric charges q,q,–2q are placed at the corners of an equilateral triangle ABC of side l. The magnitude of electric dipole moment of the system is
AqlB√3qlCzeroD4ql
Three particles of equal mass 'm' are situated at the vertices of an equilateral triangle of side L. The work done in increasing the side of the triangle to 2L is
View SolutionThree masses 2 kg , 3kg and 4kg are lying at the corners of an equilateral triangle of side I. The X coordinate of center of mass is
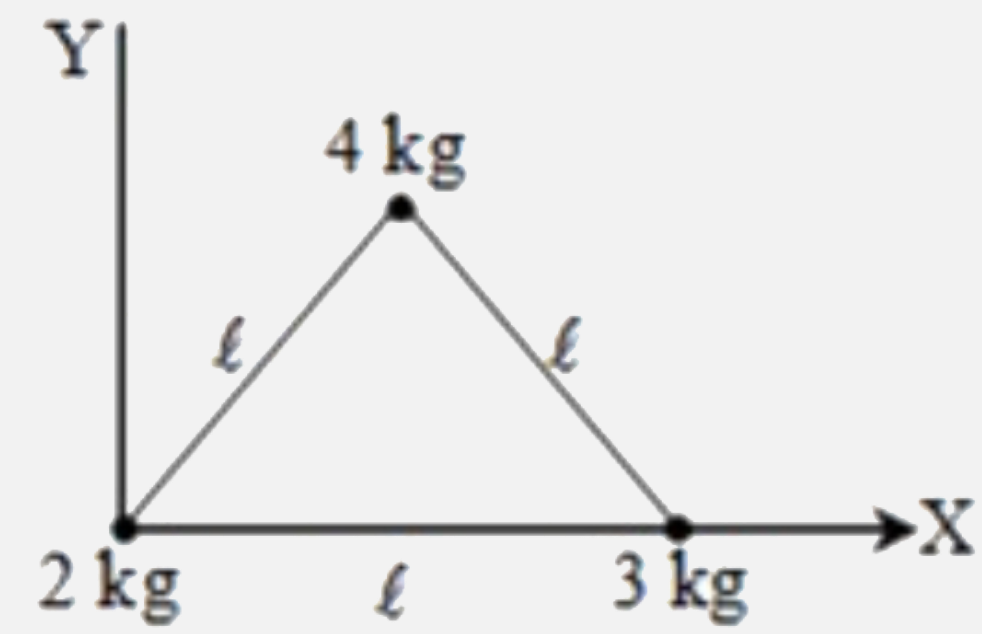
View SolutionThree particles A,B and C each of mass m are lying at the corners of an equilateral triangle of side L . If the particle A is released keeping the particles B and C fixed , the magnitude of instantaneous acceleration of A is
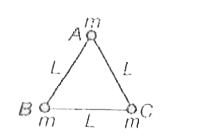
View SolutionThree identical rods, each of mass m and length l, form an equaliteral triangle. Moment of inertia about one of the sides is

View SolutionThree particles, each of mass 200 g are kept at the corners of an equilateral triangle of side 10 cm. Find the moment of inertia of the system about an axis
a. joining two of the particles
b. passing through one of the particle perpendicular to the plane of the particles.
View Solution
