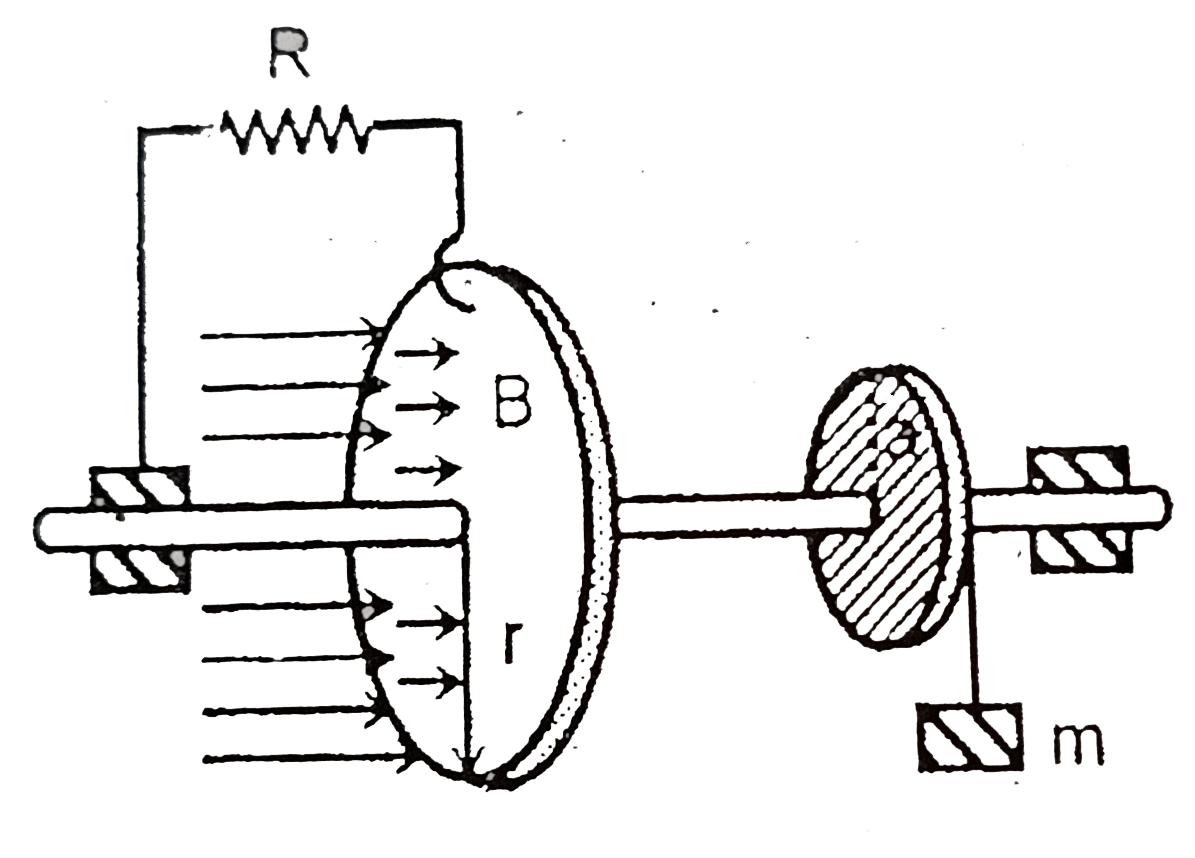
A metallic disc of radius r is made of a material of negligible resistance and can rotate about a conducting horizontal shaft. A smaller non conducting disc of radius a is fixed onto the same shaft and has a massless cord wrapped around it, which is attached to a small object of mass m as shown. Two ends of a resistor of resistance R are connected to the perimeter of the disc and to the shaft by sliding contacts. The system is then placed into a uniform horizontal magnetic field B and the mass m is released. Find the terminal angular velocity with which the disc will rotate finally.
(Take r=10cm, a=2cm, R=1100Ω, B=0.2T, m=50gm, g=10m/s2)
200rad/s
300rad/s
100rad/s
10rad/s
At terminal stage, torque applied on the smaller disc by the rope =mga
current to the disc =Bωr22R(where ω is terminal angular velocity)
torque applied by magnetic field =B2ωr44R
So, B2ωr44R=mga
ω=100rad/sec
Similar Questions
A semicircular metallic disc of radius R has two small cavities of radii r1and r2 as shown in the figure. On heating the disc

View SolutionA rod of length l and resistance r rotates about one end as shown in figure.Its othr end touches a conducting ring a of negligible resistance.A resistance R is connected between centre and periphery.Draw the electrical equivalence and find the current in the resistance R.There is a uniform magnetic field B directed as shown.

View SolutionA disc of radius r is removed from the centre of a disc of mass M and radius R. The M.I. About the axis through the centre and normal to the plane will be:
View SolutionA disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:

View SolutionA uniform disc of mass M and radius R is mounted on a fixed horizontal axis. A block of mass m hangs from a massless string that is wrapped around the rim of the disc. The magnitude of the acceleration of the falling block (m) is
View SolutionA uniform disc of mass M and radius R is mounted on an axle supported in frictionless bearings. A light cord is wrapped around the rim of the disc and a steady downward pull T is exerted on the cord. The angular acceleration of the disc is
View SolutionA circular metallic disc of radius R has a small circular cavity of radius r as shown in figure. On heating the system

View SolutionA rod of length L and resistance r rotates about one end as shown in . Its other end touches a conducting ring of negligible resistence. A resistence R is connected between the center and periphery. Draw the electrical equivalence and find the current in resistance R. There is a uniform magnetic field B directed as shown in .
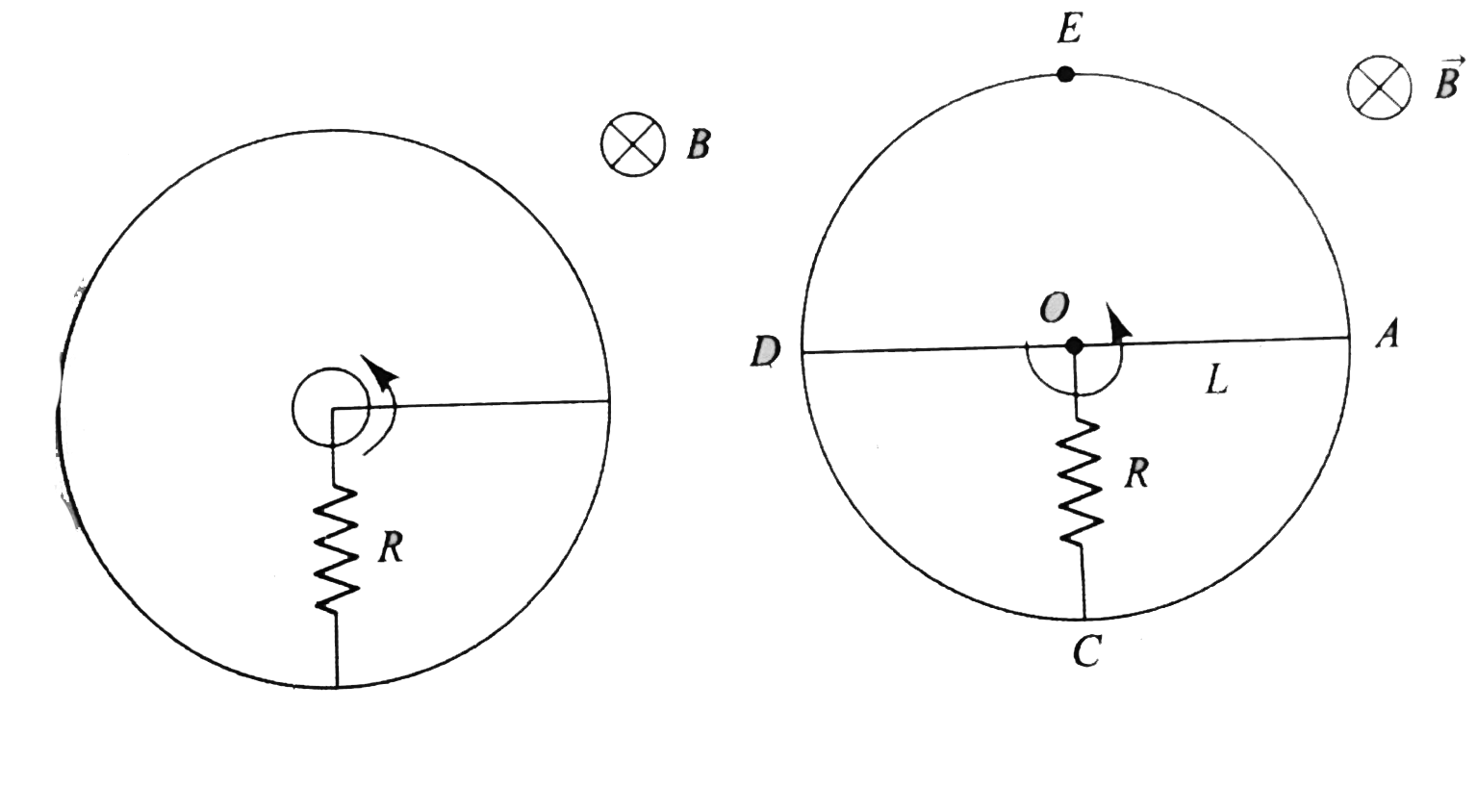
View SolutionA rod of length L and resistance r rotates about one end as shown in . Its other end touches a conducting ring of negligible resistence. A resistence R is connected between the center and periphery. Draw the electrical equivalence and find the current in resistance R. There is a uniform magnetic field B directed as shown in .

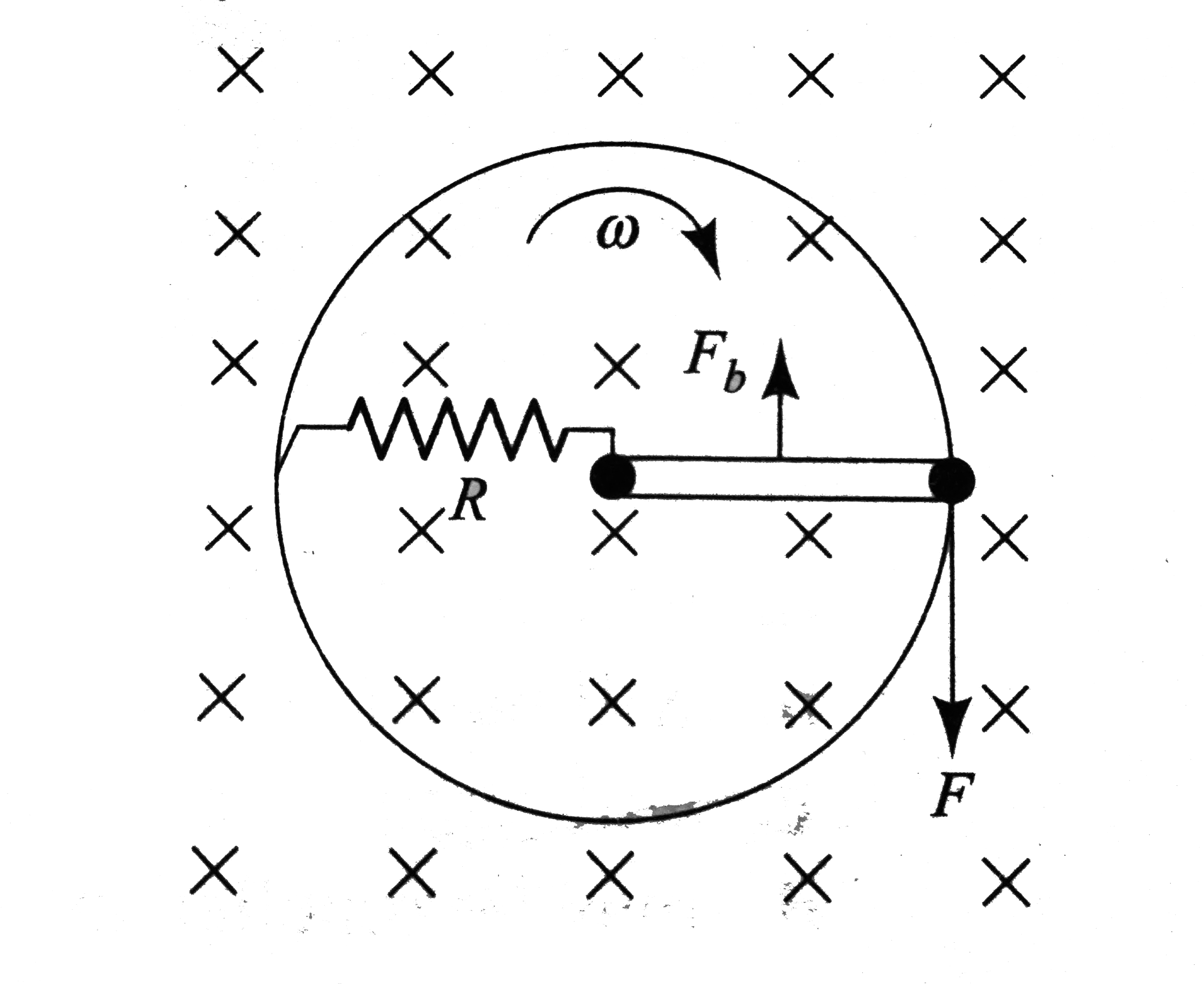
View SolutionA metallic ring of radius r with a uniform metallic spoke of negligible mass and length r is rotated about its axis with angular velocity ω in a perpendicular uniform magnetic field B as shown in Fig. 3.163. The central end of the spoke is connected to the rim of the wheel through a resistor R as shown. The resistor does not rotate, its one end is always at the center of the ring and the other end is always in as shown is needed to maintain constant angular velocity of the wheel. F is equal to (the ring and the spoke has zero resistance)
View Solution
