A capacitor initially given a charge Q0 is connected across a resistor R at t=0. The separation between the plates changes according to d=d0(1+t)(0≤t<1). A small bulb is connected across the plates of the capacitor which lights when potential difference across the plates of the capacitor reaches V0. Find
(a) the variation of charge with time
(b) time when the bulb will light.
To solve the problem step by step, we will analyze the behavior of the capacitor and the resistor, and derive the required expressions for charge variation and the time when the bulb lights up.
Step 1: Understand the relationship between charge, capacitance, and voltage.
The charge Q on a capacitor is related to the capacitance C and the voltage V across it by the equation:
Q=C⋅V
Step 2: Determine the capacitance as a function of time.
Given that the separation between the plates of the capacitor changes according to:
d(t)=d01+t
The capacitance C of a parallel plate capacitor is given by:
C=Aϵ0d
Substituting for d(t):
C(t)=Aϵ0d01+t=Aϵ0(1+t)d0
Step 3: Apply Kirchhoff's law to find the charge variation.
According to Kirchhoff's law, the voltage across the capacitor and the resistor must sum to zero:
QC+IR=0
Where I=−dQdt (the current is the negative rate of change of charge). Thus, we can write:
QC=−RdQdt
Substituting C(t):
QAϵ0(1+t)d0=−RdQdt
Rearranging gives:
dQQ=−Aϵ0d0Rdt1+t
Step 4: Integrate both sides.
Integrating from Q0 to Q on the left and from 0 to t on the right:
∫QQ0dQQ=−Aϵ0d0R∫t0dt1+t
This gives:
ln(QQ0)=−Aϵ0d0Rln(1+t)
Exponentiating both sides results in:
Q=Q0(1+t)−Aϵ0d0R
Step 5: Find the time when the bulb lights up.
The bulb lights up when the potential difference V across the capacitor reaches V0:
V=QC
Substituting for C(t):
V=QAϵ0(1+t)d0=Q⋅d0Aϵ0(1+t)
Setting V=V0:
V0=Q0(1+t)−Aϵ0d0R⋅d0Aϵ0(1+t)
Rearranging gives:
V0Aϵ0(1+t)=Q0d0(1+t)−Aϵ0d0R
Solving for t leads to:
t=(Q0d0V0Aϵ0)d0RAϵ0−1
Final Answers:
(a) The variation of charge with time is:
Q(t)=Q0(1+t)−Aϵ0d0R
(b) The time when the bulb will light is:
t=(Q0d0V0Aϵ0)d0RAϵ0−1
The charge Q on a capacitor is related to the capacitance C and the voltage V across it by the equation:
Q=C⋅V
Given that the separation between the plates of the capacitor changes according to:
d(t)=d01+t
The capacitance C of a parallel plate capacitor is given by:
C=Aϵ0d
Substituting for d(t):
C(t)=Aϵ0d01+t=Aϵ0(1+t)d0
According to Kirchhoff's law, the voltage across the capacitor and the resistor must sum to zero:
QC+IR=0
Where I=−dQdt (the current is the negative rate of change of charge). Thus, we can write:
QC=−RdQdt
Substituting C(t):
QAϵ0(1+t)d0=−RdQdt
Rearranging gives:
dQQ=−Aϵ0d0Rdt1+t
Integrating from Q0 to Q on the left and from 0 to t on the right:
∫QQ0dQQ=−Aϵ0d0R∫t0dt1+t
This gives:
ln(QQ0)=−Aϵ0d0Rln(1+t)
Exponentiating both sides results in:
Q=Q0(1+t)−Aϵ0d0R
The bulb lights up when the potential difference V across the capacitor reaches V0:
V=QC
Substituting for C(t):
V=QAϵ0(1+t)d0=Q⋅d0Aϵ0(1+t)
Setting V=V0:
V0=Q0(1+t)−Aϵ0d0R⋅d0Aϵ0(1+t)
Rearranging gives:
V0Aϵ0(1+t)=Q0d0(1+t)−Aϵ0d0R
Solving for t leads to:
t=(Q0d0V0Aϵ0)d0RAϵ0−1
(a) The variation of charge with time is:
Q(t)=Q0(1+t)−Aϵ0d0R
t=(Q0d0V0Aϵ0)d0RAϵ0−1
Similar Questions
A capacitor given a charge Q0 is conected across a resistor R at t = 0. The separation between the plates changes according to d=d(1+t)(0≤t<1) Find the variation of charge on capacitor with time.

View SolutionIf A is connerted with D and B is connected with C find the potential difference a across each capacitor and the final charge in each capacitor.
View Solution
Knowledge Check
A capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
AC1VC1+C2BC2VC1+C2C1+C2C1D1−C2C1
A capacitor is charged to a potential difference of 100 V and is then connected across a resistor. The potential difference across the capacitor decays exponentially with respect to time. After 1 sec, the P.D. between the plates of the capacitor is 80 V. what will be the potential difference between the plates after 2 sec ?
View SolutionIn the circuit in Fig. switch S1 was closed for a long time . At time t=0 the switch is opened.
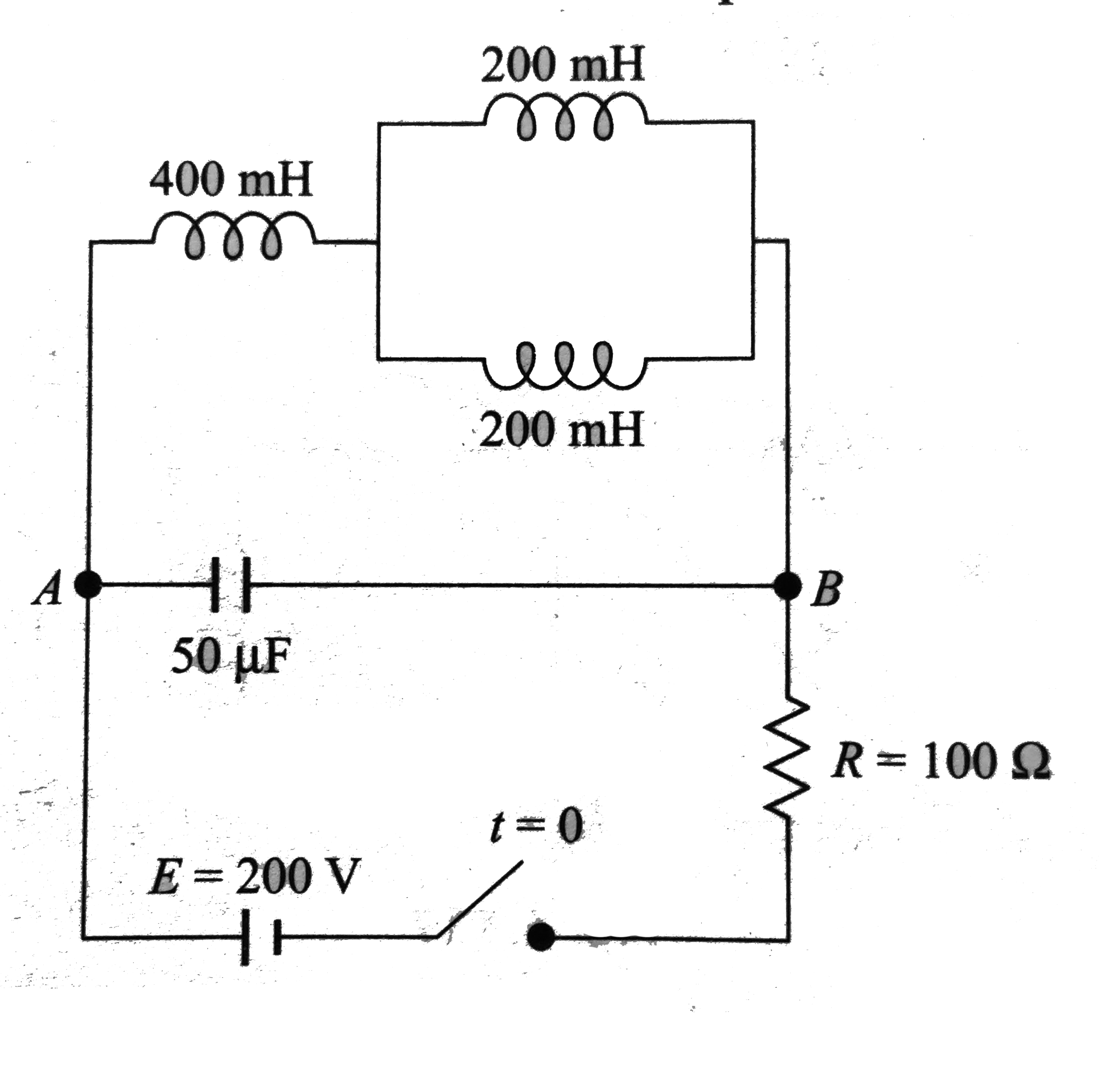
Find the maximum potentail difference across the plates of the capacitor after the switch is opened.
View SolutionIn the circuit shown in fig, switch S was closed for long time. At time t-0, the switch is opened again. The maximum potential difference across the plates of the capacitor after the switch is opened is

View SolutionA capacitor is connected to a variable source of potential. Current flowing in the circuit and potential across the plates of capacitor at time t are shown in figure.

Capacity of the capacitor is
View SolutionA 10V battery is connected to two capacitors C1 and C2 and a resistor R. When the capacitors are fully charged, then the potential difference across the resistor will be
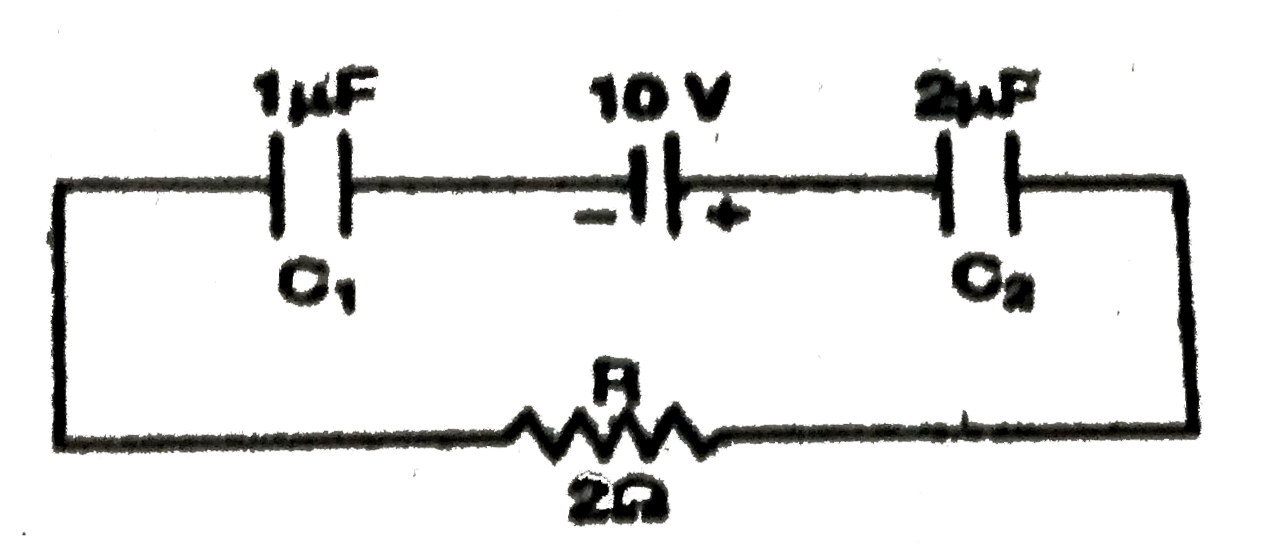
View SolutionFind potential difference across the plates AB if capacitance between the plates is C and area of each plate is equal and Q1,Q2(<Q1) are charges given to the plates
View SolutionThe charging current for a capacitor is 0.25A. What is the displacement current across its plates?
View Solution

