A small ball is rolled with speed u from piont A along a smooth circular track as shown in figure. If x=3R, then

Determine the required speed u so that the ball returns to A, the point of projection after passing through C, the highest point.
We determine the velocity at C so that it reaches A along a parbolic trajectory, then applying the law of conservation of energy to the motion ABC (as non-conservative force are absent)
v= velocity at point C=32√gR
applying conservation of energy from A to C
12μ2=2mgR+12mv2
⇒u=52√gR
Similar Questions
A small ball is rolled with speed u from piont A along a smooth circular track as shown in figure. If x=3R, then

What is the minimum value of x for which the ball can reach the point of projection after reaching C?
View SolutionA small spherical ball is released from a point at a height h on a rough track shown in figure. Assuming that it does not slip anywhere, find its linear speed when it rolls on the horizontal part of the track.

View SolutionA ball of mass m is released from A inside a smooth wedge of mass m as shown in figure. What is the speed of the wedge when the ball reaches point B?
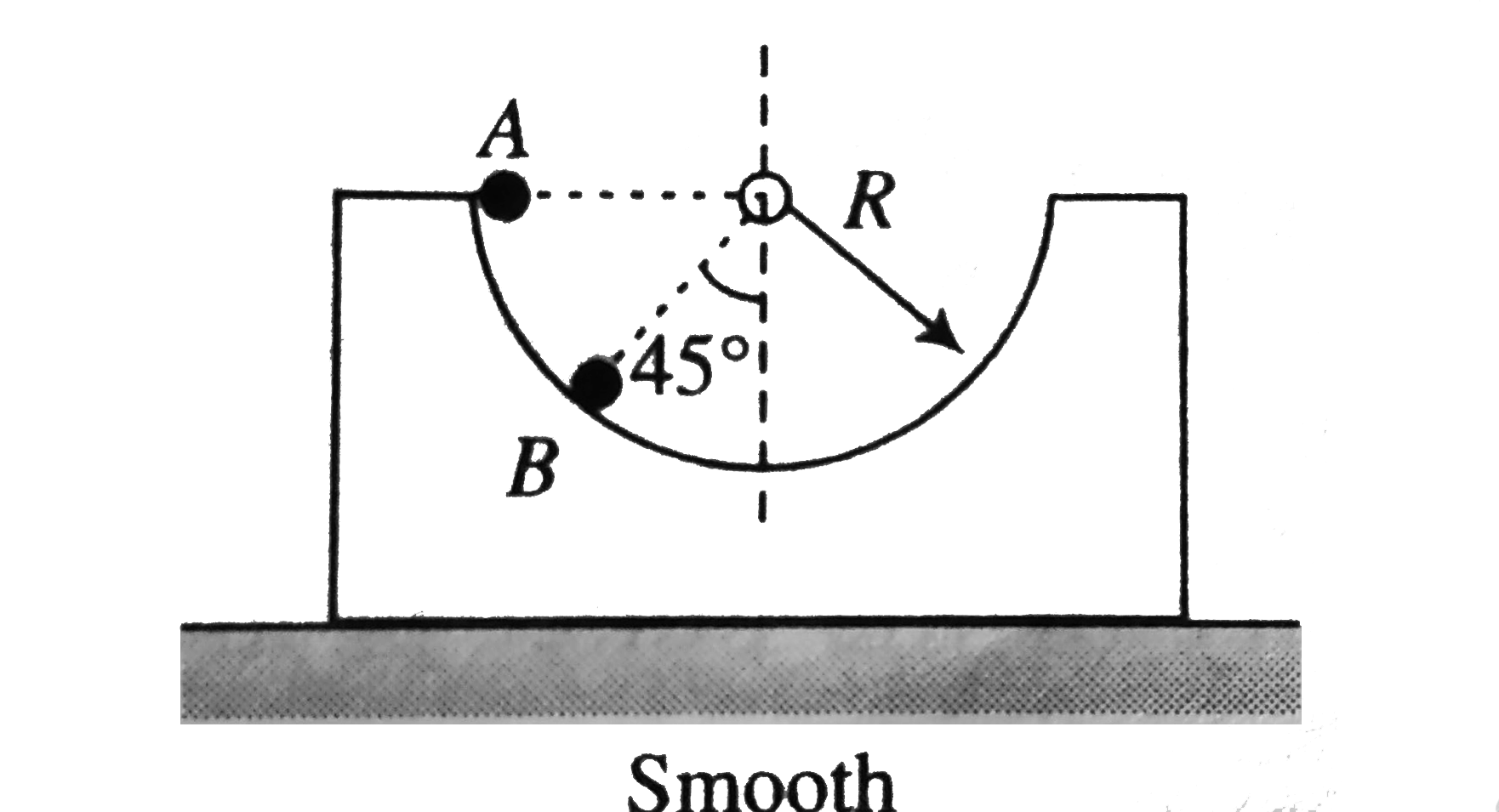
View SolutionA smooth circular table is surrounded by a rim whose interior is vertical . A ball is projected along the table from a point on the rim in a direction making an angle θ to the radius through the point and returns to the point of projection after two impacts . If e be the coefficient of restitution, then
View SolutionA particle of mass m is projected with speed √Rg4 from top of a smooth hemisphere as shown in figure. If the particle starts slipping from the highest point, then the horizontal distance between the point where it leaves contact with sphere and the point at which the body was placed is
View SolutionA small ball is pushed from a height h along a smooth hemispherical bowl of radius R. With what speed should the ball be pushed so that it just reaches the top of the opposite end of the bowl?
View SolutionA cylindrical hall has a horizontal smooth floor. A ball is projected along the floor from A point on the wall in a direction making an angle θ with the radius through the point the ball returns bak to the initial point after two impacts with the wall. if the coefficient of restitution is e than tan2θ will be
View SolutionA small ball is projected from point P towards a vertical wall as shown in Fig. It hits the wall when its velocity is horizontal. Ball reaches point P after one bounce on the floor. The coefficient of restitution assuming it to be same for two collisions is n/2. All surfaces are smooth. Find the value of n.

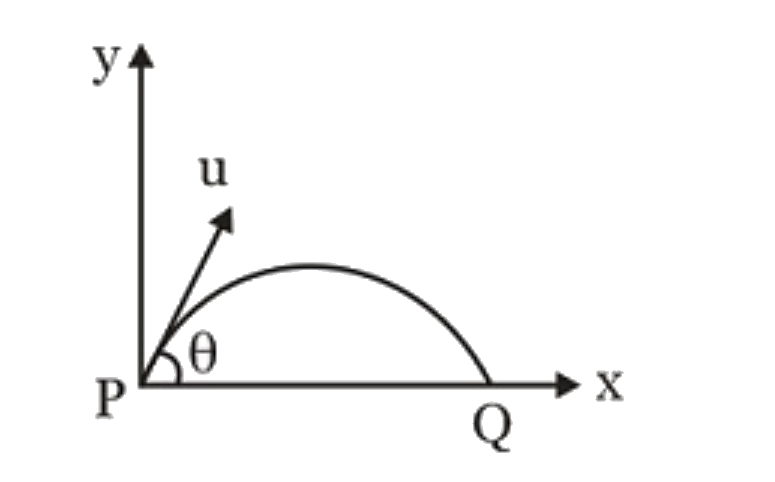
View SolutionA particle of mass m , initial speed u and angle of projection θ is projected as shown in the figure. Average torque on the projectile between initial and final positions P and Q about the point of projection is
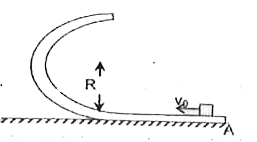
View SolutionA small block is projected with a speed v0 on a horizontal track placed on a sufficiently rough surface which turns into a semi circle ( vertical) of radius R. Find the min value of Vo so that the body will hit the point A after leaving the track at its highest point. The arrangement is shown in the figure, given that the straight part is rough & the curved path is smooth. The coefficient of friction is μ.
View Solution
