Two sound waves of frequencies 100Hz and 102Hz and having same amplitude 'A' are interfering. At a stationary detector, which can detect resultant amplitude greater than or equal to A. So, in a given time interval of 12 seconds, finds the total duration in which detector is active.
The correct Answer is:8
To solve the problem, we need to determine the total duration in which the detector is active when two sound waves of frequencies 100 Hz and 102 Hz interfere with each other. The detector is active when the resultant amplitude is greater than or equal to the amplitude A.
1. Determine the Beat Frequency:
The beat frequency fb is given by the difference in frequencies of the two sound waves:
fb=|f2−f1|=|102Hz−100Hz|=2Hz
2. Calculate the Time Period of Beats:
The time period Tb of the beats is the inverse of the beat frequency:
Tb=1fb=12Hz=0.5seconds
3. Determine the Duration of Active Time in One Beat Cycle:
In one cycle of beats (0.5 seconds), the amplitude will be equal to or greater than A for a certain duration. The amplitude reaches its maximum when the cosine term in the interference equation is equal to 1, and it is zero when the cosine term is equal to -1.
The condition for the resultant amplitude R to be at least A can be expressed as:
R=2Acos(2πTbt)≥A
This simplifies to:
cos(2πTbt)≥12
4. Find the Angles for the Condition:
The cosine function is equal to 12 at angles π3 and 5π3. Therefore, we can find the time intervals:
2πTbt=π3⇒t=Tb6=0.56=112seconds
2πTbt=5π3⇒t=5Tb6=5×0.56=512seconds
5. Calculate the Duration of Active Time:
The duration during which the amplitude is at least A in one cycle is:
Active Time=tmax−tmin=(512−112)=412=13seconds
6. Determine the Number of Cycles in 12 Seconds:
The number of cycles in 12 seconds is:
Number of cycles=12Tb=120.5=24
7. Calculate Total Active Time in 12 Seconds:
The total active time in 12 seconds is:
Total Active Time=Number of cycles×Active Time per cycle=24×13=8seconds
Final Answer:
The total duration in which the detector is active in 12 seconds is 8 seconds.
The beat frequency fb is given by the difference in frequencies of the two sound waves:
fb=|f2−f1|=|102Hz−100Hz|=2Hz
The time period Tb of the beats is the inverse of the beat frequency:
Tb=1fb=12Hz=0.5seconds
In one cycle of beats (0.5 seconds), the amplitude will be equal to or greater than A for a certain duration. The amplitude reaches its maximum when the cosine term in the interference equation is equal to 1, and it is zero when the cosine term is equal to -1.
R=2Acos(2πTbt)≥A
This simplifies to:
cos(2πTbt)≥12
The cosine function is equal to 12 at angles π3 and 5π3. Therefore, we can find the time intervals:
2πTbt=π3⇒t=Tb6=0.56=112seconds
2πTbt=5π3⇒t=5Tb6=5×0.56=512seconds
The duration during which the amplitude is at least A in one cycle is:
Active Time=tmax−tmin=(512−112)=412=13seconds
The number of cycles in 12 seconds is:
Number of cycles=12Tb=120.5=24
The total active time in 12 seconds is:
Total Active Time=Number of cycles×Active Time per cycle=24×13=8seconds
The total duration in which the detector is active in 12 seconds is 8 seconds.
Similar Questions
Two sound waves travelling in the same direction are superposed. Their frequencies are 300and302Hz and their amplitudes are 0.2and0.3mm, respectively
a. What is the number of beats per second ?
b. What are the maximum and minimum values of resultant amplitude during the formation of beats ?
c. Calculate the ratio of maximum and minimum intensities of the resultant sound.
View SolutionThe planes sources of sound of frequency n1=400Hz,n2=401Hz of equal amplitude of a each, are sounded together. A detector receives waves from the two sources simultaneously. It can detect signals of amplitude with magnitude ≥ a only,
View SolutionA soure of sound of frequency 165 hz is placed in front of a wall at a distance 2 m from it. A dtector is also placed in front of the wall at the same distance from it. Find the minimum distance between the source and detector for which maximum sound is recorded int he detector . the speed of sound is 330 m/s
View SolutionA whistle of frequency f0 = 1300 Hz is dropped from a height H = 505 m above the ground. At the same time, a detector is projected upwards with velocity v=50ms−1 along the same line. If the velocity of sound is c=300ms−1 find the frequency detected by the detector after t = 5s.
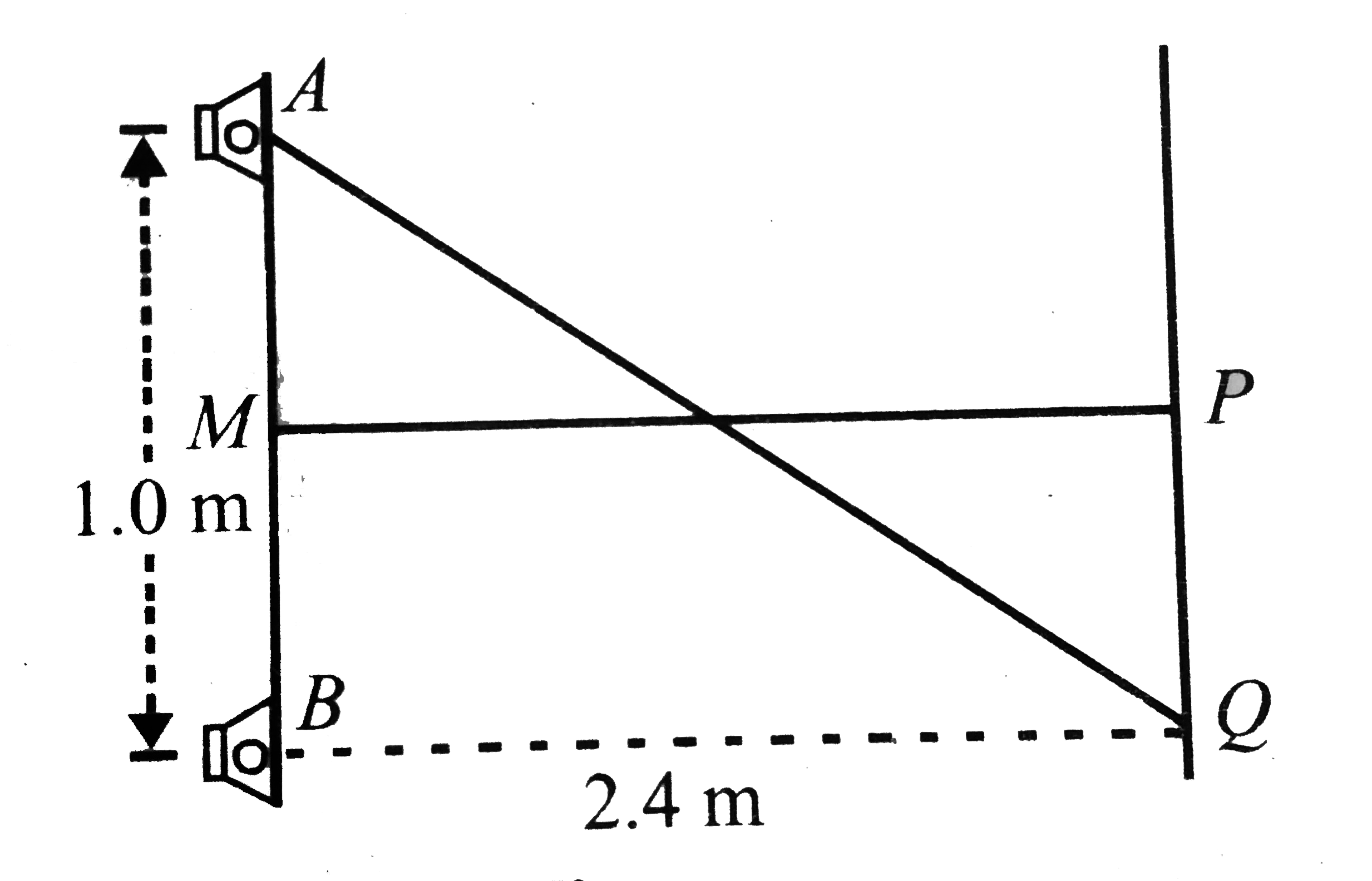
View SolutionTwo small loudspeakers A,B ( 1m apart) are connected to the same oscillator so that both emit sound waves of frequency 1700Hz in phase . A sensitive detector , detects a maximum wave at P on the perpendicular bisector MPofAB and another maximum wave when it first reaches a point Q directly opposite to B. Calculate the speed c of the sound waves in air .
View SolutionTwo waves, each having a frequency of 100 Hz and a wavelength of 2.0 cm, are travelling in the same direction on a string. What is the phase difference between the waves if the second wave was produced 0.015 s later than the first one at the same place,
View SolutionA source of sound is moving along a circular orbit of radius 3meter with an angular velocity of 10rad/s. A sound detector located far away from the source is executing linear simple harmonic motion along the line BD with an amplitude BC=CD=6meters. The frequency of oscillation of the detector is 5π per second. The source is at the point A when the detector is at the point B. If the source emits a continuous sound wave of frequency 340Hz, Find the maximum and the minimum frequencies recorded by the detector.

View SolutionA diode detector is used to detect and amplitude modulated wave of 60% modulation by using a condenser of capacity 250 pF in parallel with a load resistance 100kΩ. Find the maximum modulated frequency which could be detected by it
View SolutionTwo waves, each having a frequency of 100 Hz and a wavelength of 2.0 cm, are travelling in the same direction on a string. What is the phase difference between the waves (a) if the second wave was produced 0.015 s later than the first one at the same place, (b) if the two waves were produced at the same instant but the first one was produced a distance 4.0 cm behind the second one ? (c) If each of the waves has an amplitude of 2.0 mm, what would be the amplitudes of the resultant waves in part (a) and (b) ?
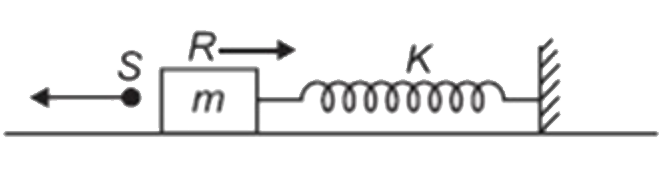
View SolutionA sound source S, emitting a sound of frequency 400 Hz and a receiver R of mass m are at the same point. R is performing SHM with the help of a spring of force constant K. At a time t = 0, R is at the mean position and moving towards the right, as shown. At the same time, the source starts moving away from R with some acceleration a. The frequency registered by the receiver at a time t = 10 s is 250 Hz. What is the time (in seconds) at which the corresponding registered frequency of 250 Hz was emitted by the source? [Given that mK=25π2 and amplitude of oscillation = 100πm,Vsound = 320 m s^(-1)]
View Solution
