Suppose 50 bacterial are placed in a flask containing nutrients
for the bacteria so that they can multiply. A study at 35∘C gave the following results:
Time: (minutes) 0,15,30,45,60
Number of bacteria 100,,200,400,800,1600
The t1/2 for the reaction is,
1.5 sec
1.5 min
150 min
15 min
The correct Answer is:D
To solve the problem of determining the half-life (t₁/₂) for the bacterial growth in the flask, we can follow these steps:
1. Understanding the Growth Pattern:
- We start with 50 bacteria, and the number of bacteria doubles every 15 minutes. The given data shows:
- At 0 minutes: 100 bacteria
- At 15 minutes: 200 bacteria
- At 30 minutes: 400 bacteria
- At 45 minutes: 800 bacteria
- At 60 minutes: 1600 bacteria
2. Identifying the Doubling Time:
- The time taken for the bacteria to double in number is 15 minutes. This is crucial for calculating the half-life.
3. Relating Doubling Time to Half-Life:
- For a first-order reaction, the relationship between the doubling time (t_d) and half-life (t₁/₂) can be expressed as:
td=t1/2⋅ln(2)
- Since we know that the doubling time is 15 minutes, we can rearrange this formula to find the half-life:
t1/2=tdln(2)
4. Calculating Half-Life:
- The natural logarithm of 2 (ln(2)) is approximately 0.693. Thus, we can substitute the values:
t1/2=15 minutes0.693≈21.65 minutes
5. Conclusion:
- The half-life for the reaction, based on the doubling time of the bacteria, is approximately 21.65 minutes.
Final Answer:
The half-life (t₁/₂) for the reaction is approximately 21.65 minutes.
---
- We start with 50 bacteria, and the number of bacteria doubles every 15 minutes. The given data shows:
- At 0 minutes: 100 bacteria
- At 15 minutes: 200 bacteria
- At 30 minutes: 400 bacteria
- At 45 minutes: 800 bacteria
- At 60 minutes: 1600 bacteria
- The time taken for the bacteria to double in number is 15 minutes. This is crucial for calculating the half-life.
- For a first-order reaction, the relationship between the doubling time (t_d) and half-life (t₁/₂) can be expressed as:
td=t1/2⋅ln(2)
- Since we know that the doubling time is 15 minutes, we can rearrange this formula to find the half-life:
t1/2=tdln(2)
- The natural logarithm of 2 (ln(2)) is approximately 0.693. Thus, we can substitute the values:
t1/2=15 minutes0.693≈21.65 minutes
- The half-life for the reaction, based on the doubling time of the bacteria, is approximately 21.65 minutes.
The half-life (t₁/₂) for the reaction is approximately 21.65 minutes.
Similar Questions
Suppose 50 bacterial are placed in a flask containing nutrients
for the bacteria so that they can multiply. A study at 35∘C gave the following results:
Time: (minutes) 0,15,30,45,60
Number of bacteria 100,,200,400,800,1600
The rate of reaction initially is:
View SolutionA diet to two foods F1andF2 contains nutrients thiamine, phosphorous and iron. The amount of each nutrient in each of the food (in milligrams per 25 gms) is given in the following table: Food Nutrients, F1 , F2 Thiamine, 0.25, 0.10 Phosphorous, 0.75, 1.50 Iron, 1.60, 0.80 The minimum requirement of the nutrients in the diet are 1.00 mg of thiamine, 7.50mg of phosphorous and 10.00 mg of iron. The cost F1 is 20 paise per 25 gms while the cost of F2 is 15 paise per 25 gms. Find the minimum cost of diet.
View SolutionA biologist places a colony consisting of 5000 bacteria into a petri dish. After the intial placement of the bacteria at time t = 0, the biologist measures and estimates the number of bacteria present every half hour. This data was then fitted by an exponential curve of the form y=c.2kt where c and k are constants, t is measured in hours, and y is measured in thousands of bacteria. The scatterplot together with the exponential curve are shown below.
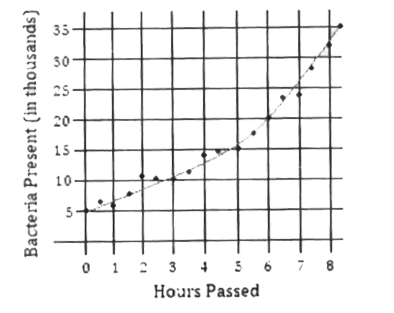
Suppose that the data was fitted with a quadratic function of the form t2+bt+c instead of an exponential function. Assume that the quadratic funtion agrees with the scatterplot at times t = 0 and t = 6. What is the t - coordinate of the vertex of the graph of the quadratic function?
View SolutionThe index of refraction of a glass plate is 1.48 at θ1=30.∘C and varies linearly with temperature with a coefficient of 2.5×10−5.∘C−1. The coefficient of linear expansion of the glass is 5×10−9^∘C−1. At 30.∘C, the length of the glass plate is 3 cm. This plate is placed in front of one of the slit n Young's double-slit experiment. If the plate is being heated so that it temperature increases at a rate of 5∘C−1 min, the light sources has wavelength λ=589nm and the glass plate initially ia at θ=30∘C. The number of fringes that shift on the screen in each minute is nearly (use approximation)
View SolutionAn insurance company selected 2000 drivers at random in a particular city to find a relationship between age and accidents. The obtained are given in the following table: Age of Drivers (in years) Accidents in one year 0 1 2 3 over 3 18-29 30-50 above 50 440 505 360 160 125 45 110 60 35 61 22 15 35 18 9 Find the probability of the following events for a driver chosen at random from the life city: i) being 18-29 years of age and having exactly 3 accidents in one year. ii) being 30-50 years of age and having one or more accidents in a year. iii) having no accidents in one year.
View SolutionFollowing are two first order reaction with their half times given at 25∘C.
At1/2=30min−−−−−−−→ Products
Bt1/2=40min−−−−−−−→ Products
The temperature coefficients of their reactions rates are 3 and 2, respectively, beween 25∘C and 35∘C. IF the above two resctions are carried out taking 0.4M of each reactant but at different temperatures: 25∘C for the first order reaction and 35∘C for the second order reaction, find the ratio of the concentrations of A and B after an hour.
View SolutionScientists are working hard to develop nuclear fusion reactor Nuclei of heavy hydrogen, _(1)2H , known as deuteron and denoted by D, can be thought of as a candidate for fusion rector . The D−D reaction is _(1)2H+21H→12He+n+ energy. In the core of fusion reactor, a gas of heavy hydrogen of _(1)2H is fully ionized into deuteron nuclei and electrons. This collection of _12H nuclei and electrons is known as plasma . The nuclei move randomly in the reactor core and occasionally come close enough for nuclear fusion to take place. Usually , the temperature in the reactor core are too high and no material will can be used to confine the to plasma for a time t0 before the particles fly away from the core. If n is the density (number volume ) of deuterons , the productnt0is called Lawson number. In one of the criteria , a reactor is termed successful if Lawson number is greater then 5×1014s/cm2
it may be helpfull to use the following boltzmann constant
λ=8.6×10−5eV/k,e24πs0=1.44×10−9eVm
Result of calculations for four different design of a fusion reactor using D−D reaction are given below. which of these is most promising based on Lawson criterion ?
View SolutionScientists are working hard to develop nuclear fusion reactor Nuclei of heavy hydrogen, _(1)2H , known as deuteron and denoted by D, can be thought of as a candidate for fusion rector . The D−D reaction is _(1)2H+21H→12He+n+ energy. In the core of fusion reactor, a gas of heavy hydrogen of _(1)2H is fully ionized into deuteron nuclei and electrons. This collection of _12H nuclei and electrons is known as plasma . The nuclei move randomly in the reactor core and occasionally come close enough for nuclear fusion to take place. Usually , the temperature in the reactor core are too high and no material will can be used to confine the to plasma for a time t0 before the particles fly away from the core. If n is the density (number volume ) of deuterons , the productnt0is called Lawson number. In one of the criteria , a reactor is termed successful if Lawson number is greater then 5×1014s/cm2
it may be helpfull to use the following boltzmann constant
λ=8.6×10−5eV/k,e24πs0=1.44×10−9eVm
In the core of nucleus fusion reactor , the gas become plasma because of
View SolutionScientists are working hard to develop nuclear fusion reactor Nuclei of heavy hydrogen, _(1)2H , known as deuteron and denoted by D, can be thought of as a candidate for fusion rector . The D−D reaction is _(1)2H+21H→12He+n+ energy. In the core of fusion reactor, a gas of heavy hydrogen of _(1)2H is fully ionized into deuteron nuclei and electrons. This collection of _12H nuclei and electrons is known as plasma . The nuclei move randomly in the reactor core and occasionally come close enough for nuclear fusion to take place. Usually , the temperature in the reactor core are too high and no material will can be used to confine the to plasma for a time t0 before the particles fly away from the core. If n is the density (number volume ) of deuterons , the productnt0is called Lawson number. In one of the criteria , a reactor is termed successful if Lawson number is greater then 5×1014s/cm2
it may be helpfull to use the following boltzmann constant
λ=8.6×10−5eV/k,e24πs0=1.44×10−9eVm
In the core of nucleus fusion reactor , the gas become plasma because of
View SolutionWater is drained from a vertical cylindrical tank by opening a valve at the base of the tank. It is known that the rate at which the water level drops is proportional to the square root of water depth y, where the constant of proportionality k>0 depends on the acceleration due to gravity and the geometry of the hole. If t is measured in minutes and k=115, then the time to drain the tank if the water is 4 m deep to start with is (a) 30 min (b) 45 min (c) 60 min (d) 80 min
View Solution
