A uniformly charged square plate having side L carries a uniform surface charge density σ. The plate lies in the y−z plane with its centre at the origin. A point charge q lies on the x-axis. The flux of the electric field of q through the plate is ϕ0, while the foce on the point charge q due to the plate is F0, along the x-axis. Then,
σ=F0ϕ0L
σ=F0ϕ0
σ=F0Lϕ0
σ=ϕ0F0
The correct Answer is:B
To solve the problem, we need to analyze the relationship between the electric flux through the square plate and the force on the point charge due to the plate.
1. Understanding the Setup:
- We have a uniformly charged square plate with side length L lying in the y−z plane, centered at the origin.
- The surface charge density of the plate is σ.
- A point charge q is located on the x-axis.
2. Electric Flux (Φ0):
- The electric flux Φ0 through the plate due to the point charge q can be expressed using Gauss's law:
Φ0=qϵ0
- Here, ϵ0 is the permittivity of free space.
3. Force (F0) on the Point Charge:
- The force F0 on the point charge q due to the electric field E created by the charged plate can be calculated using:
F0=qE
- The electric field E due to a uniformly charged infinite plane sheet is given by:
E=σ2ϵ0
- However, since we have a square plate, we need to consider the effective area and the distance from the charge to the plate.
4. Relating F0 and Φ0:
- We can write F0 in terms of Φ0:
F0=q(σ2ϵ0)
- Substituting Φ0 into the equation gives:
F0=q(σ2ϵ0)
5. Dimensional Analysis:
- The dimensions of σ (surface charge density) can be expressed as:
\sigma = \frac{Q}{L^2} \quad \text{(where Q is charge)}
- The dimensions of force F0 are (MLT−2) and the dimensions of electric flux Φ0 are (E)(A)=(ML3T−3).
- From the above relationships, we can derive that:
σ=F0Φ0
6. Conclusion:
- The relationship between the surface charge density σ, the electric flux Φ0, and the force F0 is:
σ=F0Φ0
Final Answer:
The correct statement for the surface charge density σ is:
σ=F0Φ0
- We have a uniformly charged square plate with side length L lying in the y−z plane, centered at the origin.
- The surface charge density of the plate is σ.
- A point charge q is located on the x-axis.
- The electric flux Φ0 through the plate due to the point charge q can be expressed using Gauss's law:
Φ0=qϵ0
- Here, ϵ0 is the permittivity of free space.
- The force F0 on the point charge q due to the electric field E created by the charged plate can be calculated using:
F0=qE
- The electric field E due to a uniformly charged infinite plane sheet is given by:
E=σ2ϵ0
- However, since we have a square plate, we need to consider the effective area and the distance from the charge to the plate.
- We can write F0 in terms of Φ0:
F0=q(σ2ϵ0)
- Substituting Φ0 into the equation gives:
F0=q(σ2ϵ0)
- The dimensions of σ (surface charge density) can be expressed as:
\sigma = \frac{Q}{L^2} \quad \text{(where Q is charge)}
- The dimensions of force F0 are (MLT−2) and the dimensions of electric flux Φ0 are (E)(A)=(ML3T−3).
- From the above relationships, we can derive that:
σ=F0Φ0
- The relationship between the surface charge density σ, the electric flux Φ0, and the force F0 is:
σ=F0Φ0
The correct statement for the surface charge density σ is:
σ=F0Φ0
Similar Questions
A positively charged ring is in y - z plane with its centre at origin . A positive test charge qe , held at origin is released along x axis, then its speed
View SolutionA charge q is placed st the centre of a spher. Taking outward normal as positive, find the flux of the electric field through the surface of the sphere due to the enclosed charge.
View SolutionA point charge 'q' is placed at a distance l' (on th y-axis) vertically above the surface which lies in the xz plane as shown in the figure. The flux of electric field passing through the plate is

View SolutionTwo point charges (Q each are placed at (0,y) and (0-y) A point charge q of the same polarity can move along the x-axis. Then
View SolutionA point charge placed on the axis of a uniformly charged disc experiences a force f due to the disc. If the charge density on the disc σ is, the electric flux through the disc, due to the point charge will be
View SolutionA charge 'Q' is placed at the centre of a hemispherical surface of radius 'R'. The flux of electric field due to charge 'Q' through the surface of hemisphere is
View SolutionA square of side d, made from a thin insulating plate, is uniformly charged and carries a total charge of Q. A point charge q is placed on the symmetrical normal axis of the square at a distance d/2 from the plate. How large is the force acting on the point charge ?
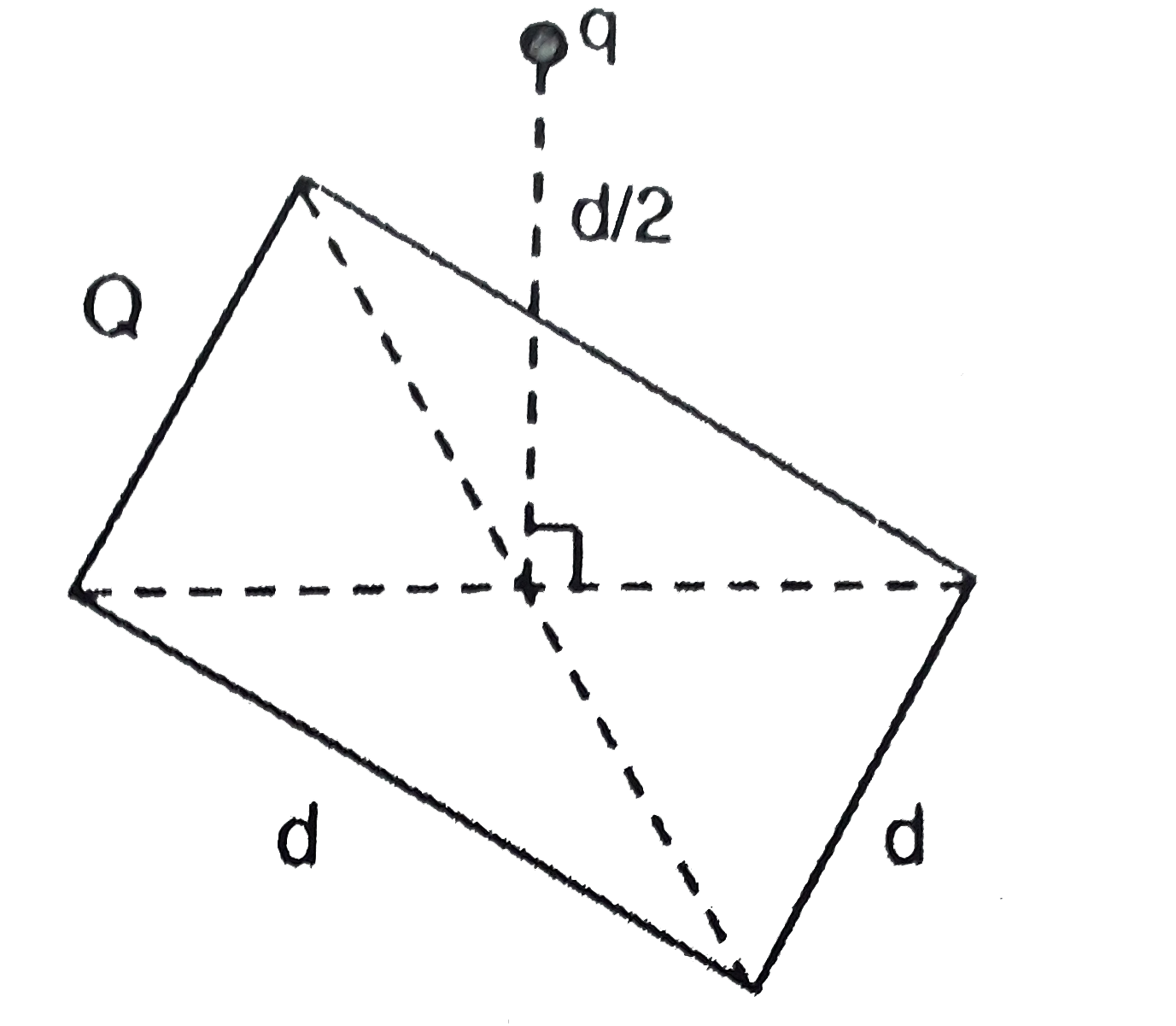
View SolutionTwo thin infinite parallel plates have uniform charge densities +σ and −σ. The electric field in the space between them is
View SolutionTwo large conducting plates of a parallel plate capacitor are given charges Q and 3Q respectively. If the electric field in the region between the plates is E0 , then the force of interaction between the plates is

View SolutionA point charge q is placed at the origin. Calculate the electric flux through the open hemispherical surface (x−a)2+y2+z2=a2,x≥a
View Solution
