A uniform rod lies at rest on a frictionless horizontal surface. A particle, having a mass equal to that of the rod, moves on the surface perpendicular to the rod collides with it, and finally sticks to it. The minimum loss of KE in the collision , under the given conditions, is
5%
10%
20%
30%
The correct Answer is:C
To solve the problem of a uniform rod colliding with a particle of equal mass and finding the minimum loss of kinetic energy (KE) in the collision, we can follow these steps:
Step 1: Define the system
Let the mass of the rod be m and the mass of the particle also be m. The rod is initially at rest, and the particle is moving with an initial velocity v perpendicular to the rod.
Step 2: Calculate the initial kinetic energy
The initial kinetic energy (KE_initial) of the system is solely due to the moving particle since the rod is at rest. Therefore, we can express the initial kinetic energy as:
KEinitial=12mv2
Step 3: Analyze the collision
Since the particle collides with the rod and sticks to it, this is an inelastic collision. After the collision, the combined mass of the rod and the particle will be 2m.
Step 4: Calculate the final velocity after collision
Using conservation of momentum, the momentum before the collision must equal the momentum after the collision. The initial momentum of the system is:
pinitial=mv
After the collision, the total momentum is:
pfinal=(2m)V
where V is the final velocity of the combined system. Setting the initial momentum equal to the final momentum gives:
mv=(2m)V
Solving for V:
V=v2
Step 5: Calculate the final kinetic energy
The final kinetic energy (KE_final) of the combined system is:
KEfinal=12(2m)V2=12(2m)(v2)2=12(2m)(v24)=mv24
Step 6: Calculate the loss of kinetic energy
The loss of kinetic energy during the collision can be calculated as:
Loss of KE=KEinitial−KEfinal=12mv2−mv24
Simplifying this expression:
Loss of KE=2mv24−mv24=mv24
Step 7: Find the minimum loss of KE
Thus, the minimum loss of kinetic energy in the collision is:
Minimum Loss of KE=mv24
Final Answer
The minimum loss of kinetic energy in the collision is mv24.
---
Let the mass of the rod be m and the mass of the particle also be m. The rod is initially at rest, and the particle is moving with an initial velocity v perpendicular to the rod.
The initial kinetic energy (KE_initial) of the system is solely due to the moving particle since the rod is at rest. Therefore, we can express the initial kinetic energy as:
KEinitial=12mv2
Since the particle collides with the rod and sticks to it, this is an inelastic collision. After the collision, the combined mass of the rod and the particle will be 2m.
Using conservation of momentum, the momentum before the collision must equal the momentum after the collision. The initial momentum of the system is:
pinitial=mv
After the collision, the total momentum is:
pfinal=(2m)V
where V is the final velocity of the combined system. Setting the initial momentum equal to the final momentum gives:
mv=(2m)V
Solving for V:
V=v2
The final kinetic energy (KE_final) of the combined system is:
KEfinal=12(2m)V2=12(2m)(v2)2=12(2m)(v24)=mv24
The loss of kinetic energy during the collision can be calculated as:
Loss of KE=KEinitial−KEfinal=12mv2−mv24
Simplifying this expression:
Loss of KE=2mv24−mv24=mv24
Thus, the minimum loss of kinetic energy in the collision is:
Minimum Loss of KE=mv24
The minimum loss of kinetic energy in the collision is mv24.
Similar Questions
A uniform rod of mass M and length L lies flat on a frictionless horizantal surface. Two forces F and 2F are applied along the length of the rod as shown. The tension in the rod at point P is
 View Solution
View Solution
A thin, uniform rod of mass M and length L is at rest on a smooth horizontal surface. A particle of same mass M collides with the rod at one end perpendicular to its length with velocity V∘ and sticks to it. C is the middle point of the rod and D is a point at a distance of L/4 from end A. the time taken by the rod turn through 90∘ after collisions.View SolutionA uniform rod of mass m and length L is at rest on a smooth horizontal surface. A ball of mass m, moving with velocity v0, hits the rod perpendicularly at its one end and sticks to it. The angular velocity of rod after collision is
 View Solution
View SolutionA uniform rod is resting freely over a smooth horizontal plane. A particle moving horizontally strikes at one end of the rod normally and gets stuck. Then
View Solution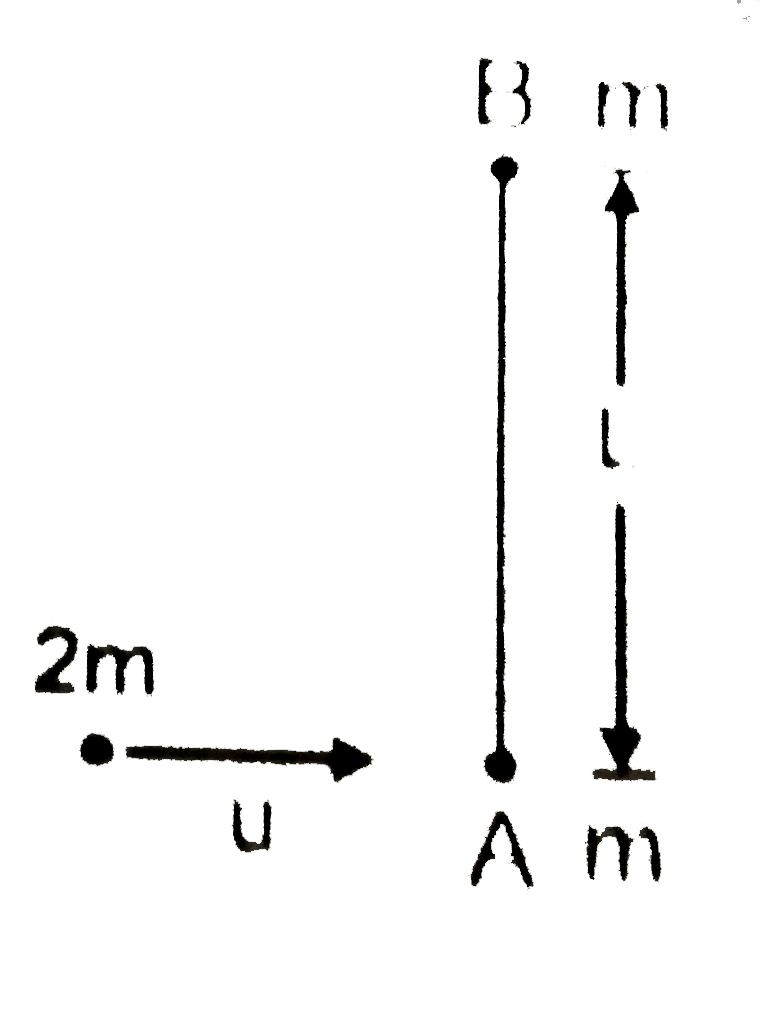
Two small balls A and B, each of mass m, are joined rigidly at the ends of a light rof of length L. they are placed on a frictionless horizontal surface another ball of mass 2 m moving with speed u towards one of the ball and perpendicular to the length of the rod on the horizontal frictionless surface as shown int he figure. if the coefficient of restitution is 1/2 then the angular speed of the rod after the collision will beView SolutionA uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
View SolutionA uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
View SolutionA uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View SolutionA uniform rod of length L rests on a frictionless horizontal surface. The rod is pivoted about a fixed frictionless axis at one end. The rod is initially at rest. A bulled travelling parallel to the horizontal surface and perpendicular to the rod with speed v strikes the rod at its centre and becomes embedded in it. the mass of the bullet is one-sixth the mass of the rod.
(a). What is the final angular velocity of the rod?
(b). What is the ratio of the kinetic energy of the system after the collision to the kinetic energy of te bullet the o collision?View SolutionA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the particle with respect to C before the collisionView Solution
