Figure shows the displacement of a particle going along the X-axis as a function of time. The force acting on the particle is zero in the region

The correct Answer is:18.5 m
Δt=t−0.6=0−10−4=2.5
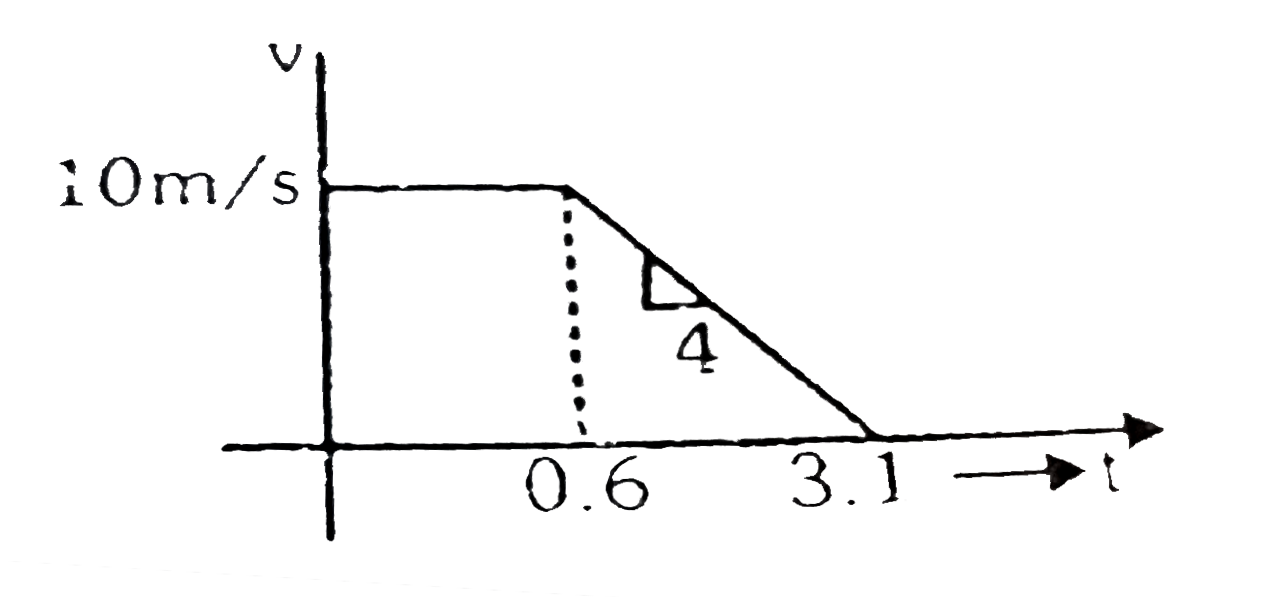
Stopping distance =0.6×10+12×2.5×10
6+12.5m=18.5m
Topper's Solved these Questions
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - Exercise-04[B]
14 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - Exercise-05 [A]
11 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - Comprehension#7
3 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
46 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
Similar Questions
Figure shows the displacement time graph of a particle moving on the X-axis

View SolutionFigure shows the displacement-time graph of a particle moving on the X-axis

View SolutionFigure shows the position of a particle moving on the X-axis as a function of time.

View SolutionFigure shows the position of a particle moving on the x - axis as a function of time
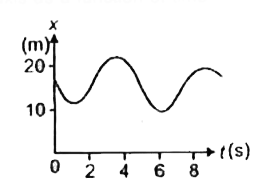
View SolutionFigure shows the graph of the x-coordinaste of a particle going along the X-axis as a function of time.Find a. te average velocity during 0 to 10s, b. instantaneous velocity at 2,5,8 and 12s.

View SolutionThe displacement of a particle along the x-axis is given by x=asin2ωt. The motion of the particle corresponds to
View SolutionThe displacement of a particle along the x- axis it given by x=asin2ωt The motion of the particle corresponds to
View SolutionFig. shows the graph of the x-coordinate of a particle going along the x-axis as a function of time. Find (a) the average velocity during 0 to 10s, (b) instantaneous velocity at 2, 5, 8 and 12s.

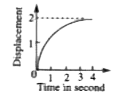
View SolutionThe displacement of a particle as a function of time is shown in . It indicates
 .
.
View SolutionThe displacement of a particle as a function of time is shown in the figure. The figure shows that
View Solution
