The time dependence of physical quantity p is given by p=p0 exp (−αt2), where α is a constant and t is the time. The constant α
The correct Answer is:A, B, C
Electric flux depends on the total charge enclosed by the closed surface S. Hence flux is related with charge Q1. Electric field at a point is the vector sum of the all electric field intensities due to all charges.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - Exercise-031videos
BASIC MATHS
- BOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - Exercise-041videos
BASIC MATHS
- BOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - Exercise-0124videos
BASIC MATHS
- BOOK - ALLENCHAPTER - AIIMS 2019EXERCISE - PHYSICS40videos
AIIMS 2019
- BOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)6videos
CIRCULAR MOTION
Similar Questions
The time dependence of a physical quantity P is given by P=P0exp(−αt2), where α is a constant and t is time. The constant α
View SolutionThe time dependence of a physical quantity P is given by P=P0exp(−αt2), where α is a constant and t is time. The constant α
View SolutionThe time dependence of a physical quantity P is given by P=P0e−αt2 , where α is a constant and t is time . Then constant α is//has
View SolutionThe time dependence of a physical quantity P is given by P=P0exp(∝t2), where ∝ is constant ∝ is represented as [M0LxT−2]. Find x
View SolutionIn the adjacent figure, the mutual inducatance of the infinite straight wire and the coil is M, while the self inductance of the coil is L. The current in infinite wire is varying according to the realtion l1=αt, where α is a constant and t is the time. The time dependence of current in the coil is
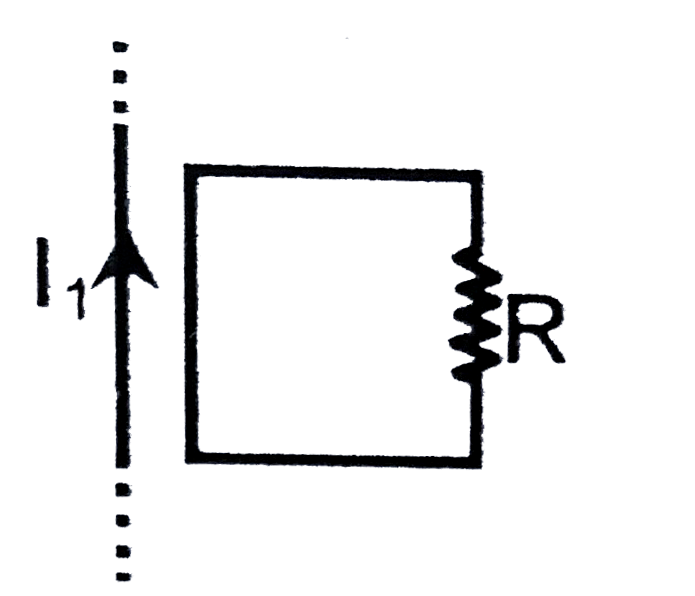 View Solution
View SolutionThe force of interaction between two atoms is given by F=αβexp(−x2αkt) , where x is the distance ,k is the Boltzmann constant and T is temperature and α and β are two constans. The dimension of β is :
View SolutionThe position of a particle at time t is given by the relation x(t)=(v0α)(1−c−at), where v0 is a constant and α>0. Find the dimensions of v0andα.
View SolutionThe position of a particle at time t is given by the relation x(t)=(v0α)(1−c−at), where v0 is a constant and α>0. Find the dimensions of v0andα.
View SolutionEnergy due to position of a particle is given by, U=α√yy+β, where α and β are constants, y is distance. The dimensions of (α×β) are
View SolutionIf force (F) is given by F=Pt−1+αt, where t is time. The unit of P is same as that of
View Solution
