Calculate the period of small oscillations of a floting box as shown in figure, which was pushed down inverical direction. The mass of box is m, area of its base is A and the density of liquid is ρ. The resistance of the liquid is assumed to be negligible.
_S01_033_Q01.png)
Initially when box is floating in liquid, if its h depth is sumerged in liquid then buoyancy force on it is
FB= weight of liquid displaced =Ahρg
_S01_033_S01.png)
As the box is in equilibrium, we have Ahρg=mg
Now if box is further pushed down by a distance x, net restorinn gorce ono it in upward (toward mean position) direction is
FB=−[A(h+x)ρg−mg]=−Axρg [ as mg=Ahρg]
It a is the accleration of box in upward direction we have a=−(Aρgm)x
Equation shows that the box executes SHM with angular frequency ω given as ω=√Aρgm
Thus time peiod of its equilibrium can be given as T=2πω=2π√mAρg
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - SOME WORKED OUT EXAMPLES
29 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-01
117 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
24 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
Determine the period of small oscillations of a mathematical pendulum, that is a ball suspended by a thread l=20cm in length, if it is located in a liquid whose density is η=3.0 times less than that of the ball. The resistance of the liquid is to be neglected.
View SolutionWhat would be the period of the free oscillations of the system shown here if mass M1 is pulled down a little force constant of the spring is k, mass of fixed pulley is negligible and movable pulley is smooth
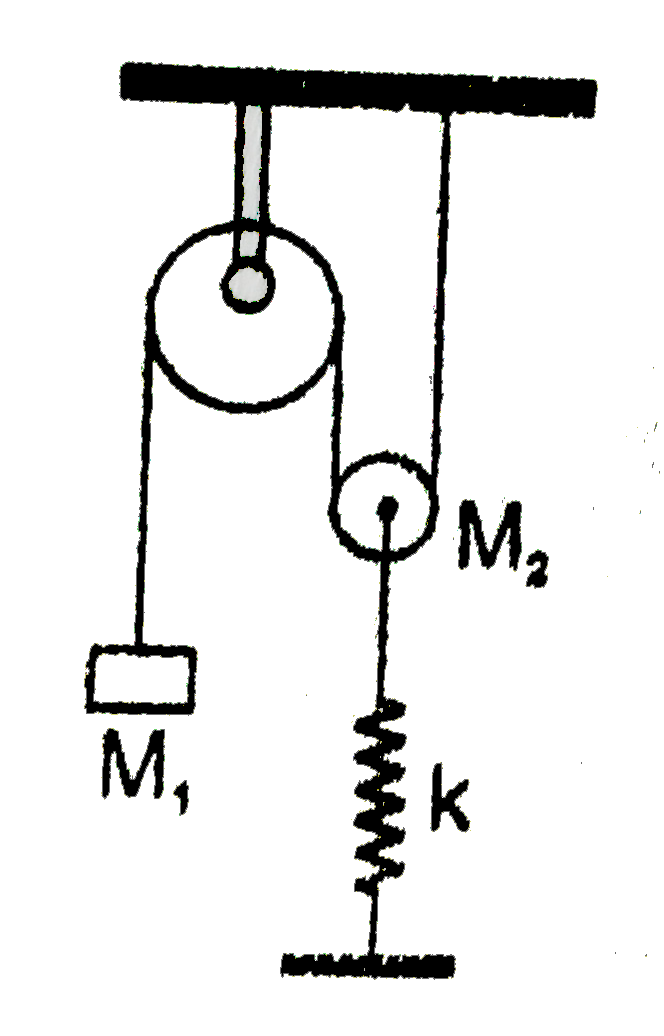
View SolutionA rectangular container moves with an acceleration a along the positive direction as shown in figure. The pressure at the A in excess of the atmospheric pressure p0 is (take ρ as the density of liquid)

View SolutionA uniform cube of mass M is floating on the surface of a liquid with three fourth of its volume immersed in the liquid (density=ρ). The length of the side of the cube is equal to

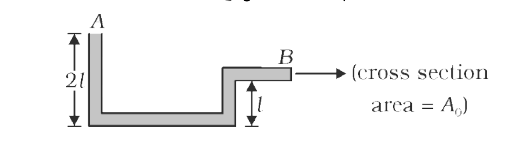
View SolutionA tube in vertical plane is shown in figure. It is filled with a liquid of density ρ and its end B is closed. Then the force exerted by the fluid on the tube at end B will be: [Assume the radius of the tube to be negligible in comparison to l]
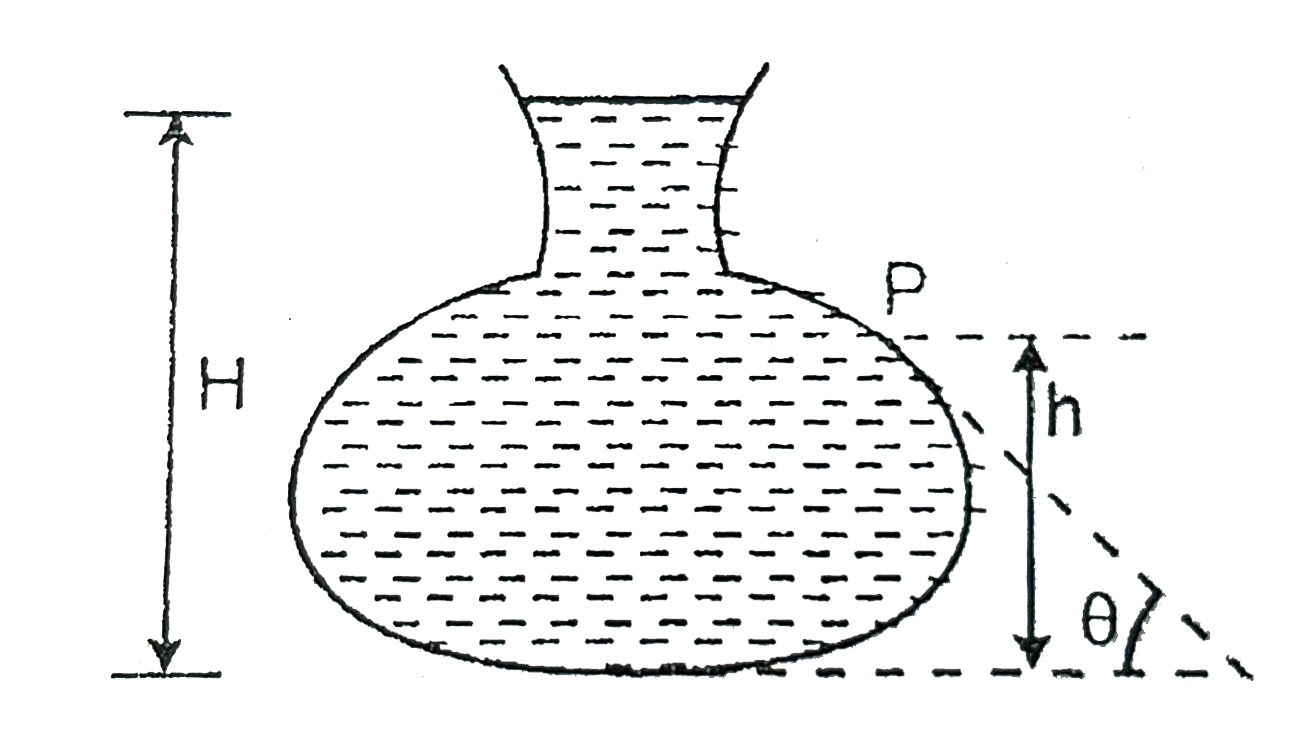
View SolutionFigure here shows the vertical cross-section of a vessel filled with a liquid of density ρ. The normal thrust per unit area on the walls vessel at point. P, as shown, will be
View SolutionA cylidrical vesel containing a liquid is closed by a smooth piston of mass m as shown in the figure. The area of cross section of the piston is A. If the atmospheric pressure is P0, find the pressure of the liquid just below the piston.
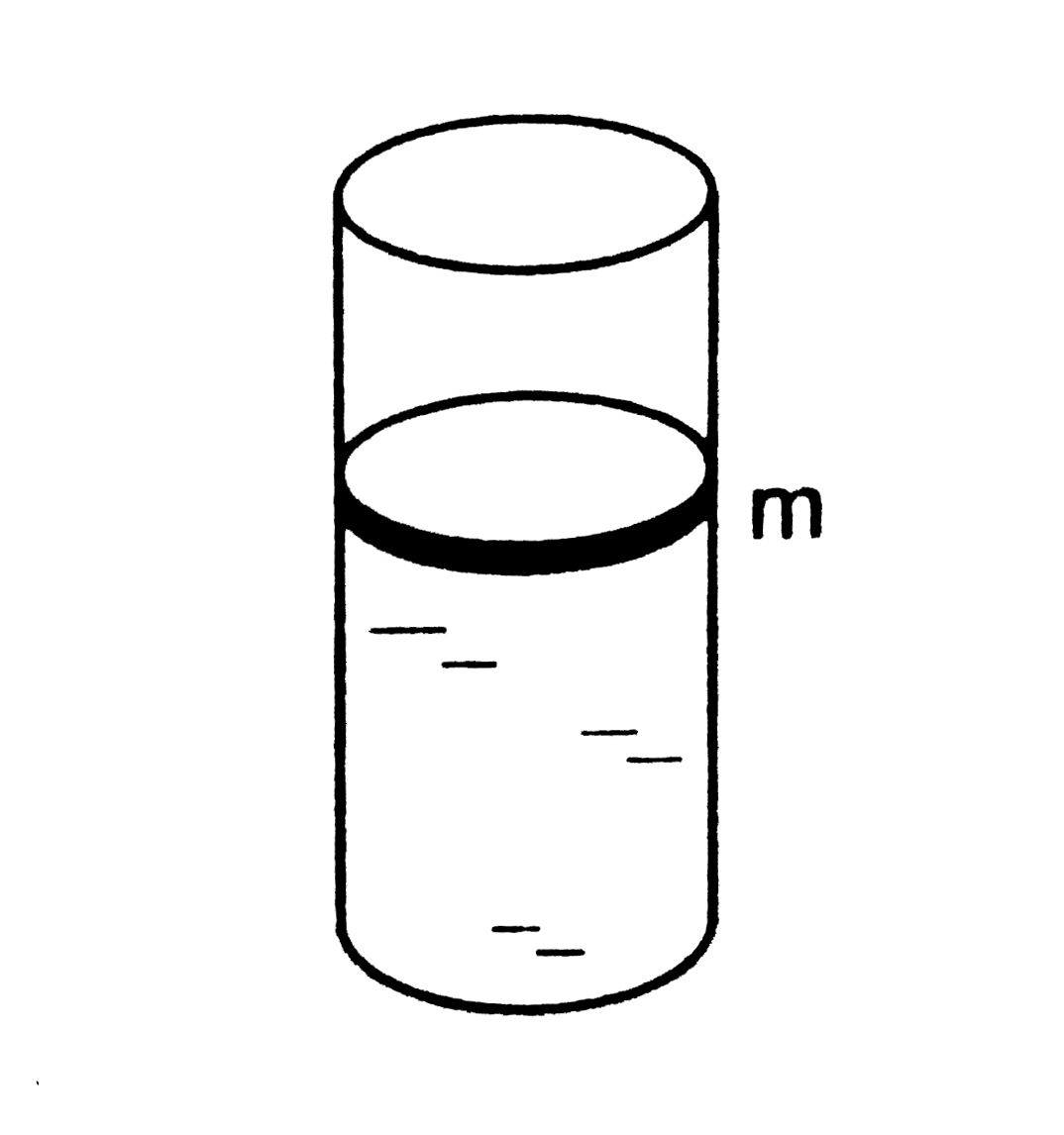 ,
,
View SolutionA cylindrical vessel containing a liquid is closed by a smooth piston of mass m as shown in the figure. The area of cross section of the piston is A. If the atmospheric pressure is P0, find the pressure of the liquid just below the piston.
 ,
,
View SolutionTwo vertical plates submerged partially in a wetting liquid form a wedge with a very small angle δφ. The edge of this wedge is vertical. The density of the liquid is ρ, its surface tension is α, the contact angle is θ. Find the height h, to which the liquid rises, as a function of the distance x from the edge.
View SolutionA non viscous liquid of density ρ is filled in a tube with A as the area of cross section, as shown in the figure. If the liquid is slightly depressed in one of the arms, the liquid column oscillates with a frequency

View Solution
