If one face of a prism angle 30∘andμ=√2 is silvered , the incident ray retraces its initial path. What is the angle of incidence?
To solve the problem step by step, we will analyze the situation involving the prism, the angle of incidence, and the refractive index.
1. Understanding the Prism Configuration:
- We have a prism with an angle of A=30∘.
- One face of the prism is silvered, which means it acts like a mirror for the light ray that hits it.
2. Incident Ray and Retracing Path:
- An incident ray strikes the prism and retraces its path after reflecting off the silvered surface.
- For the ray to retrace its path, it must strike the silvered face at an angle of incidence that allows it to reflect back along the same path.
3. Identifying Angles:
- Let the angle of incidence be I.
- The angle of refraction as the ray enters the prism can be denoted as R.
- The angle of reflection at the silvered face will also be R because the angle of incidence equals the angle of reflection.
4. Using Snell's Law:
- According to Snell's Law:
μ1sinI=μ2sinR
- Here, μ1=1 (for air) and μ2=√2 (for the prism).
5. Calculating the Angles:
- Since the prism angle A=30∘, and the ray retraces its path, the angle R can be determined using the geometry of the prism.
- The angle of refraction R can be found using the relationship:
R=A−I
- For the ray to retrace its path, it must reflect at 90∘ to the normal at the silvered face. Therefore, the angle of incidence I at the silvered face must be 90∘−R.
6. Setting Up the Equation:
- From the geometry, we can say:
R=90∘−I
- Substituting this into the equation A=R+I:
30∘=(90∘−I)+I
- This simplifies to:
30∘=90∘
- This is a contradiction, so we need to find R from the reflection condition.
7. Final Calculation Using Snell's Law:
- We know that:
√2sinR=sinI
- Given R=30∘:
sinR=sin30∘=12
- Therefore:
√2⋅12=sinI
- This gives us:
sinI=√22
- Thus, I=45∘.
Conclusion:
The angle of incidence I is 45∘.
- We have a prism with an angle of A=30∘.
- One face of the prism is silvered, which means it acts like a mirror for the light ray that hits it.
- An incident ray strikes the prism and retraces its path after reflecting off the silvered surface.
- For the ray to retrace its path, it must strike the silvered face at an angle of incidence that allows it to reflect back along the same path.
- Let the angle of incidence be I.
- The angle of refraction as the ray enters the prism can be denoted as R.
- The angle of reflection at the silvered face will also be R because the angle of incidence equals the angle of reflection.
- According to Snell's Law:
μ1sinI=μ2sinR
- Here, μ1=1 (for air) and μ2=√2 (for the prism).
- Since the prism angle A=30∘, and the ray retraces its path, the angle R can be determined using the geometry of the prism.
- The angle of refraction R can be found using the relationship:
R=A−I
- For the ray to retrace its path, it must reflect at 90∘ to the normal at the silvered face. Therefore, the angle of incidence I at the silvered face must be 90∘−R.
- From the geometry, we can say:
R=90∘−I
- Substituting this into the equation A=R+I:
30∘=(90∘−I)+I
- This simplifies to:
30∘=90∘
- This is a contradiction, so we need to find R from the reflection condition.
- We know that:
√2sinR=sinI
- Given R=30∘:
sinR=sin30∘=12
- Therefore:
√2⋅12=sinI
- This gives us:
sinI=√22
- Thus, I=45∘.
The angle of incidence I is 45∘.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - SOME WORKED OUT EXAMPLES
83 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -01
65 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
Knowledge Check
A ray of light is incident at 60∘ on one face of a prism of angle 30∘ and the emergent ray makes 30∘ with the incident ray. The refractive index of the prism is
A1.732B1.414C1.5D1.33
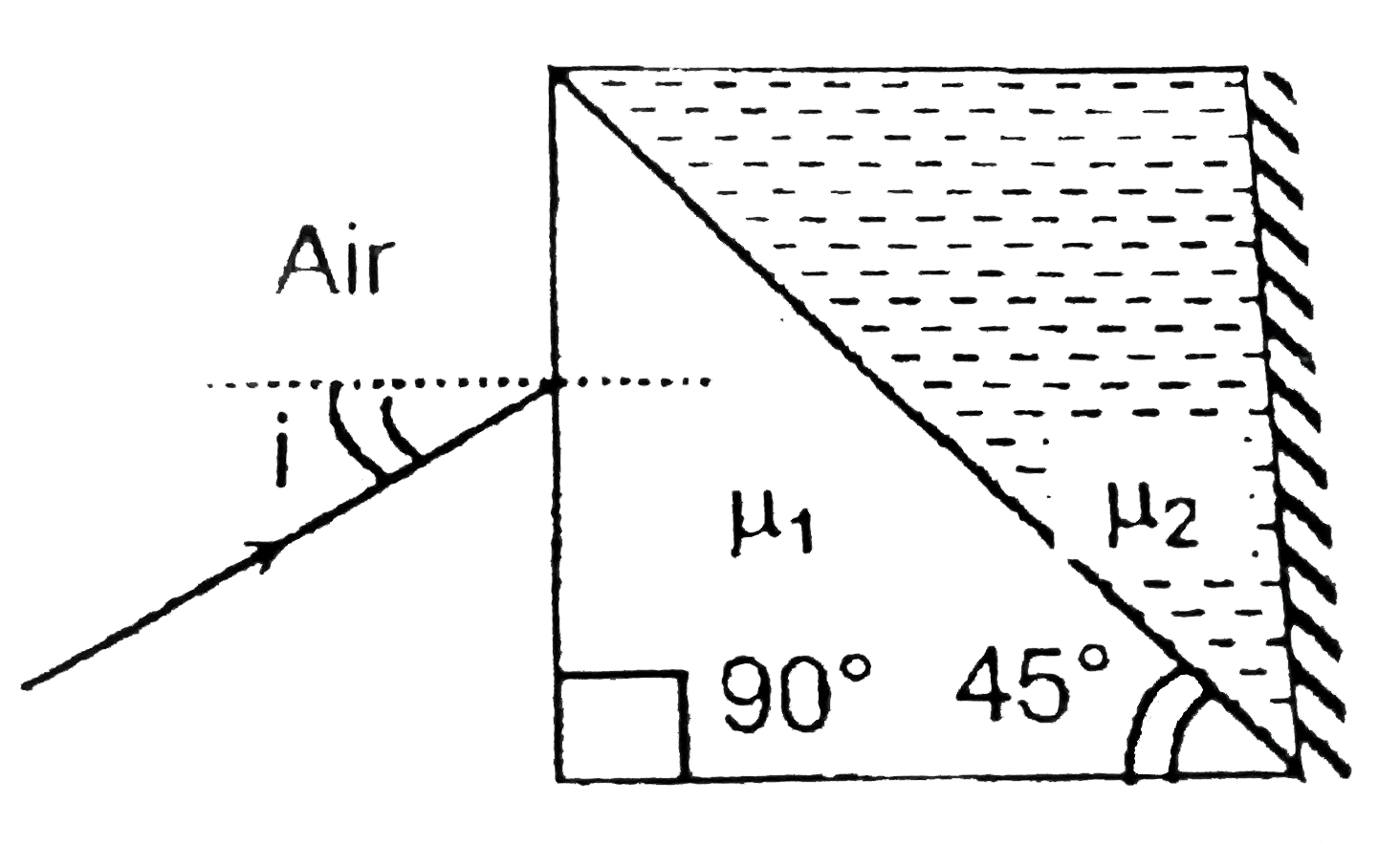
In the given situation, for what value of i, the incidence ray will retrace its initial path.
View SolutionA ray passes through a prism of angle 60∘ in minimum deviation position and suffers a deviation of 30∘. What is the angle of incidence on the prism
View SolutionOne face of a prism with a refrective angle of 30∘ is coated with silver. A ray of light incident on another face at an angle of 45∘ is refracted and reflected from the silver coated face and retraces its path. What is the refractive index of the prism?
View SolutionOne face of a prism with a refrective angle of 30∘ is coated with silver. A ray of light incident on another face at an angle of 45∘ is refracted and reflected from the silver coated face and retraces its path. What is the refractive index of the prism?
View SolutionA ray of light is incident at 65∘ on one face of a prism of angle of 30∘ and the emergent ray makes 35∘ with the incident ray. The refractive index of the prism is:
View SolutionA ray of light incident on an equilateral triangular glass prism of μ=√3 moves parallel to the base of the prism inside it. What is the angle of incidence for this ray ?
View SolutionA ray of light is incident at 60∘ on one face of a prism of angle 30∘ and the emergent ray makes 30∘ with the incident ray. The refractive index of the prism is
View Solution
