A particle with mass m and initial speed V0 is a subject to a velocity-dependent damping force of the form bVn.With dimensional analysis determine how the stopping time depends on m, V0 and b for begin with writing Δt=AmαbβVγ0, powers α,β and γ will be.
α=1,β=−1,γ=1−n
α=2−n,β=−1,γ=2
α=1,β=1,γ=1−n
α=−1,β=−1,γ=1−n
The correct Answer is:A
To determine how the stopping time (Δt) depends on mass (m), initial speed (V0), and the damping coefficient (b), we can use dimensional analysis. We start by expressing Δt in terms of these variables:
Δt=AmαbβVγ0
where A is a dimensionless constant, and α, β, and γ are the powers we need to find.
Step 1: Identify the dimensions of each variable
- Mass (m): The dimension is (M1L0T0)
- Damping coefficient (b): The damping force is given by F=bVn. The dimensions of force (F) are (M1L1T−2), and the dimensions of velocity (V) are (L1T−1). Thus, we can express b in terms of dimensions:
(b)=(F)(Vn)=(M1L1T−2)(L1T−1)n=(M1L1−nT−2+n)
- Initial speed (V0): The dimension is (L1T−1)
Step 2: Write the dimensions of Δt
The dimension of time (Δt) is (M0L0T1).
Step 3: Substitute the dimensions into the equation
Now we substitute the dimensions into the equation:
(M0L0T1)=(M1L0T0)α(M1L1−nT−2+n)β(L1T−1)γ
This expands to:
(M0L0T1)=(Mα+βLβ(1−n)+γTβ(−2+n)−γ)
Step 4: Set up equations for each dimension
Now we can equate the powers of M, L, and T:
1. For mass (M):
α+β=0(1)
2. For length (L):
β(1−n)+γ=0(2)
3. For time (T):
β(−2+n)−γ=1(3)
Step 5: Solve the equations
From equation (1):
β=−α
Substituting β=−α into equation (2):
(−α)(1−n)+γ=0⟹γ=α(n−1)
Substituting β=−α and γ=α(n−1) into equation (3):
(−α)(−2+n)−α(n−1)=1
α(2−n)−α(n−1)=1
α(2−n−n+1)=1⟹α(3−2n)=1⟹α=13−2n
Now substituting α back to find β and γ:
β=−13−2n,γ=13−2n(n−1)
Final Result
Thus, the powers are:
- α=13−2n
- β=−13−2n
- γ=n−13−2n
The final expression for stopping time is:
Δt=Am13−2nb−13−2nVn−13−2n0
- Mass (m): The dimension is (M1L0T0)
- Damping coefficient (b): The damping force is given by F=bVn. The dimensions of force (F) are (M1L1T−2), and the dimensions of velocity (V) are (L1T−1). Thus, we can express b in terms of dimensions:
(b)=(F)(Vn)=(M1L1T−2)(L1T−1)n=(M1L1−nT−2+n)
The dimension of time (Δt) is (M0L0T1).
Now we substitute the dimensions into the equation:
Now we can equate the powers of M, L, and T:
α+β=0(1)
β(1−n)+γ=0(2)
β(−2+n)−γ=1(3)
From equation (1):
β=−α
(−α)(1−n)+γ=0⟹γ=α(n−1)
(−α)(−2+n)−α(n−1)=1
α(2−n)−α(n−1)=1
α(2−n−n+1)=1⟹α(3−2n)=1⟹α=13−2n
β=−13−2n,γ=13−2n(n−1)
Thus, the powers are:
- α=13−2n
- β=−13−2n
- γ=n−13−2n
Δt=Am13−2nb−13−2nVn−13−2n0
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exersice-037videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - ASSERTION-REASON18videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Part -II Example Some worked out Examples1videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-78videos
KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
- BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV8videos
PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT
Similar Questions
A particle moves with an initial velocity V0 and retardation αv , where α is a constant and v is the velocity at any time t.
After how much time, speed of particle decreases by 75%View SolutionA particle moves with an initial velocity V0 and retardation αv , where α is a constant and v is the velocity at any time t.
Velocity of particle at time is :View SolutionA particle moves with an initial velocity V0 and retardation αv , where α is a constant and v is the velocity at any time t.
total distance covered by the particle isView SolutionA particle of mass m is at rest at the origin at time t=0 It is subjected to a force F(t)=F0e−bt in the X-direction. Its speed V(t) is depicted by which of the following curves
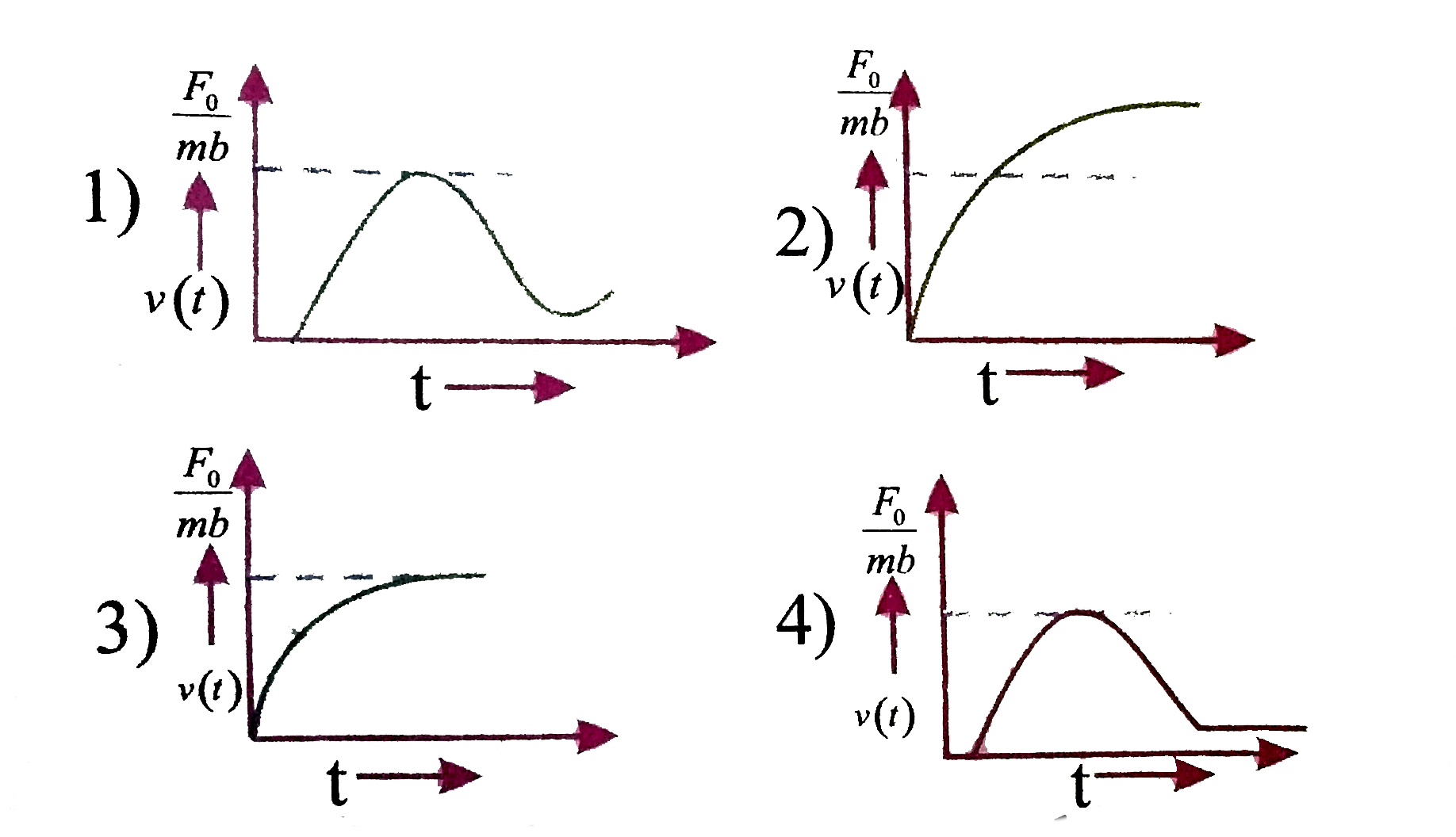View SolutionA particle of mass m is at rest the origin at time t=0 . It is subjected to a force F(t)=F0e−bt in the x - direction. Its speed v(t) is depicted by which of the following curves ?
View SolutionA particle of mass m, moving in a circle of radius R, has a velocity v=v0(1−e−γt) The power delivered to tha particle by the force at t=0 is
View SolutionA particle of spectfic charge α enters a uniform magnetic field B=−B0ˆk with velocity V=v0ˆi from the origin Find the time dependence of velocity and position of the particle
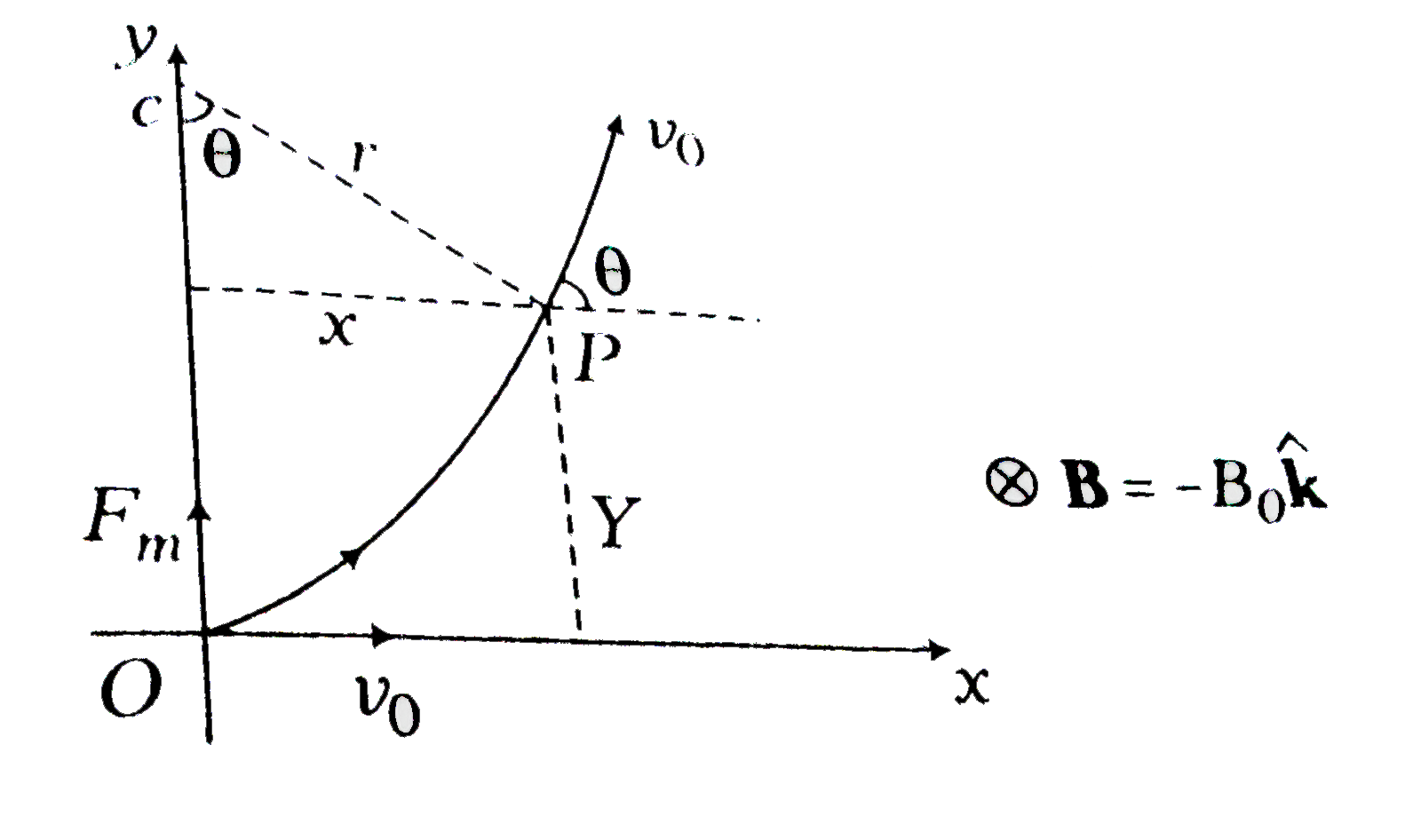
View SolutionA particle of specific charge alpha enters a uniform magnetic field B=−B0ˆk with velocity v=v0ˆi from the origin. Find the time dependence of velocity and position of the particle.
View SolutionA particle of mass m and positive charge q is projected with a speed of v0 in y–direction in the presence of electric and magnetic field are in x–direction. Find the instant of time at which the speed of particle becomes double the initial speed.
View SolutionA particle of mass m moves along the internal smooth surface of a vertical cylinder of the radius R. Find the force with which the particle acts on the cylinder wall if at the initial moment of time its velocity equals v0. And forms an angle α with the horizontal.
View Solution