For shown situation find the maximum elongation in the spring. Neglect friction everywhere. Initiallthe blocks are at rest and spring is unstreched.
A.
B.
C.
D.
The correct Answer is:(A)
To find the maximum elongation in the spring when the blocks are at rest and the spring is unstretched, we can use the concept of reduced mass and the work-energy theorem. Here’s a step-by-step solution:
Step 1: Understand the System
We have a system of blocks connected by a spring. Initially, the blocks are at rest, and the spring is unstretched. We need to find the maximum elongation of the spring when a force F is applied.
Step 2: Define the Reduced Mass
For a system of two masses m1 and m2, the reduced mass μ is given by the formula:
μ=m1m2m1+m2
In our case, let’s assume we have three blocks of mass 2m, 3m, and 6m. We will consider the two blocks with masses 3m and 6m for calculating the reduced mass.
Step 3: Calculate the Reduced Mass
Using the formula for reduced mass:
μ=3m⋅6m3m+6m=18m29m=2m
Step 4: Apply Newton's Second Law
The net force acting on the system can be expressed as:
Fnet=F−Fspring
Where Fspring is the force exerted by the spring when it is elongated by x.
Step 5: Use Work-Energy Theorem
According to the work-energy theorem, the work done on the system is equal to the change in kinetic energy. In our case, the work done by the applied force F is equal to the potential energy stored in the spring:
W=12kx2
Where k is the spring constant and x is the elongation of the spring.
Step 6: Set Up the Equation
The work done by the force can also be expressed as:
W=F⋅d
Where d is the distance moved by the center of mass. Here, we can express the work done as:
F⋅x=12kx2
Step 7: Solve for Maximum Elongation
From the forces acting on the blocks, we can set up the equation:
2F3⋅x=12kx2
Rearranging gives:
kx2−4F3x=0
Factoring out x:
x(kx−4F3)=0
Thus, the maximum elongation x can be found as:
kx=4F3⟹x=4F3k
Conclusion
The maximum elongation in the spring is:
x=4F3k
Thus, the correct answer is option A: 4F3K.
We have a system of blocks connected by a spring. Initially, the blocks are at rest, and the spring is unstretched. We need to find the maximum elongation of the spring when a force F is applied.
For a system of two masses m1 and m2, the reduced mass μ is given by the formula:
μ=m1m2m1+m2
In our case, let’s assume we have three blocks of mass 2m, 3m, and 6m. We will consider the two blocks with masses 3m and 6m for calculating the reduced mass.
Using the formula for reduced mass:
μ=3m⋅6m3m+6m=18m29m=2m
The net force acting on the system can be expressed as:
Fnet=F−Fspring
Where Fspring is the force exerted by the spring when it is elongated by x.
According to the work-energy theorem, the work done on the system is equal to the change in kinetic energy. In our case, the work done by the applied force F is equal to the potential energy stored in the spring:
W=12kx2
Where k is the spring constant and x is the elongation of the spring.
The work done by the force can also be expressed as:
W=F⋅d
Where d is the distance moved by the center of mass. Here, we can express the work done as:
F⋅x=12kx2
From the forces acting on the blocks, we can set up the equation:
2F3⋅x=12kx2
Rearranging gives:
kx2−4F3x=0
Factoring out x:
x(kx−4F3)=0
Thus, the maximum elongation x can be found as:
kx=4F3⟹x=4F3k
The maximum elongation in the spring is:
x=4F3k
Thus, the correct answer is option A: 4F3K.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I
40 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II
43 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
A block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unsrtretched when a constnt force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View SolutionA block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is upstretched when a constant force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View SolutionA block of mass 'm' is connected to another block of mass 'M' by a spring (massless) of spring constant 'k' The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched Then a constant force 'F' starts acting on the block of mass 'M' to pull it. Find the force on the block of mass 'm' :
View SolutionA block of mass 1kgis placed on a rough horizontal surface. A spring is attached to the block whose other end is joined to a rigid wall, as shown in the figure. A horizontal force is applied on the block so that it remains at rest while the spring is elongated by x(x≥μmgk). Let Fmax and Fmin be the maximum and minimum values of force F for which the block remains in equilibrium. For a particular x,Fmax−Fmin=2N. Also shown is the variation of Fmax+Fmin versus x, the elongation of the spring.
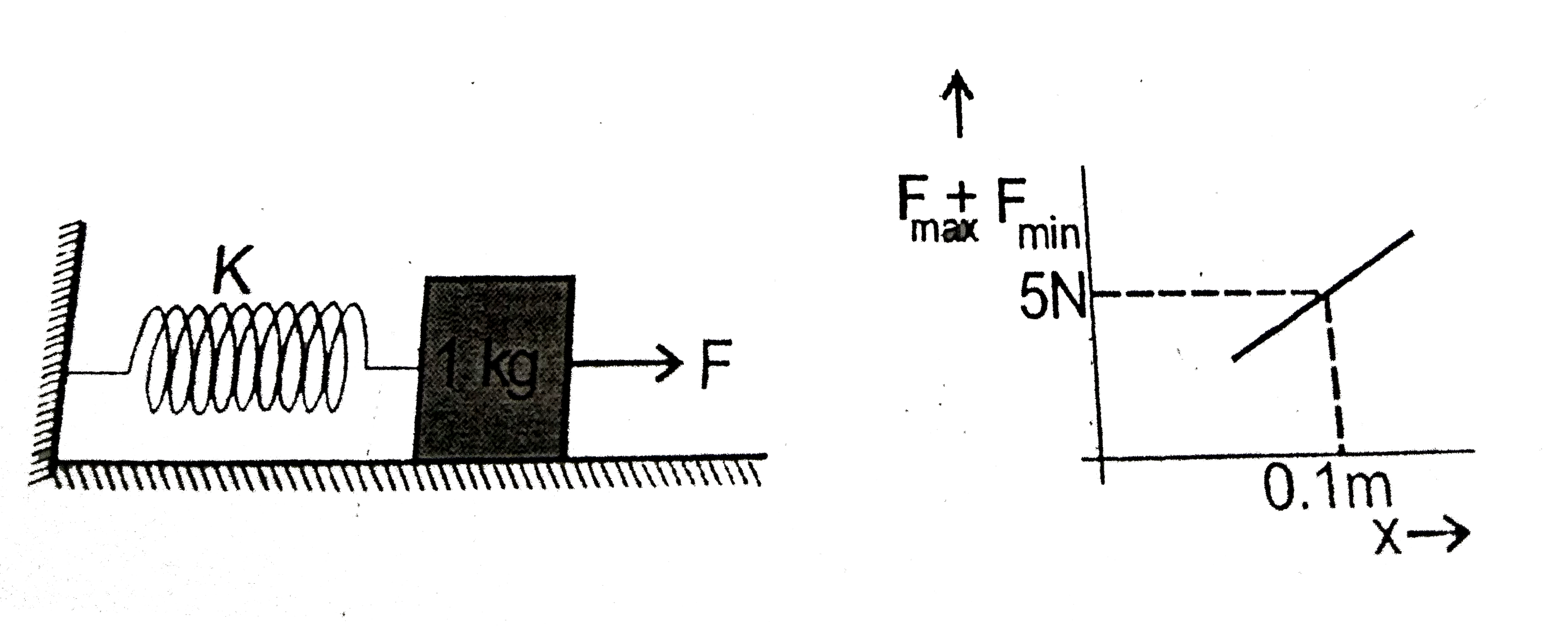
The coefficient of friction between the block and the horizontal surface is :
View SolutionIn figure, the stiffness of the spring is k and mass of the block is m. The pulley is fixed. Initially, the block m is held such that the elongation in the spring is zero and then released from rest. Find:
a. the maximum elongation in the spring.
b. the maximum speed of the block m. Neglect the mass of the spring and that of the string. Also neglect the friction.
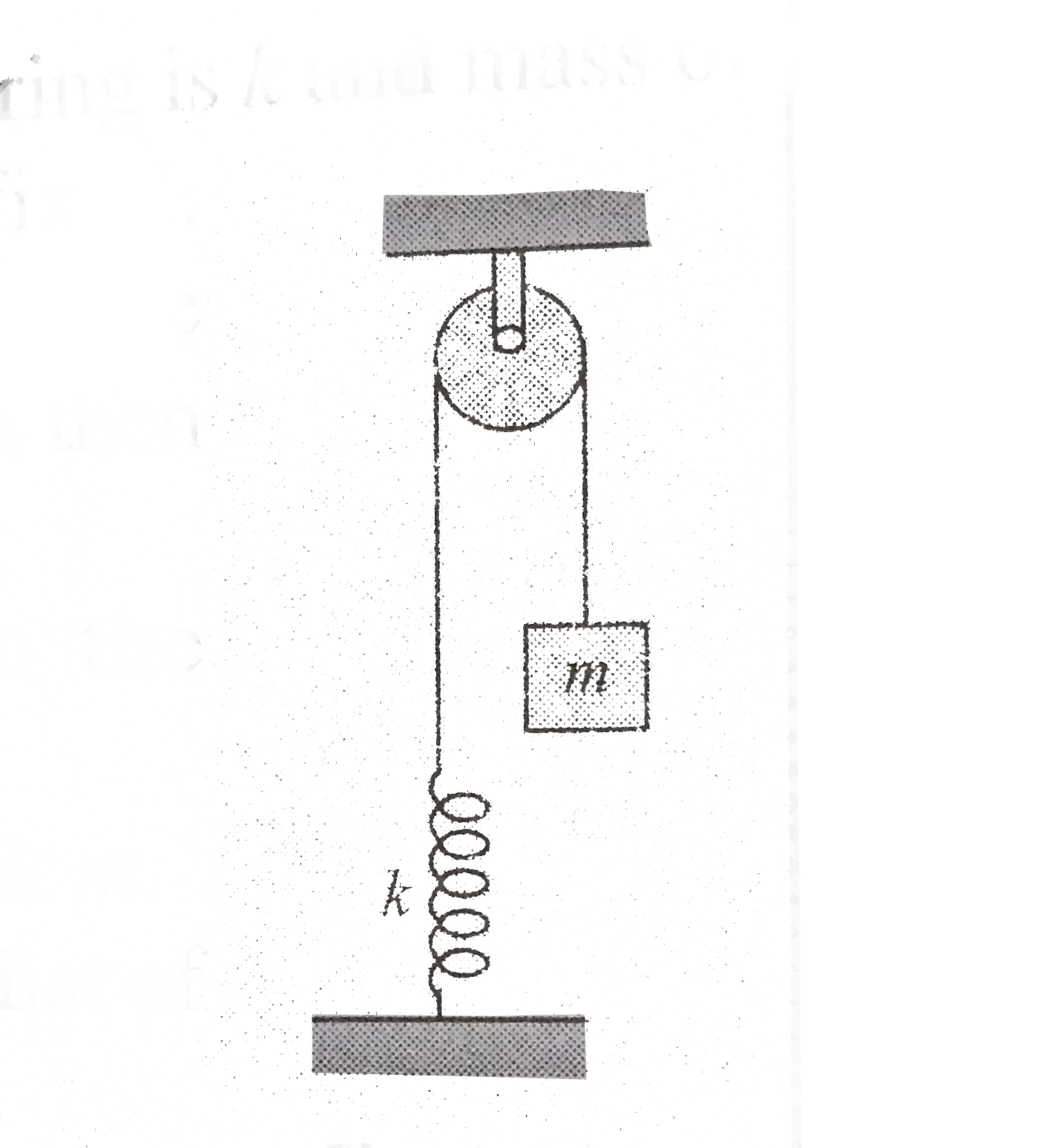
View SolutionA block of mass 1kgis placed on a rough horizontal surface. A spring is attached to the block whose other end is joined to a rigid wall, as shown in the figure. A horizontal force is applied on the block so that it remains at rest while the spring is elongated by x(x≥μmgk). Let Fmax and Fmin be the maximum and minimum values of force F for which the block remains in equilibrium. For a particular x,Fmax−Fmin=2N. Also shown is the variation of Fmax+Fmin versus x, the elongation of the spring.
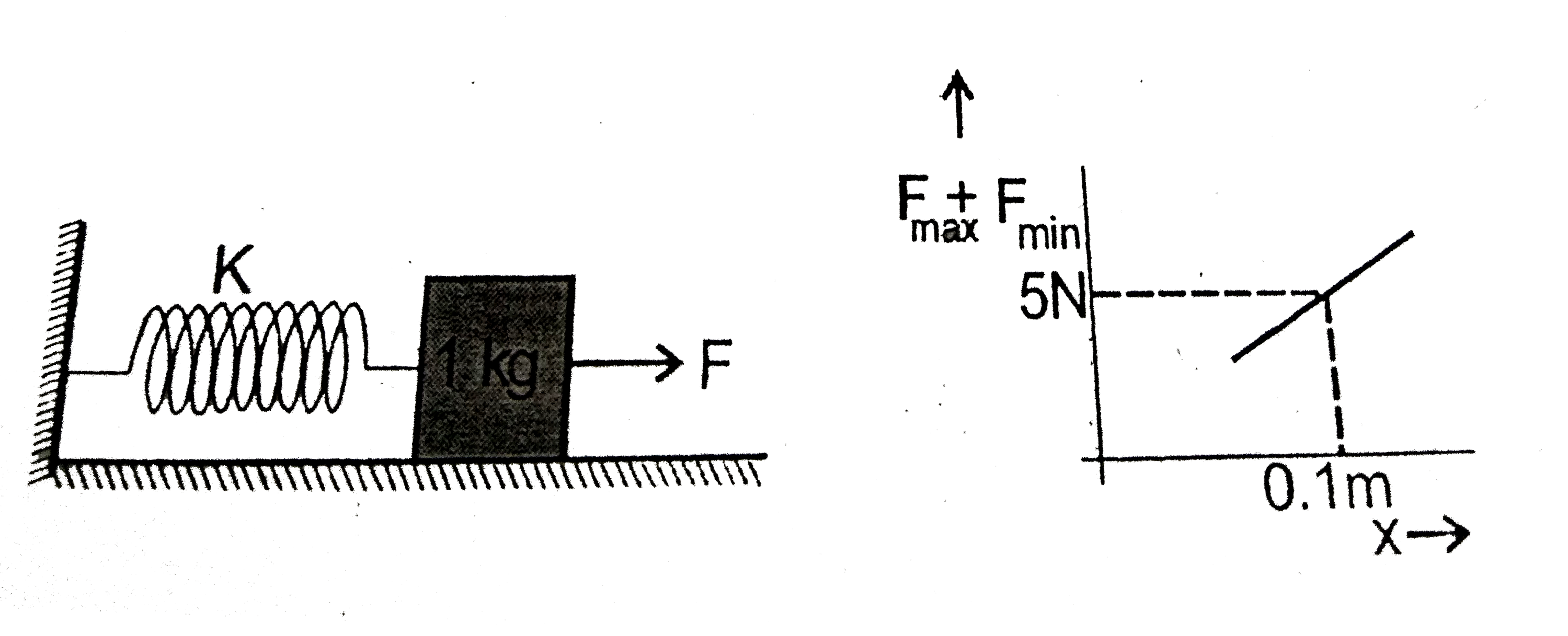
The spring constant of the spring is :
View SolutionA block of mass 1kgis placed on a rough horizontal surface. A spring is attached to the block whose other end is joined to a rigid wall, as shown in the figure. A horizontal force is applied on the block so that it remains at rest while the spring is elongated by x(x≥μmgk). Let Fmax and Fmin be the maximum and minimum values of force F for which the block remains in equilibrium. For a particular x,Fmax−Fmin=2N. Also shown is the variation of Fmax+Fmin versus x, the elongation of the spring.
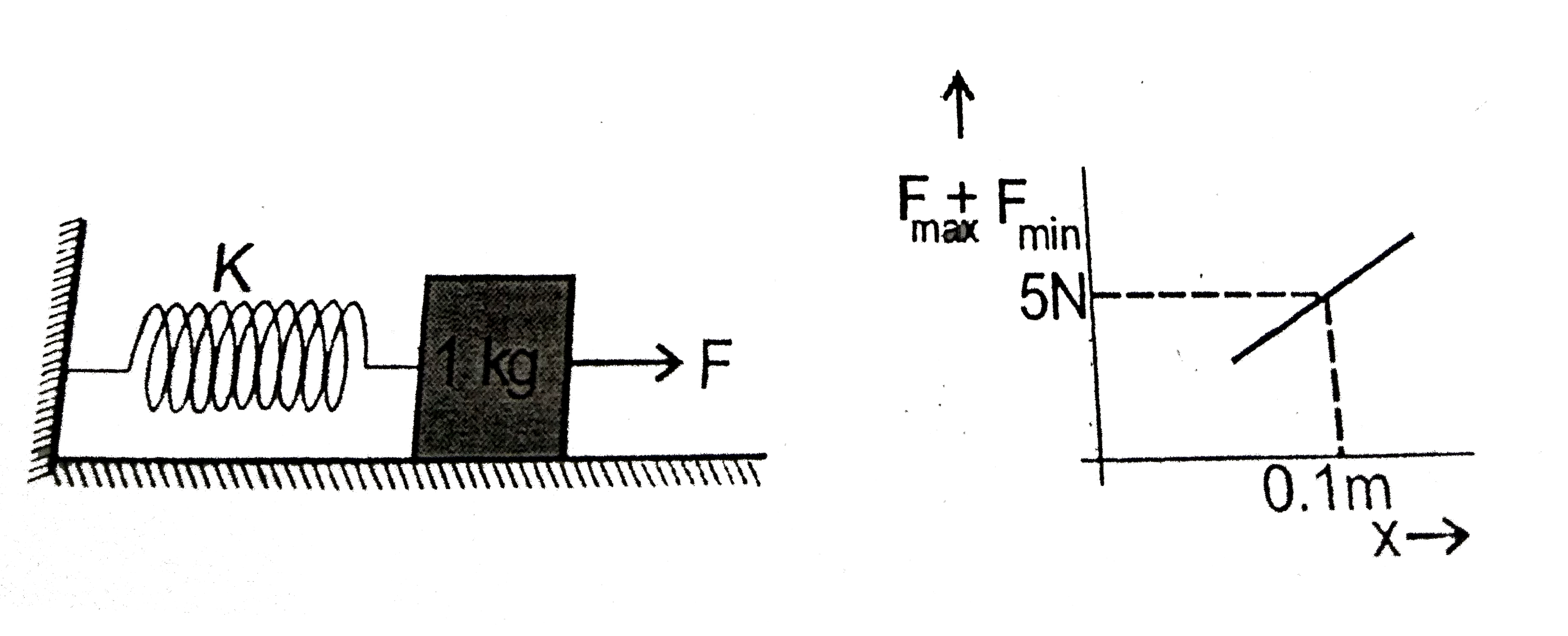
The value of Fmin, if x=3cm is :
View SolutionConsider the situation shown in figure.
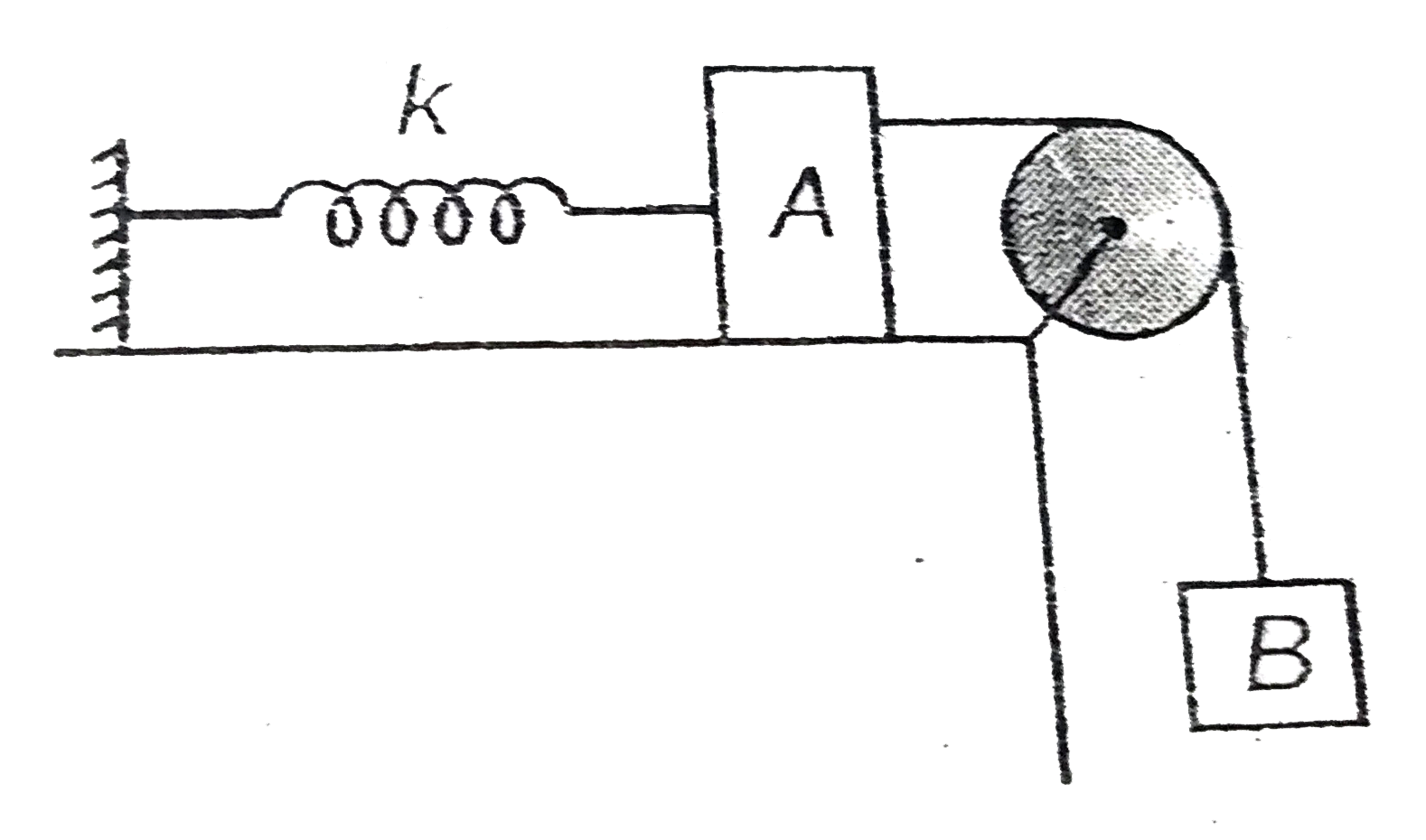
Mass of block A is m and that of blcok B is 2m. The force constant of string is k. Friction is absent everywhere. System is released from rest with the spring unstretched. Find
(a) The maximum extension of the spring xm
(b) The speed of block A when the extension in the springt is x=xm2
(c ) The net acceleration of block B when extension in the spring is x=xm4.
View SolutionA block of mass m=2kg is connected to a a spring of force constant k=50N/m. Initially the block is at rest and tlhe spring has natural length. A constant force F=60N is applied horizontally towards, the maximum speed of the block (in m/s) will be (negelect friction).

View SolutionA constant force F is applied on a spring block system as shown in figure. The mass of the block is m and spring constant is k. The block is placed over a smooth surface. Initially the spring was unstretched. Choose the correct alternative(s)

View Solution
