The wooden plank of length 1 m and uniform cross section is hinged at one end to the bottom of a tank as shown in figure. The tank is filled with water up to a height of 0.5 m. The specific gravity of the plank is 0.5. Find the angle that the plank makes with the vertical in the equilibrium position. (Exclude the case )
 ,
,
The forces acting om the plank are shown in the figure. The height of water gravity of the plank is 0.5. Find the angle 0 the pank 1.0=2l. The weight of the plank acts throught he centre B of the plank. We have The buoyant force F acts through the point A which is the middle point of the dipped part OC of the plank.
We have
Let the mass per unit length of the plank be . its weight .
The mass of the part OC of the plank .
the mass of water displaced
The buoyant force F is therefore
Now, for equilibrium the torque of mg about O should balance the torque of F about O.
So, mg or , or, or , or
Topper's Solved these Questions
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 1 (Elasticity)
16 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 1 (Surface Tension)
21 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- ERROR AND MEASUREMENTBOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
Similar Questions
A wooden plank of length 1m and uniform cross-section is hinged at one end to the bottom of a tank as shown in fig. The tank is filled with water upto a hight 0.5m. The specific gravity of the plank is 0.5. Find the angle θ that the plank makes with the vertical in the equilibrium position. (Exclude the case θ=θ∘)

View SolutionA wooden rod of a uniform cross section and of length 120cm is hinged at the bottom of the tank which is filled with water to a height of 40cm. In the equilibrium position, the rod makes an angle of 60∘ with the vertical. The centre of buoyancy is located on the rod at a distance (from the hinge) of
View Solution
Knowledge Check
A liquid of density ρ0 is filled in a wide tank to a height h. A solid rod of length L, cross-section A and density ρ is suspended freely in the tank. The lower end of the rod touches the base of the tank and h=L/n (where n gt 1). Then the angle of inclination θ of the rod with the horizontal in equilibrium position is
Asin−1(√ρ0ρ)Bsin−1(n√ρ0ρ)Csin−1(1n√ρ0ρ)Dsin−1(1n√ρρ0)
A tank of square cross section (2m×2m) is filled with water up to a height of 2.5m. Find the thrust experienced by the vertical and botom of the tank (g=10m/s2).
View SolutionA uniform rod of length 2.0 m specific gravity 0.5 and mass 2 kg is hinged at one end to the bottom of a tank of water (specific gravity = 10) filled upto a height o f 1.0 m as shown in figure. Taking the case θ=−0∘ the force exerted by the hings on the rod is (g=10m/s2)
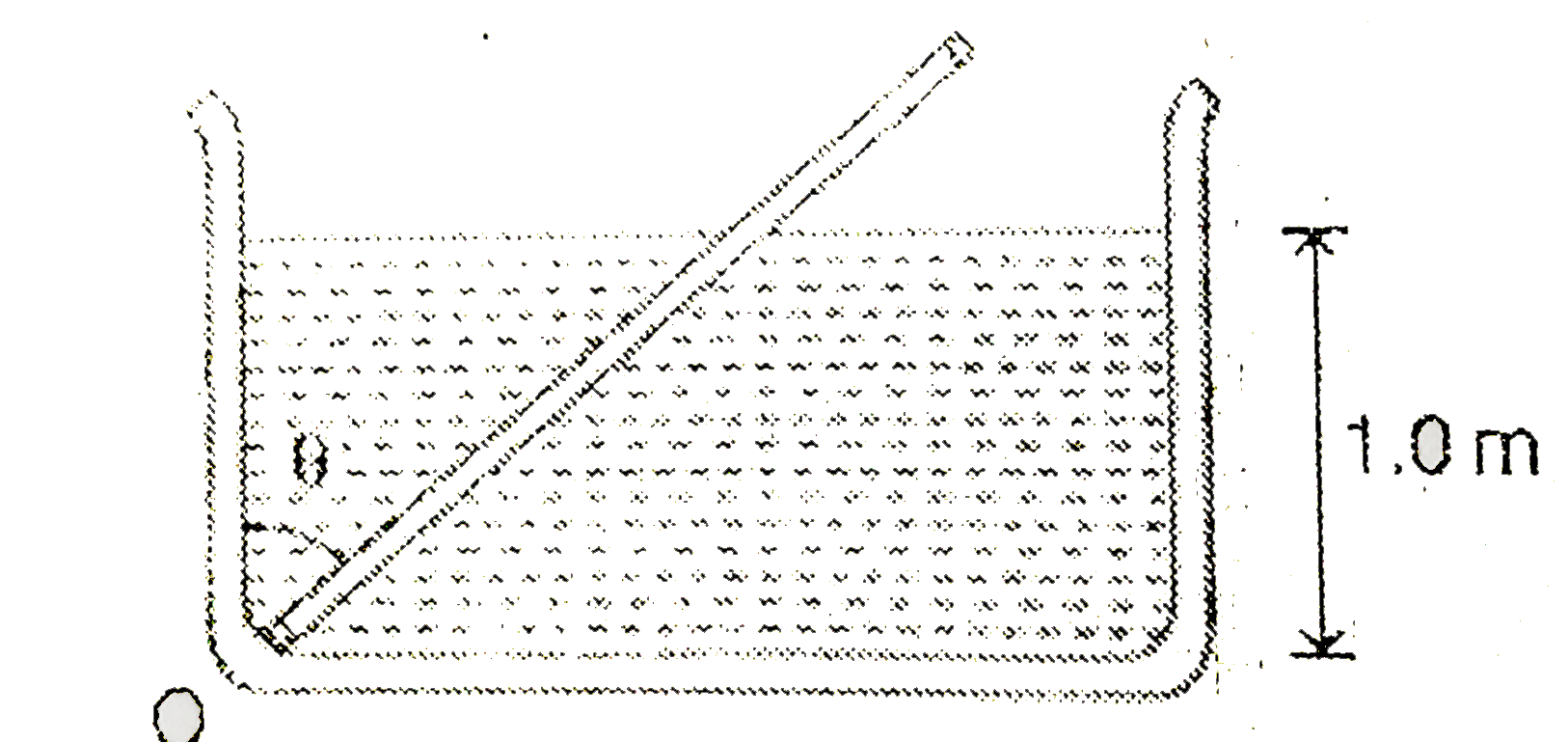
View SolutionA uniform rod of length L pivoted at the bottom of a pond of depth L/2 stays in stable equilibrium as shown in the figure.

Find the angle 0 if the density of the material of the rod is half of the density of water.
View SolutionA uniform wooden bar of length l and mass m hinged on a vertical wall of a containing water, at one end.

3/5th part of the bar is submerged in water. Find the ratio of densities of the liquid and the bar.
View SolutionA tank 5 m high is half filled with water and then is filled to top with oil of density 0.85g/cm3 The pressure at the bottom of the tank, due to these liquids is
View Solution_S01_067_Q01.png)
A solid right cylinder of length l stands upright at rest on the bottom of a large tub filled with water up to height h as shown in the figure-I density of material of the cylinder equals to that of water. Now the cylinder is pulled slowly out of water with the help of a thin light inextensible thread as shown in figure-II. Find the work done by the tension force develop in the thread.
(a). mgh
(b). mgl
(c). 0.5 mgl
(d). mg(0.5l+h)
View SolutionA cylinderical tank of height 0.4 m is open at the top and has a diameter 0.16m. Water is filled in it up to height of 0.16 m. Find the time taken to empty the tank through a hole of radius 5×10−3m in its bottom.
View Solution
