Show that the electric field intensity at a point in an electric field is equal to the negative of the potential gradient of the field at that point.
Solution in Punjabi
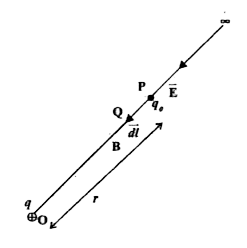
Let us consider a point charge +q located at O, as shown in Fig. Supposė at any instant the test charge is at a point P such that
. Let be the electric field at P due to charge + q. So the force on the test charge
is . Hence an external force is required to displace the test charge against the field.
In displacing the test charge through a small displacement , one needs to do a small amount of work, given by
If the test charge is moved from A to B, total work done is given by
The work done in moving a unit positive charge from A to B, or by definition, the potential difference between points A and B will be
That is, the potential difference between two points A and B is equal to the negative of the line integral of the electrostatic field along the path AB.
If point A at infinity, where potential , the potential at point B is given by
Potential at any point with position vector is
Thus, the electric potential at any point is equal to the negative of the line integral of the electrostatic field from infinity to that point.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIALBOOK - BETTER CHOICE PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIALEXERCISE - NUMERICAL PROBLEMS (MOST EXPECTED QUESTIONS)
6 Videos
- ELECTROSTATIC POTENTIALBOOK - BETTER CHOICE PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIALEXERCISE - MOST EXPECTED QUESTIONS (2 Marks Questions)
4 Videos
- ELECTRONIC DEVICES SOLIDSBOOK - BETTER CHOICE PUBLICATIONCHAPTER - ELECTRONIC DEVICES SOLIDSEXERCISE - Most Expected Questions
9 Videos
- FORCE ON A CHARGE BOOK - BETTER CHOICE PUBLICATIONCHAPTER - FORCE ON A CHARGE EXERCISE - NUMERICAL PROBLEMS
14 Videos
Similar Questions
Calculate the electric potential at the surface of a gold nucleus. Given radius of nucleus = 6.6×10−15m and atomic wight of gold is 79.
View SolutionDraw an equipotential surface for a system consisting of two charges Q, -Q separated by a distance r in air.
View SolutionWhy semiconductors are doped?
View SolutionAn electron (with charge 1.6×10−19C) moving at right angles to a uniform magnetic field completes a circular orbit in 10−6sec. Calculate the vlaue of magnetic field. Given mass of electron =9×10−31kg.
View Solutionसिद्ध कीजिए की विद्युत-क्षेत्र के किसी बिन्दु पर विद्युत-क्षेत्र की तीव्रता उस बिन्दु पर दुरी के साथ विभव परिवर्तन की दर के ऋणात्मक मान के बराबर होती है |
View SolutionShow that the electric field intensity at a point can be given as negative of potential gradient.
View SolutionDefine electric dipole. Show that the electric field is the negative gradient of its potential.
View SolutionEstablish relation between electric field and potential gradient. Or Derive relationship between Electric field intensity and potential gradient at a point in the electric field.
View SolutionProve that electric field at a point is equal to the negative gradient of electrostatic at that point E=-dv/dr
View SolutionShow that electric field intensity at any point in the electric field is equal to negative rate of change of potential with respect to distance, measured in the direction of electric intensity
View SolutionHow is electric field intensity at a point related to the potential gradient there ?
View SolutionProve that the electric field intensity at a point is equal to the negative gradient of electric potential at that point.
View SolutionIs there a point in an electric field where electric field intensity is zero but not the electric potential ?
View SolutionIs there a point in an electric field where electric potential is zero but not the electric field intensity ?
View SolutionDefine electric field intensity and electric potential.Then prove that electric field intensity is negative gradient of electric potential
View SolutionHow is electric field intensity at a point related to the potential gradient there ?
View Solution
