A rough inclined plane has its angle of inclination equal to 45∘ and μ=0.5. The magnitude of the least force in kg wt parallel to the plane required to move a body of 4 kg up the plane is
3√2
2√2
√2
1/√2
The correct Answer is:A
To solve the problem, we need to determine the least force required to move a body of mass 4 kg up a rough inclined plane with an angle of inclination of 45 degrees and a coefficient of friction (μ) of 0.5.
Step 1: Identify the forces acting on the body
When the body is on the inclined plane, the following forces act on it:
1. Weight (W) of the body acting vertically downward.
2. Normal force (N) acting perpendicular to the surface of the incline.
3. Frictional force (f) acting parallel to the incline, opposing the motion.
Step 2: Calculate the weight of the body
The weight (W) of the body can be calculated using the formula:
W=m⋅g
Where:
- m=4kg (mass of the body)
- g=9.8m/s2 (acceleration due to gravity)
Calculating the weight:
W=4kg⋅9.8m/s2=39.2N
Step 3: Resolve the weight into components
The weight can be resolved into two components:
1. Perpendicular to the incline: W⊥=W⋅cos(θ)
2. Parallel to the incline: W∥=W⋅sin(θ)
For θ=45∘:
W⊥=39.2⋅cos(45∘)=39.2⋅1√2≈27.8N
W∥=39.2⋅sin(45∘)=39.2⋅1√2≈27.8N
Step 4: Calculate the normal force
The normal force (N) is equal to the perpendicular component of the weight:
N=W⊥=27.8N
Step 5: Calculate the frictional force
The frictional force (f) can be calculated using the formula:
f=μ⋅N
Where μ=0.5:
f=0.5⋅27.8≈13.9N
Step 6: Determine the total force required to move the body up the incline
The total force (F) required to move the body up the incline must overcome both the parallel component of the weight and the frictional force:
F=W∥+f
F=27.8+13.9≈41.7N
Step 7: Convert the force into kg weight
To convert the force from Newtons to kg weight, we use the relation:
1kg wt=9.8N
Thus, the force in kg wt is:
Fkg wt=41.79.8≈4.25kg wt
Final Answer
The magnitude of the least force required to move the body of 4 kg up the plane is approximately 4.25 kg wt.
---
When the body is on the inclined plane, the following forces act on it:
1. Weight (W) of the body acting vertically downward.
2. Normal force (N) acting perpendicular to the surface of the incline.
3. Frictional force (f) acting parallel to the incline, opposing the motion.
The weight (W) of the body can be calculated using the formula:
W=m⋅g
Where:
- m=4kg (mass of the body)
- g=9.8m/s2 (acceleration due to gravity)
W=4kg⋅9.8m/s2=39.2N
The weight can be resolved into two components:
1. Perpendicular to the incline: W⊥=W⋅cos(θ)
2. Parallel to the incline: W∥=W⋅sin(θ)
W⊥=39.2⋅cos(45∘)=39.2⋅1√2≈27.8N
W∥=39.2⋅sin(45∘)=39.2⋅1√2≈27.8N
The normal force (N) is equal to the perpendicular component of the weight:
N=W⊥=27.8N
The frictional force (f) can be calculated using the formula:
f=μ⋅N
Where μ=0.5:
f=0.5⋅27.8≈13.9N
The total force (F) required to move the body up the incline must overcome both the parallel component of the weight and the frictional force:
F=W∥+f
F=27.8+13.9≈41.7N
To convert the force from Newtons to kg weight, we use the relation:
1kg wt=9.8N
Thus, the force in kg wt is:
Fkg wt=41.79.8≈4.25kg wt
The magnitude of the least force required to move the body of 4 kg up the plane is approximately 4.25 kg wt.
Similar Questions
A body of mass 2 kg is lyign on rough inclined plane of inclination 30 0 . Find the mgnitude of the force parallel to the incline needed to make tkheblock move a. up the incline b. down the incline. Coefficient of static friction =0.2
Repeat part a. of problem 6 if the push is applied horizontally and not parallel to the incline.
View SolutionA body of mass 2 kg is lyign on rough inclined plane of inclination 300. Find the mgnitude of the force parallel to the incline needed to make tkheblock move a. up the incline b. down the incline. Coefficient of static friction =0.2
View Solution
Knowledge Check
A rough inclined plane has its angle of inclination equal to 45∘ and μ=0.5. The magnitude of the least force in kg wt parallel to the plane required to move a body of 4 kg up the plane is
A3√2B2√2C√2D1/√2A body of mass m is kept on a rough fixed inclined plane of angle of inclination θ=30∘. It remains stationary. Then magnitude of force acting on the body by the inclined plane is equal to :
AmgBmgsinθCmgcosθDnone of theseA body of mass m=18kg is placed on an inclined plane the angle of inclination is α=37∘ and is attached to the top end of the slope with a thread which is parallel to the slope. Then the plane slope is moved with a horizontal acceleration of a. Friction is negligible.
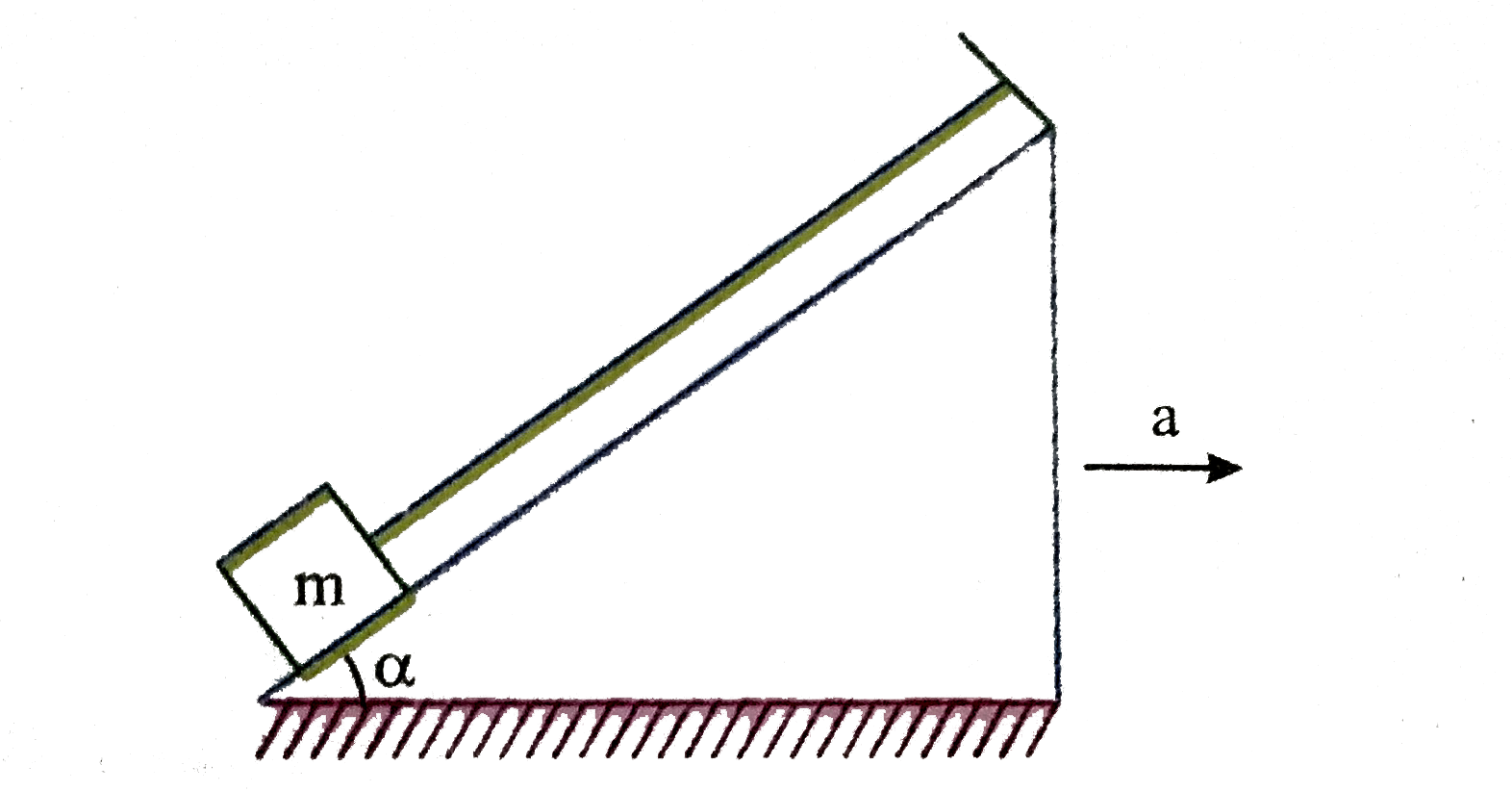
THe acceleration if the body pushes the plane with a force of 34mg is .A543m/s2B0.5m/s2C0.75m/s2D56m/s2
A mass of 100kg is resting on a rough inclined plane of angle 30∘ If the coefficient of friction is 1/√3 find the greatest and the least forces that acting parallel to the plane in both cases just maintain the mass in equilibrium .
View SolutionA block of mas M is resting on an inclined plane as shown in the figure. The inclination of the plane to the horizontal is gradually increased. It is found that when the angle of inclination is θ the block just begins to slide down the plane. What is the minimum force F applied parallel to the plane that would just make the block move up the plane ?
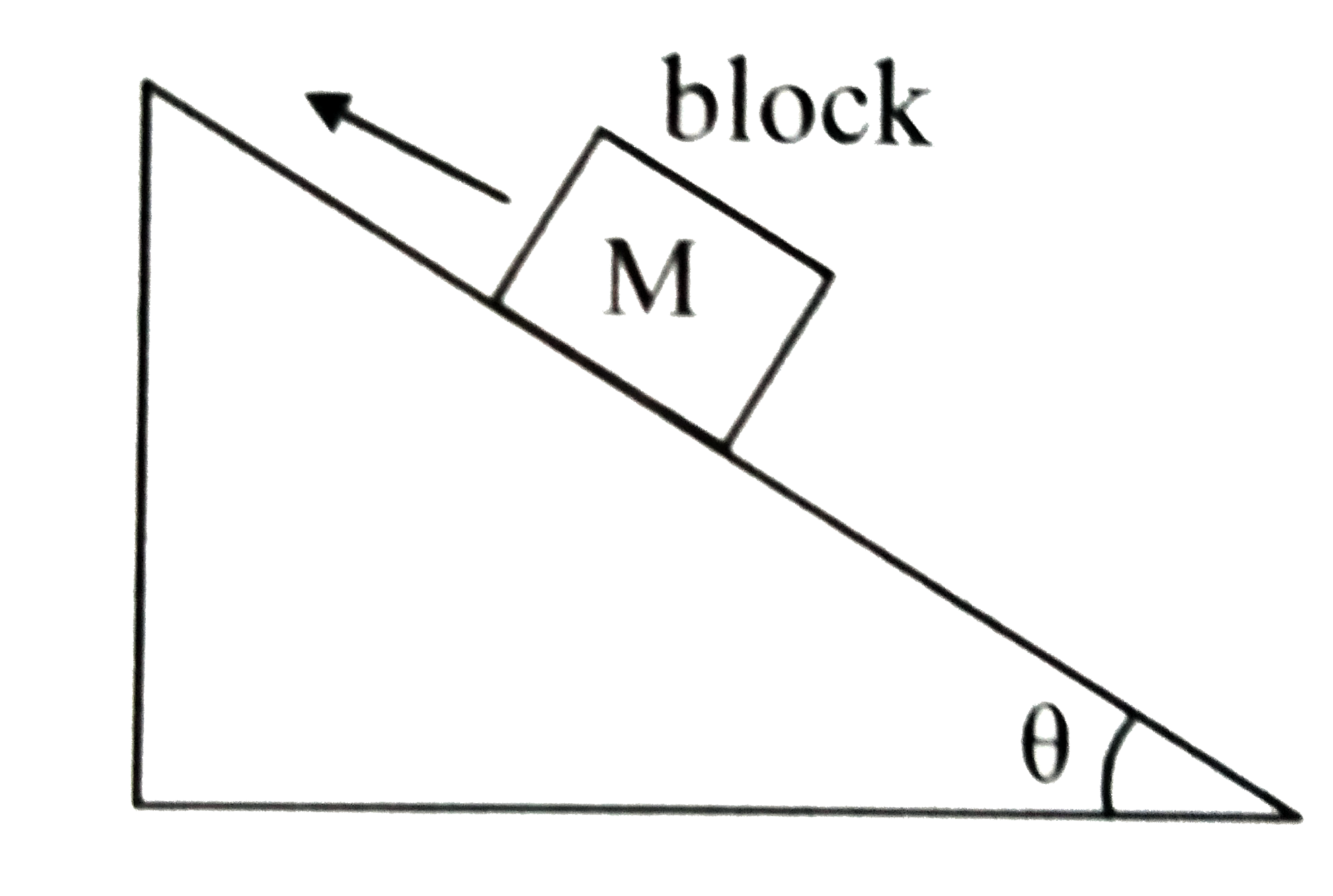
View SolutionA block of mas M is resting on an inclined plane as shown in the figure. The inclination of the plane to the horizontal is gradually increased. It is found that when the angle of inclination is θ the block just begins to slide down the plane. What is the minimum force F applied parallel to the plane that would just make the block move up the plane ?

View SolutionA body of mass 10kg is lying on a rough inclined plane of inclination 37∘ and μ=1/2 , the minimum force required to pull the body up the plane is
View SolutionThe least force required to pull a body of weight W up an inclined rough plane is
View Solution

