A ball is thrown from the top of the Qutab Minar 200 ft. high with a velocity 80 ft. per second at an elevation of above the horizon. The horizontal distance from the foot of the minar to. the point where it hits the ground is
200 ft.
The correct Answer is:B
To solve the problem of a ball thrown from the top of Qutab Minar, we will break the motion into horizontal and vertical components and use the equations of motion to find the horizontal distance traveled by the ball before it hits the ground.
1. Identify the Given Data:
- Height of Qutab Minar (h) = 200 ft
- Initial velocity (v) = 80 ft/s
- Angle of projection (θ) = 30°
- Acceleration due to gravity (g) = 32 ft/s²
2. Calculate the Vertical and Horizontal Components of the Initial Velocity:
- The vertical component (v_y) is given by:
vy=vsin(θ)=80sin(30°)=80×12=40 ft/s
- The horizontal component (v_x) is given by:
vx=vcos(θ)=80cos(30°)=80×√32=40√3 ft/s
3. Set Up the Vertical Motion Equation:
- The vertical motion can be described by the equation:
h=vyt−12gt2
- Substituting the known values:
−200=40t−12×32t2
- Rearranging gives:
16t2−40t−200=0
4. Solve the Quadratic Equation:
- Using the quadratic formula t=−b±√b2−4ac2a:
- Here, a=16, b=−40, and c=−200.
- Calculate the discriminant:
b2−4ac=(−40)2−4×16×(−200)=1600+12800=14400
- Now substituting into the quadratic formula:
t=40±√144002×16=40±12032
- This gives two possible solutions for t:
t=16032=5 seconds(valid, as time cannot be negative)
t=−8032(not valid)
5. Calculate the Horizontal Distance:
- The horizontal distance (R) can be calculated using:
R=vx⋅t=40√3⋅5=200√3 ft
Final Answer:
The horizontal distance from the foot of the Qutab Minar to the point where the ball hits the ground is 200√3 ft.
---
- Height of Qutab Minar (h) = 200 ft
- Initial velocity (v) = 80 ft/s
- Angle of projection (θ) = 30°
- Acceleration due to gravity (g) = 32 ft/s²
- The vertical component (v_y) is given by:
vy=vsin(θ)=80sin(30°)=80×12=40 ft/s
- The horizontal component (v_x) is given by:
vx=vcos(θ)=80cos(30°)=80×√32=40√3 ft/s
- The vertical motion can be described by the equation:
h=vyt−12gt2
- Substituting the known values:
−200=40t−12×32t2
- Rearranging gives:
16t2−40t−200=0
- Using the quadratic formula t=−b±√b2−4ac2a:
- Here, a=16, b=−40, and c=−200.
- Calculate the discriminant:
b2−4ac=(−40)2−4×16×(−200)=1600+12800=14400
- Now substituting into the quadratic formula:
t=40±√144002×16=40±12032
- This gives two possible solutions for t:
t=16032=5 seconds(valid, as time cannot be negative)
t=−8032(not valid)
- The horizontal distance (R) can be calculated using:
R=vx⋅t=40√3⋅5=200√3 ft
The horizontal distance from the foot of the Qutab Minar to the point where the ball hits the ground is 200√3 ft.
Similar Questions
A ball is thrown from the top of a tower of 61m high with a velocity 24.4ms−1 at an elevation of 30∘ above the horizontal. What is the distance from the foot of the tower to the point where the ball hits the ground?
View SolutionA stone is thrown up from the top of a tower 20,m with a velocity of 24m/s a tan elevation of 30∘ above the horizontal. Find the horizontal distance from the foot of the tower to the point at which the stone hits the ground. Take g=10m/s2
View Solution
Knowledge Check
A ball is thrown from the top of 36m high tower with velocity 5m/ss at an angle 37∘ above the horizontal as shown. Its horizontal distance on the ground is closest to [g=10m/s2
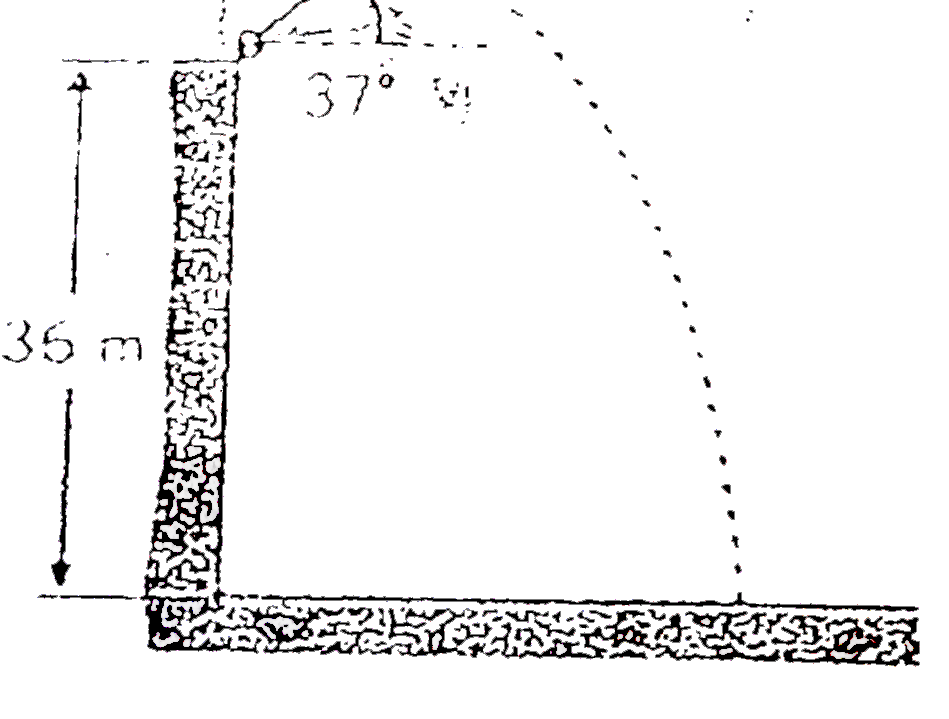 : A12mB18mC24mD30m
: A12mB18mC24mD30mA ball is thrown from the top of tower with an initial velocity of 10ms−1 at an angle of 30∘ with the horizontal. If it hits the ground of a distance of 17.3m from the back of the tower, the height of the tower is (Takeg=10ms−2)
A5mB20mC15mD10mA ball is thrown from the top of a 60m high tower with velocity 20√2m/s at 45∘ elevation of path at highest point. (g=10m/s2)
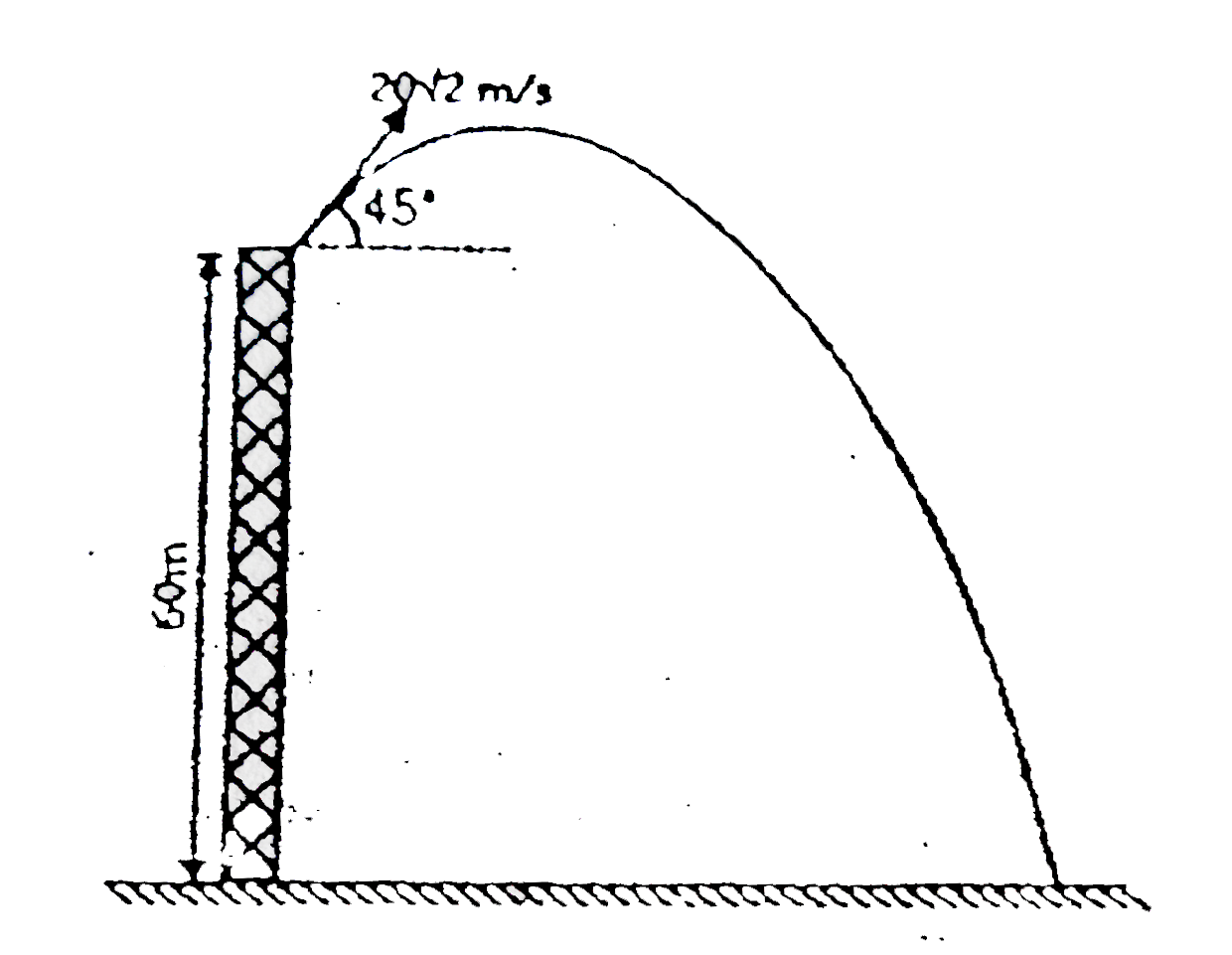 A10mB20mC40mD200m
A10mB20mC40mD200m
A ball is thrown from the top of a tower with an initial velocity of 10 m//s at an angle of 30∘above the horizontal. It hits the ground at a distance of 17.3 m from the base of the tower. The height of the tower (g=10m/s2) will be
View SolutionA ball is thrown from the top of a tower with an intial velocity of 10 m//s at an angle 37∘ above the horizontal, hits the ground at a distance 16 m from the base of tower. Calculate height of tower. [g=10m/s2]
View SolutionA stone is thrown from the top of a tower of height 50 m with a velocity of 30 m per second at an angle of 30∘ above the horizontal. Find (a) the time during which the stone will be in air, (b) the distance from the tower base to where the stone will hit the ground, (c) the speed with which the stone will hit the ground, (d) the angle formed by the trajectory of the stone with the horizontal at the point of hit.
View SolutionA ball is thrown with a velocity of 30ms−1 from the top of a building 200m high . The ball makes an angle of 30∘ with the horizontal . Calculate the distance from the foot of the building where the ball strikes the ground (g=10ms−2).
View SolutionA ball is thrown from a point in level with velocity u and at a horizontal distance r from the top of a tower of height h.
At what horizontal distance x from the foot of the tower does the ball hit the ground ?
View Solution
