In ΔABC it is given distance between the circumcentre (O) and orthocentre (H) is R√1−8cosAcosBcosC. If Q is the midopoint of OH, then AQ is Solution in Punjabi
The correct Answer is:OP=R√1−8cosBcosC
Step by step video & text solution for In Delta ABC it is given distance between the circumcentre (O) and orthocentre (H) is R sqrt(1-8 cos A cos B cos C). If Q is the midopoint of OH, then AQ is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - SOLVED EXAMPLES1videos
PROPERTIES AND SOLUTION OF TRIANGLES
- BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise For Sesssion 120videos
PROPERTIES AND SOLUTION OF TRIANGLES
- BOOK - ARIHANT MATHSCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)52videos
PRODUCT OF VECTORS
- BOOK - ARIHANT MATHSCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)38videos
SEQUENCES AND SERIES
Similar Questions
Match the statements of Column I with values of Column II.
 01:46View Solution
01:46View SolutionIn the given figure,if AB=AC,∠BAD=30∘andAE=AD, then x is equal to
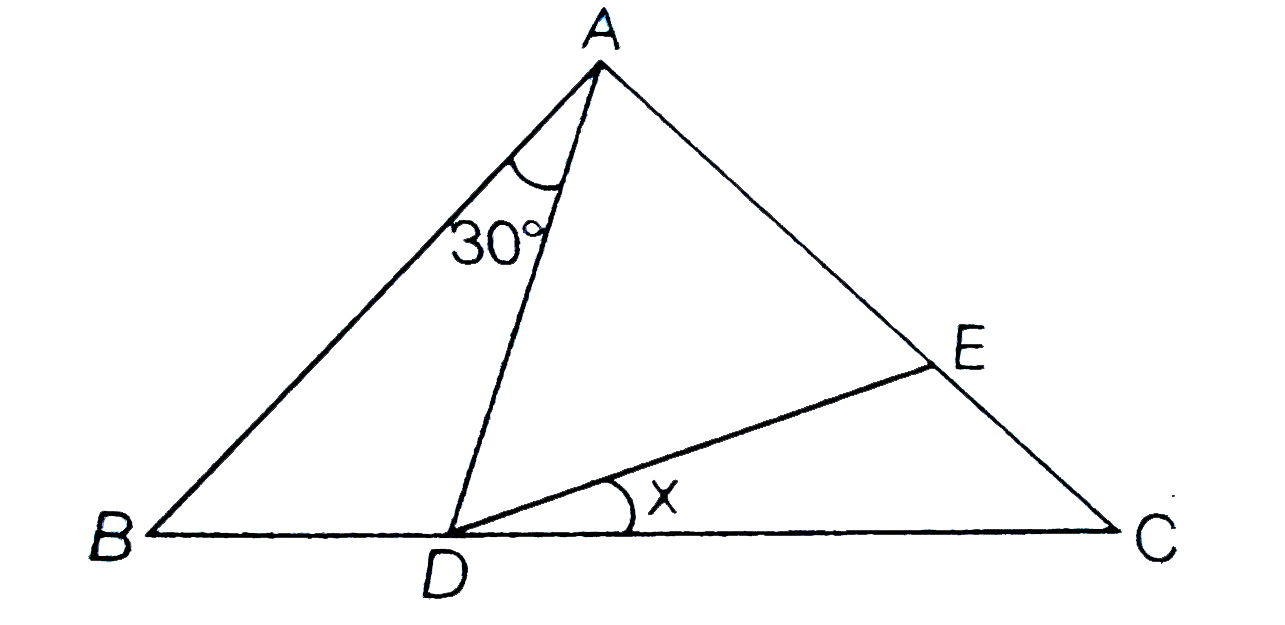 12:47View Solution
12:47View SolutionLet O be the origin and let PQR be an arbitrary triangle. The point S is such that ¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OQ+¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OP+¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OR+¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OS Then the triangle PQR has S as its
03:45View SolutionLet a,b,c be in A.P. and |a|<1,|b|<1|c|<1.ifx=1+a+a2+....to ∞,y=1+b+b2+....to ∞and,z=1+c+c2+...to ∞, then x,y,z are in
View SolutionThe orthocentre of the triangle ABC is 'B' and the circumcentre is 'S' (a, b). If A is the origin, then th co-ordinates of C are
06:54View SolutionThe distance between the circumcentre and orthocenter of a Delta ABC is R sqrt(1-lambda cos A*cos B*cos C), then lambda=
02:21View SolutionIn Delta ABC, if sin A+sin B+sin B+sin C=1+sqrt(2) and cos A+cos B+cos C=sqrt(2) then the triangle is
View SolutionProve that the distance between the circumcenter and the orthocenter of triangle ABC is R√1−8cosAcosBcosC
03:24View SolutionIn a ΔABC, show that acosA+bcosB+ccosCa+b+c=rR
02:14View SolutionIf the incircel of the triangle ABC, through it's circumcentre, then the cosA+cosB+cosC is
02:14View SolutionIf H is the orthocentre of ΔABC, then : cos(∠AHB)=
View SolutionIf in a ΔABC,B is orthocentre and if circumcentre of ΔABC is (2,4) and vertex A is (0,0) then co-ordinates of vertex 'C' is
02:16View SolutionIf in a ΔABC,B is orthocentre and if circumcentre of ΔABC is (2,4) and vertex A is (0,0) then co-ordinates of vertex C is
04:55View SolutionIf the line joining the circumcentre 'O' and the incentre I is parallel to BC, then cosB+cosC =
09:45View SolutionA: In a ΔABC, if A,B,C are in A.P. and triangle is equilateral cos A+2 cos B+ cos C=2
R: In a ΔABC, if A,B,C are in A.P. and cos A+ cos B+ cos C=2 then the triangle is isosceles.02:27View SolutionCo-ordinates of the vertices of a triangle are (2, 0), (6, 0) and (1, 5). The distance between circumcentre and orthocentre is :
07:53View Solution
