Question

In a parallelogram OABC vectors a,b,c respectively, THE POSITION VECTORS OF VERTICES A,B,C with reference to O as origin. A point E is taken on the side BC which divides it in the ratio of 2:1 also, the line segment AE intersects the line bisecting the angle ${\displaystyle \angle AOC}$ internally at point P. if CP when extended meets AB in points F, then
Q. The position vector of point P is

Options

A. `(2|a|)/(||a|-3|c||)`
B. `(|a|)/(||a|-3|c||)`
C. `(3|a|)/(||a|-3|c||)`
D. `(3|c|)/(3||c|-|a||)`

Answer

B

Explanation

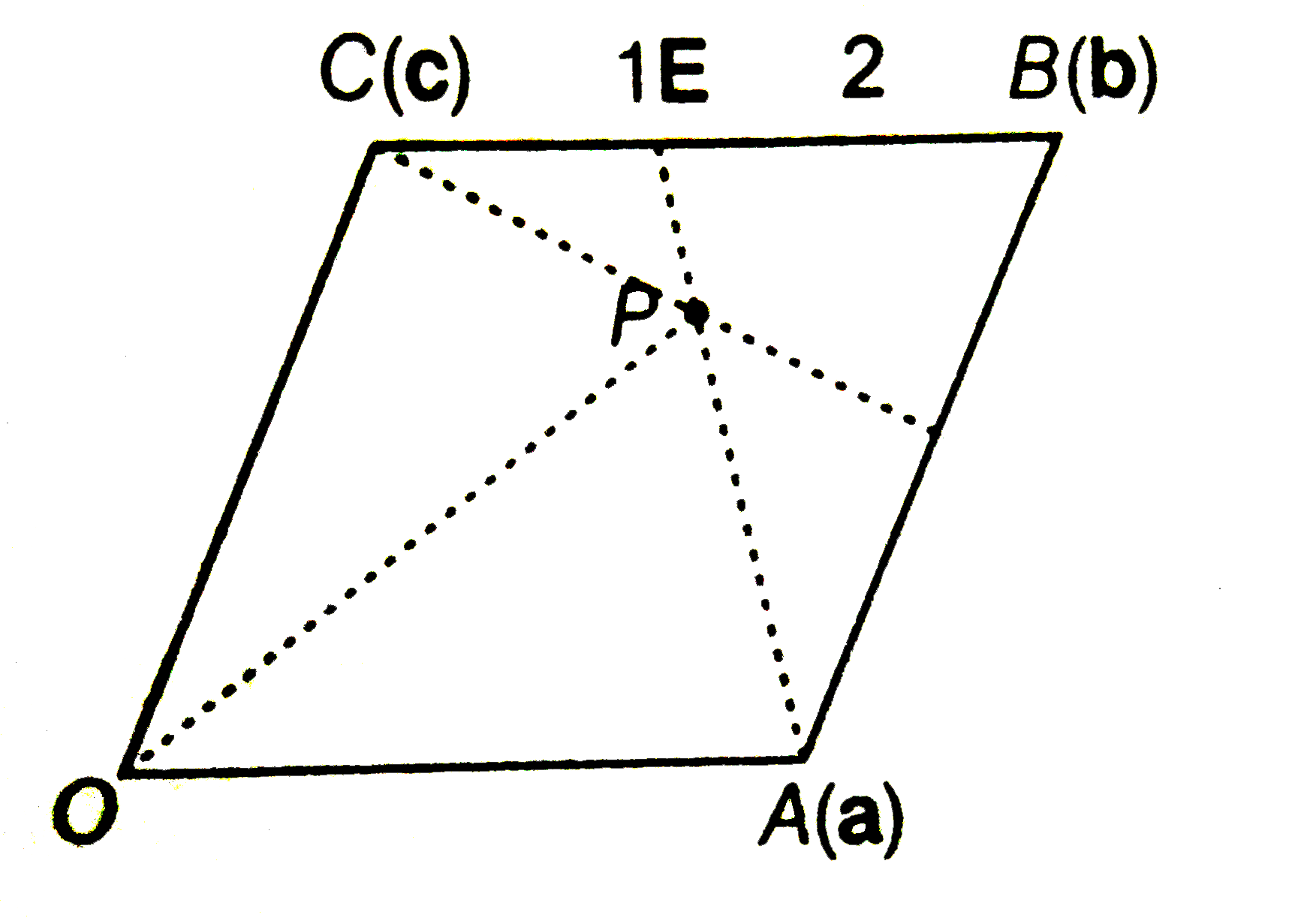
let the position vector fo A and C be a and c respectively.
therefore,
Position vector of
`B=b=a+c` . . (i)
Also, position vector of
`E=(b+2c)/(3)=(a+3c)/(3)` . . . (ii)
Now, point P lies on angle bisector off `angleAOC`. thus,
Position vector of point
`P=lamda((a)/(|a|)+(b)/(|b|))` . . (iii)
Also, let P divides EA in ration `mu:1`. therefore, position vector of P
`=(mua+(a+3c)/(3))/(mu+1)=((3mu+1)a+3c)/(3(mu+1))` . . . (iv)
Comparing eqs. (iii) and (iv), we get
`lamda((a)/(|a|)+(c)/(|c|))=((3mu+1)a+3c)/(3(mu+1))`
`implies(lamda)/(|a|)=(3mu+1)/(3(mu+1)) and (lamda)/(|c|)=(1)/(mu+1)`
`implies(3|c|-|a|)/(3|a|)=mu`
`implies(lamda)/(|c|)=(1)/((3|c|-|a|)/(3|a|)+1)implies lamda=(3|a||c||)/(3|c|+2|a|)`
Let F divides AB in ratio t:1, then position vector of F is
`(tb+a)/(t+1)`
Now, points C, P,F are collinear, then, CF=mCP
`implies(t(a+c))/(t+1)-c=m{(3|a||c|)/(3|c|+2|a|)((a)/(|a|)+(c)/(|c|))-c}`
Comparing coefficient, we get
`(t)/(t+1)=m(3|c|)/(3|c|+2|a|)`
and `(-1)/(t+1)=m(|a|-3|c|)/(3|c|+2|a|)`
`t=(3|c|)/(3|c|-|a|)`