ABCD is a parallelogram. L is a point on BC which divides BC in the ratio 1:2. AL intersects BD at P.M is a point on DC which divides DC in the ratio 1:2 and AM intersects BD in Q.
PQ:DB is equal to Solution in Punjabi
23
13
12
34
The correct Answer is:B
∴PQ=12DB,
i.e., PQ:DB=1:2
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise For Session 17videos
VECTOR ALGEBRA
- BOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise For Session 217videos
VECTOR ALGEBRA
- BOOK - ARIHANT MATHSCHAPTER - TRIGONOMETRIC FUNCTIONS AND IDENTITIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)18videos
TRIGONOMETRIC FUNCTIONS AND IDENTITIES
Similar Questions
Classify the following measure as scalar and vector: 10Kg
03:36View SolutionIf a=2ˆi−ˆj+2ˆkandb=−ˆi+ˆj−ˆk, then find a+b. Also, find a unit vector along a+b.
06:28View SolutionLet αandβ be non-zero real numbers such that 2(cosβ−cosα)+cosαcosβ=1. Then which of the following is/are true ?
03:44View SolutionABCD is a parallelogram. L is a point on BC which divides BC in the ratio 1:2. AL intersects BD at P.M is a point on DC which divides DC in the ratio 1:2 and AM intersects BD in Q.
Point P divides AL in the ratioView SolutionABCD is a parallelogram. L is a point on BC which divides BC in the ratio 1:2. AL intersects BD at P.M is a point on DC which divides DC in the ratio 1:2 and AM intersects BD in Q.
Point Q divides DB in the ratio04:20View SolutionIn a quadrilateral ABCD, the point P divides DC in the ratio 1:2 and Q is the mid-point of AC. If AB+2AD+BC-2 DC=k PQ, then k is equal to
05:27View SolutionIn a quadrilateral ABCD, the point P divides DC in the ratio 1:2 and Q is the mid-point of AC. If AB+2AD+BC-2 DC=k PQ, then k is equal to
04:08View SolutionABCD is a parallelogram. L is a point on BC which divides BC in the ratio 1:2. AL intersects BD at P. M is a point on DC which divides DC in the ratio 1:2 and AM intersects BD in Q.
Point P divides AL in the ratio -View SolutionABCD is a parallelogram. L is a point on BC which divides BC in the ratio 1:2. AL intersects BD at P. M is a point on DC which divides DC in the ratio 1:2 and AM intersects BD in Q.
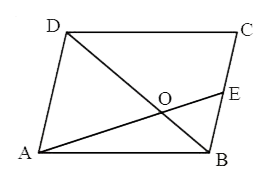
Point Q divides DB in the ratio -05:15View SolutionIn the given figure, ABCD is a parallelogram. AE divides the line segment BD in the ratio 1 : 2. If BE = 1.5 cm find BC.
 View Solution
View SolutionIn a quadrilateral ABCD, the point P divides DC in the ratio 1:2 and Q is the mid point of AC. If −−→AB+2−−→AD+−−→BC−2−−→DC=k−−→PQ then k is equal to
View SolutionABCD একটি সামান্তরিক |L, BC বাহুকে 1:2 অনুপাতে বিভক্ত করে | AL, BD-কে P বিন্দুতে ছেদ করে | M একটি বিন্দু যা DC-কে 1:2 অনুপাতে বিভক্ত করে এবং AM, BD-কে Q বিন্দুতে ছেদ করে | P বিন্দু AL-কে যে অনুপাতে বিভক্ত করে তার মান -
05:30View SolutionABCD একটি সামান্তরিক |L, BC বাহুকে 1:2 অনুপাতে বিভক্ত করে | AL, BD-কে P বিন্দুতে সমদ্বিখণ্ডিত করে | M একটি বিন্দু যা DC-কে 1:2 অনুপাতে বিভক্ত করে এবং AM, BD-কে Q বিন্দুতে ছেদ করে | Q বিন্দু যে অনুপাতে DB-কে বিভক্ত করে-
04:53View SolutionABCD একটি সামান্তরিক |L, BC বাহুকে 1:2 অনুপাতে বিভক্ত করে | AL, BD-কে P বিন্দুতে সমদ্বিখণ্ডিত করে | M একটি বিন্দু যা DC-কে 1:2 অনুপাতে বিভক্ত করে এবং AM, BD-কে Q বিন্দুতে ছেদ করে | PQ:QB =
04:23View SolutionABCD is a parallelogram. L is a point on BC which divides BC in the ratio 1:2. AL intersects BD at P. M is a point on DC which divides DC in the ratio 1:2 and AM intersects BD in Q.
Point P divides AL in the ratio05:39View SolutionABCD is a parallelogram. L is a point on BC which divides BC in the ratio 1:2. AL intersects BD at P.M is a point on DC which divides DC in the ratio 1:2 and AM intersects BD in Q.
Point Q divides DB in the ratioView Solution
