Let position vectors of point A,B and C of triangle ABC represents be $ˆ i + ˆ j + 2 ˆ k, ˆ i + 2 ˆ j + ˆ k$ and $2 ˆ i + ˆ j + ˆ k$ . Let $l_{1}, l_{2}$ and $l_{3}$ be the length of perpendicular drawn from the orthocenter 'O' on the sides AB, BC and CA, then $(l_{1} + l_{2} + l_{3})$ equalsSolution in Punjabi

A

$\frac{2}{\sqrt{6}}$

B

$\frac{3}{\sqrt{6}}$

C

$\frac{\sqrt{6}}{2}$

D

$\frac{\sqrt{6}}{3}$ .

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

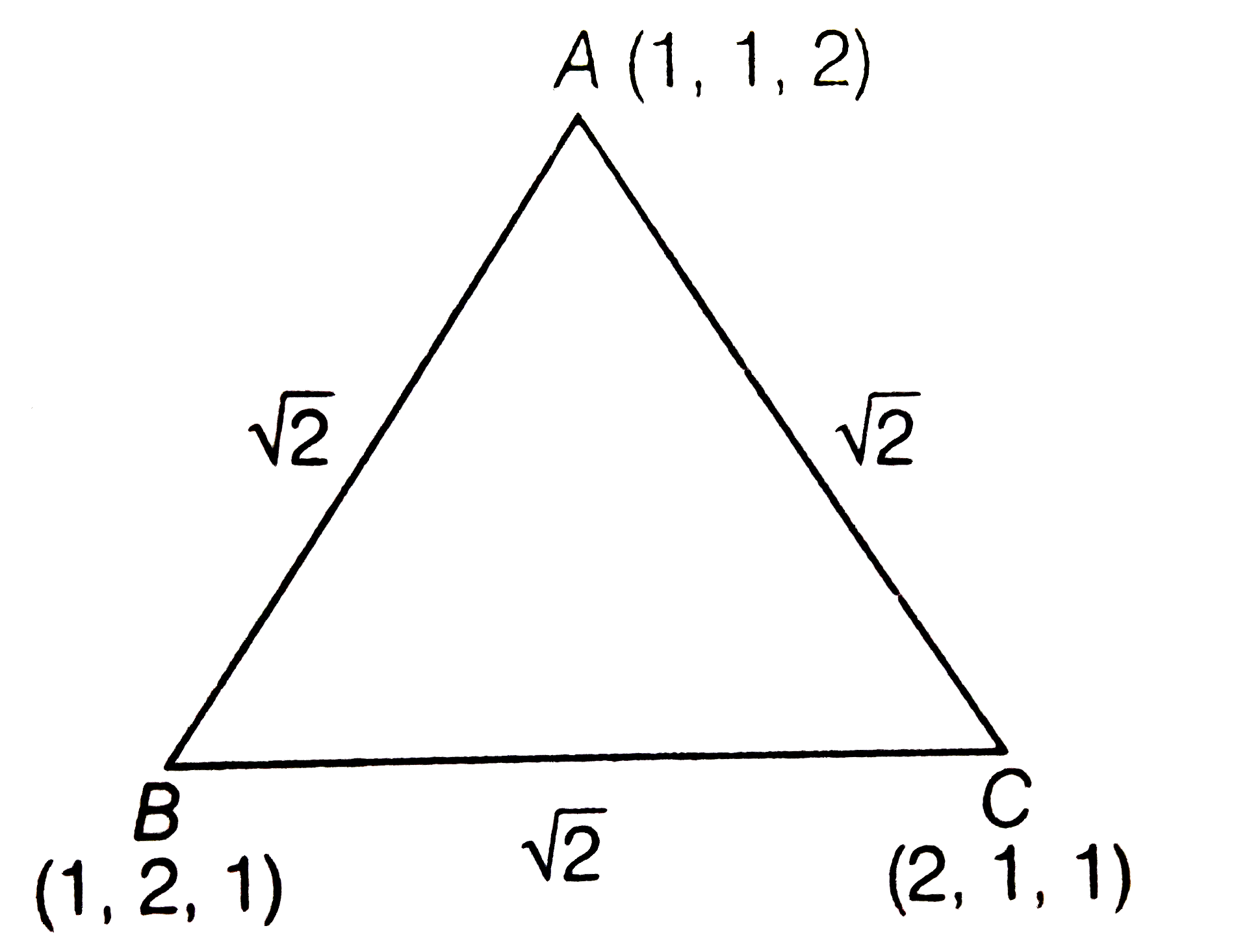
Clearly, triangle formed by the given points $ˆ i + ˆ j + 2 ˆ k$ ,
$ˆ i + 2 ˆ j + ˆ k and 2 ˆ i + ˆ j + ˆ k$ is equilateral as $A B = B C = A C = \sqrt{2}$ .
$∴$ Distance of orthocentre 'O' from the sides is equal to inradius of the triangle.
$∴ l_{1} = l_{2} = l_{3} =$ inradius $= r = \frac{Δ}{s} = \frac{\frac{\sqrt{3}}{4} {(\sqrt{2})}^{2}}{\frac{3}{2} (\sqrt{2})} = \frac{1}{\sqrt{6}}$
$\Rightarrow (l_{1} + l_{2} + l_{3}) = \frac{3}{\sqrt{6}} = \frac{\sqrt{6}}{2}$

Updated on:21/07/2023

|

Class 12 MATHS VECTOR ALGEBRA

Topper's Solved these Questions

Similar Questions

ARIHANT MATHS-VECTOR ALGEBRA-Exercise (Questions Asked In Previous 13 Years Exam)

Home
Ask Doubt
Profile