Which of the following cannot have a proper subset ?
{x:x∈Q,5<x<7}
{x:x∈Z,−4<x<4}
{x:∈N,5<x<6}
{x:x+1=0,x∈Z}
The correct Answer is:C
To solve the question "Which of the following cannot have a proper subset?", we will analyze each option step by step:
Step 1: Understand Proper Subsets
A proper subset of a set is a subset that contains some but not all elements of the original set. A set that has only one element cannot have a proper subset because the only subset it can have is itself.
Step 2: Analyze Each Option
Option A:
- Set: x such that x∈Q and 5<x<7.
- The numbers between 5 and 7 are rational numbers like 5.1, 5.2, ..., 6.9.
- This set contains infinitely many elements (rational numbers), so it can have proper subsets.
Option B:
- Set: x such that x∈Z and −4<x<4.
- The integers in this range are -3, -2, -1, 0, 1, 2, 3.
- This set has several elements, so it can have proper subsets.
Option C:
- Set: x such that x∈N and 5<x<6.
- The only natural number that satisfies this condition is none, as natural numbers are whole numbers starting from 1 and do not include decimals.
- Therefore, this set is empty. An empty set has no elements, and thus cannot have a proper subset.
Option D:
- Set: x such that x+1=0 where x∈Z.
- The solution to this equation is x=−1.
- This set contains only one element (-1), which means it cannot have a proper subset.
Conclusion:
The only option that cannot have a proper subset is Option C, as it is an empty set.
Final Answer:
Option C cannot have a proper subset.
---
A proper subset of a set is a subset that contains some but not all elements of the original set. A set that has only one element cannot have a proper subset because the only subset it can have is itself.
- Set: x such that x∈Q and 5<x<7.
- The numbers between 5 and 7 are rational numbers like 5.1, 5.2, ..., 6.9.
- This set contains infinitely many elements (rational numbers), so it can have proper subsets.
- Set: x such that x∈Z and −4<x<4.
- The integers in this range are -3, -2, -1, 0, 1, 2, 3.
- This set has several elements, so it can have proper subsets.
- Set: x such that x∈N and 5<x<6.
- The only natural number that satisfies this condition is none, as natural numbers are whole numbers starting from 1 and do not include decimals.
- Therefore, this set is empty. An empty set has no elements, and thus cannot have a proper subset.
- Set: x such that x+1=0 where x∈Z.
- The solution to this equation is x=−1.
- This set contains only one element (-1), which means it cannot have a proper subset.
The only option that cannot have a proper subset is Option C, as it is an empty set.
Option C cannot have a proper subset.
Topper's Solved these Questions
- SETSBook:S CHAND IIT JEE FOUNDATIONChapter:SETSExercise:Question Bank
Explore 24 Videos
- RATIO AND PROPORTION Book:S CHAND IIT JEE FOUNDATIONChapter:RATIO AND PROPORTION Exercise:SELF ASSESSMENT SHEET - 15
Explore 10 Videos
- SIMPLE INTEREST Book:S CHAND IIT JEE FOUNDATIONChapter:SIMPLE INTEREST Exercise:Self Assessment Sheet
Explore 10 Videos
Similar Questions
Knowledge Check
Which of the following cannot clot?
ALymph onlyBPlasma onlyCSerum onlyDLymph and serumWhich of the following cannot be a base?
A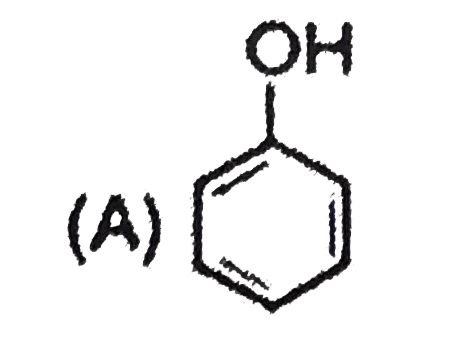 BCH3−C∣∣O−NH2C
BCH3−C∣∣O−NH2C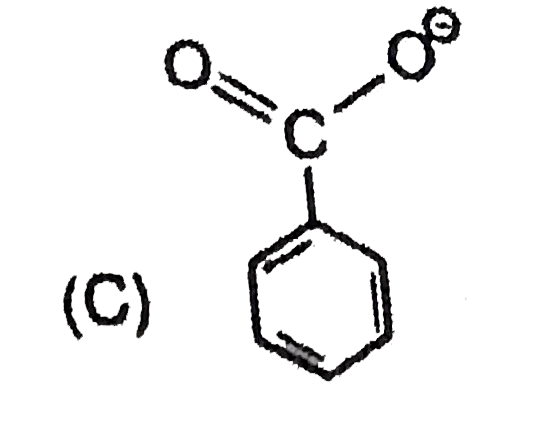 D
D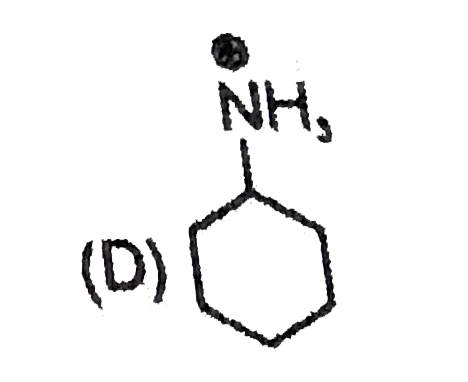
Which of the following cannot be polarized
Aradio waveBX-rayCsound wave in airDintrared radiation
