This frequency table shows the results of a small class quiz . If a student is selected at random, the probability that he or she scored 2, 4, or 5 is
Marks Frequency 1 4 2 3 3 2 4 6 5 5
320
14
710
920
The correct Answer is:C
To find the probability that a randomly selected student scored 2, 4, or 5 marks, we will follow these steps:
Step 1: Calculate the total number of students
We need to sum the frequencies of all scores given in the frequency table.
- Frequency of students who scored 1: 4
- Frequency of students who scored 2: 3
- Frequency of students who scored 3: 2
- Frequency of students who scored 4: 6
- Frequency of students who scored 5: 5
Total number of students = 4 + 3 + 2 + 6 + 5
Calculation:
- 4 + 3 = 7
- 7 + 2 = 9
- 9 + 6 = 15
- 15 + 5 = 20
Total number of students = 20
Step 2: Calculate the number of favorable outcomes
Next, we need to find out how many students scored either 2, 4, or 5 marks.
- Students who scored 2: 3
- Students who scored 4: 6
- Students who scored 5: 5
Total number of students who scored 2, 4, or 5 = 3 + 6 + 5
Calculation:
- 3 + 6 = 9
- 9 + 5 = 14
Total number of favorable outcomes = 14
Step 3: Calculate the probability
The probability P that a student scored 2, 4, or 5 is given by the formula:
P(scoring 2, 4, or 5)=Number of favorable outcomesTotal number of students
Substituting the values we found:
P(scoring 2, 4, or 5)=1420
Step 4: Simplify the fraction
Now we simplify the fraction 1420.
Both the numerator and the denominator can be divided by 2:
14÷220÷2=710
Final Answer
The probability that a randomly selected student scored 2, 4, or 5 is 710.
---
We need to sum the frequencies of all scores given in the frequency table.
- Frequency of students who scored 2: 3
- Frequency of students who scored 3: 2
- Frequency of students who scored 4: 6
- Frequency of students who scored 5: 5
- 4 + 3 = 7
- 7 + 2 = 9
- 9 + 6 = 15
- 15 + 5 = 20
Next, we need to find out how many students scored either 2, 4, or 5 marks.
- Students who scored 4: 6
- Students who scored 5: 5
- 3 + 6 = 9
- 9 + 5 = 14
The probability P that a student scored 2, 4, or 5 is given by the formula:
Now we simplify the fraction 1420.
The probability that a randomly selected student scored 2, 4, or 5 is 710.
Topper's Solved these Questions
- DATA HANDLING BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - DATA HANDLING EXERCISE - Self Assessment Sheet - 24
10 Videos
- DATA HANDLING BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - DATA HANDLING EXERCISE - Question Bank - 24 (a)
20 Videos
- CIRCUMFERENCE AND AREA OF A CIRCLE BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - CIRCUMFERENCE AND AREA OF A CIRCLE EXERCISE - SELF ASSESSMENT SHEET - 22
10 Videos
- DECIMALS BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - DECIMALS EXERCISE - SELF ASSESSMENT SHEET
10 Videos
Similar Questions
The given table shows the marks obtained by 80 students in a class test with maximum marks 100. A student of the class is selected at random. Find the probability that he gets less than 15% marks.
View SolutionThe table given below shows the marks obtained by 50 students of a class in a test with maximum marks 100.
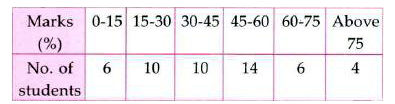
A student of the class is selected at random. Find the probability that the selected student gets
60% or more marks
View Solution
Knowledge Check
In a class, there are 10 boys and 8 girls. When 3 students are selected at random, the probability that 2 girls and 1 boy are selected, is
A35102B15102C55102D25102In a class, there are 10 boys and 8 girls. When 3 students are selected at random, the probability that 2 girls and 1 boy are selected, is
A35102B15102C55102D25102The given table shows the marks obtained by 80 students in a class test with maximum marks 100.
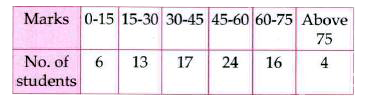
A student of the class is selected at random. Find the probability that he/she gets less than 15% marks.A1/4B3/40C9/20Dnone of these
The table given below shows the marks obtained by 50 students of a class in a test with maximum 2. marks 100.
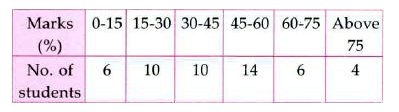
A student of the class is selected at random. Find the probability that the selected student gets
less than 15% marks
View SolutionIn a class, 30% of the students offered English, 20% offered Hindi and 10% offered both. If a student is selected at random, what is the probability that he has offered English or Hindi? 25 (b) 35 (c) 34 (d) 310 (e) None of these
View SolutionThe SD of scores 1,2,3,4,5 is-
View SolutionThe standard deviation of 5 scores 1, 2, 3, 4, 5 is
View SolutionThe probability that number selected at random from that number 1, 2, 3, 4, 5, 6, 7, 8, …., 100 is prime is
View Solution
