The tangent at a point P(acosφ,bsinφ) of the ellipse x2a2+y2b2=1 meets its auxiliary circle at two points, the chord joining which subtends a right angle at the center. Find the eccentricity of the ellipse.Solution in Bengali
The equation of the auxliary circle is x2+y2=a2 (1)
Therefore, the equation of tangent to ellipse at a point P(acosϕ,bsinϕ) is
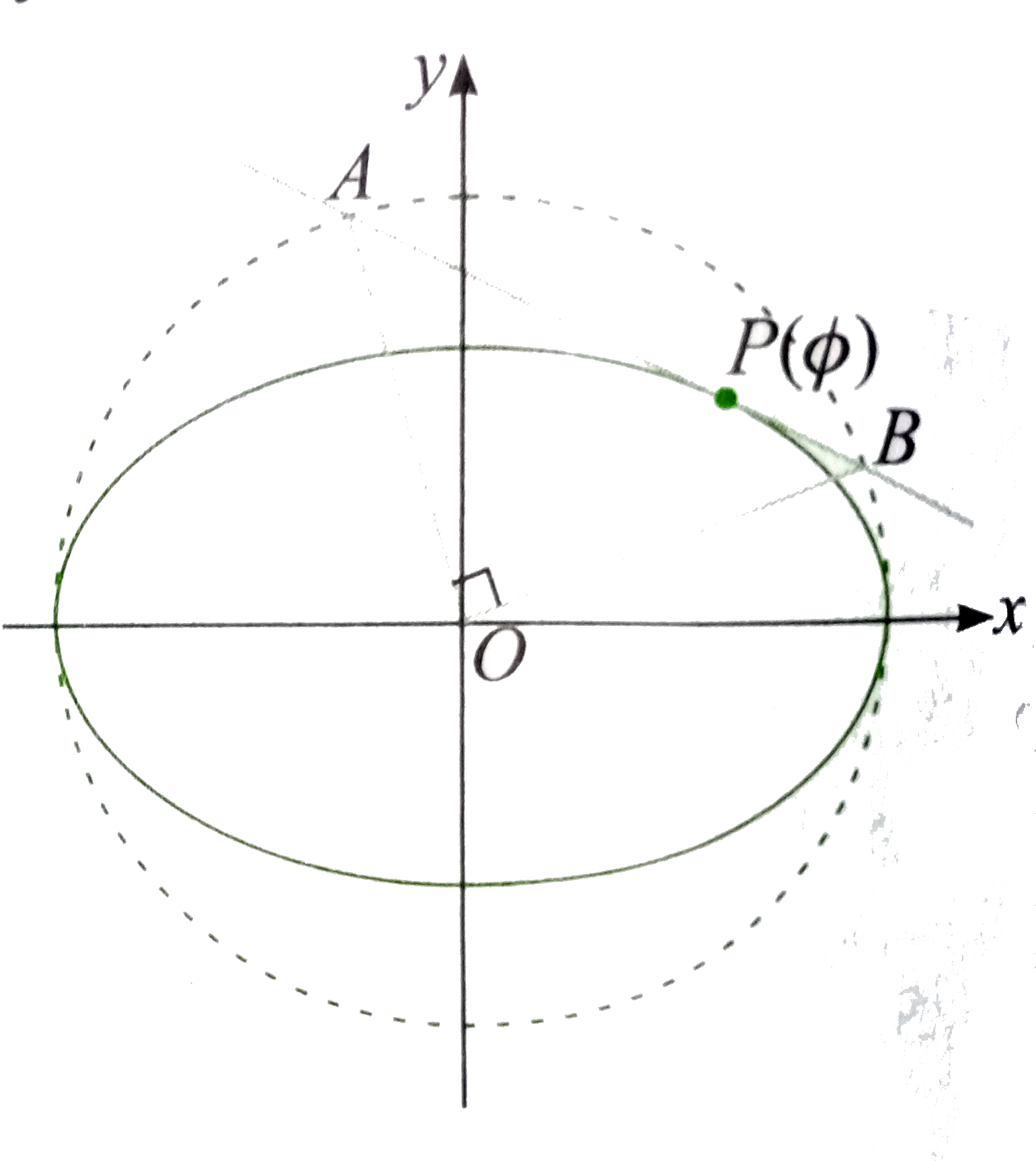
(xa)cosϕ+(yb)sinϕ=1(2)
Which meets the auxiliary circle at points A and B
Therefore, the equation of the pair of lines OA and OB is obtained by making (1) homogeneous with the help of (2). Then,
x2+y2=a2(xacosϕ+ybsinϕ)2
But ∠AOB=90∘. Therefore,
Cofficient of x2 + Coefficient of y2=0
or 1−cos2ϕ+1−a2b2sin2ϕ=0
or sin2ϕ(1−a2b2)+1=0
or(a−2−b2)sin2ϕ=b2
ora2e2sin2ϕ=a2(1−e2)
or (1+sin2ϕ)e2=1
or e=1√1+sin2ϕ
Similar Questions
If the tangent at θ on the ellipse x2a2+y2b2=1 meets the auxiliary circle at two points which subtend a right angle at the centre,then e2(2−cos2θ)=
View SolutionThe tangent at a point P(acosφ,bsinφ) of the ellipse x2a2+y2b2=1 meets its auxiliary circle at two points, the chord joining which subtends a right angle at the center. Find the eccentricity of the ellipse.
View SolutionThe tangent at a point P(acosθ,bsinθ) on the ellipse x2a2+y2b2=1 meets the auxillary circle in two points. The chord joining them subtends a right angle at the centre. Find the eccentricity of the ellipse:
View SolutionEllipse (x^(2))/(14)=(y^(2))/(5)=1 The tangent to the circle intersects the circle at two points P and Q. If the chord connecting P and B forms a right angle at the center, the ellipse of the ellipse will be
View SolutionFind the locus of middle points of chords of the ellipse x2a2+y2b2=1 which subtend right angles at its centre.
View SolutionThe tangent at a point P(acosφ,bsinφ) of the ellipse x2a2+y2b2=1 meets its auxiliary circle at two points, the chord joining which subtends a right angle at the center. Find the eccentricity of the ellipse.
View SolutionFind the range of eccentricity of the ellipse x2a2+y2b2=1, (where a > b) such that the line segment joining the foci does not subtend a right angle at any point on the ellipse.
View SolutionFind the range of eccentricity of the ellipse x2a2+y2b2=1, (where a > b) such that the line segment joining the foci does not subtend a right angle at any point on the ellipse.
View Solution
