Let C1 and C2 be two circles whose equations are x2+y2−2x=0 and x2+y2+2x=0 and P(λ,λ) is a variable point . List 1 a) P lies inside C1 but outside C2 2)P lies inside C2 but outside C1 c)P lies outside C1 but outside C2 d)P does not lie inside C2 List 2 p)λ ϵ (−∞,−1)∪(0,∞) q)λ ϵ (−∞,−1)∪(1,∞) r)λ ϵ (−1,0) s)λ ϵ (0,1) Solution in Bengali
r,s,p,q
p,s,q,r
q,p,s,r
s,r,q,p
The correct Answer is:4
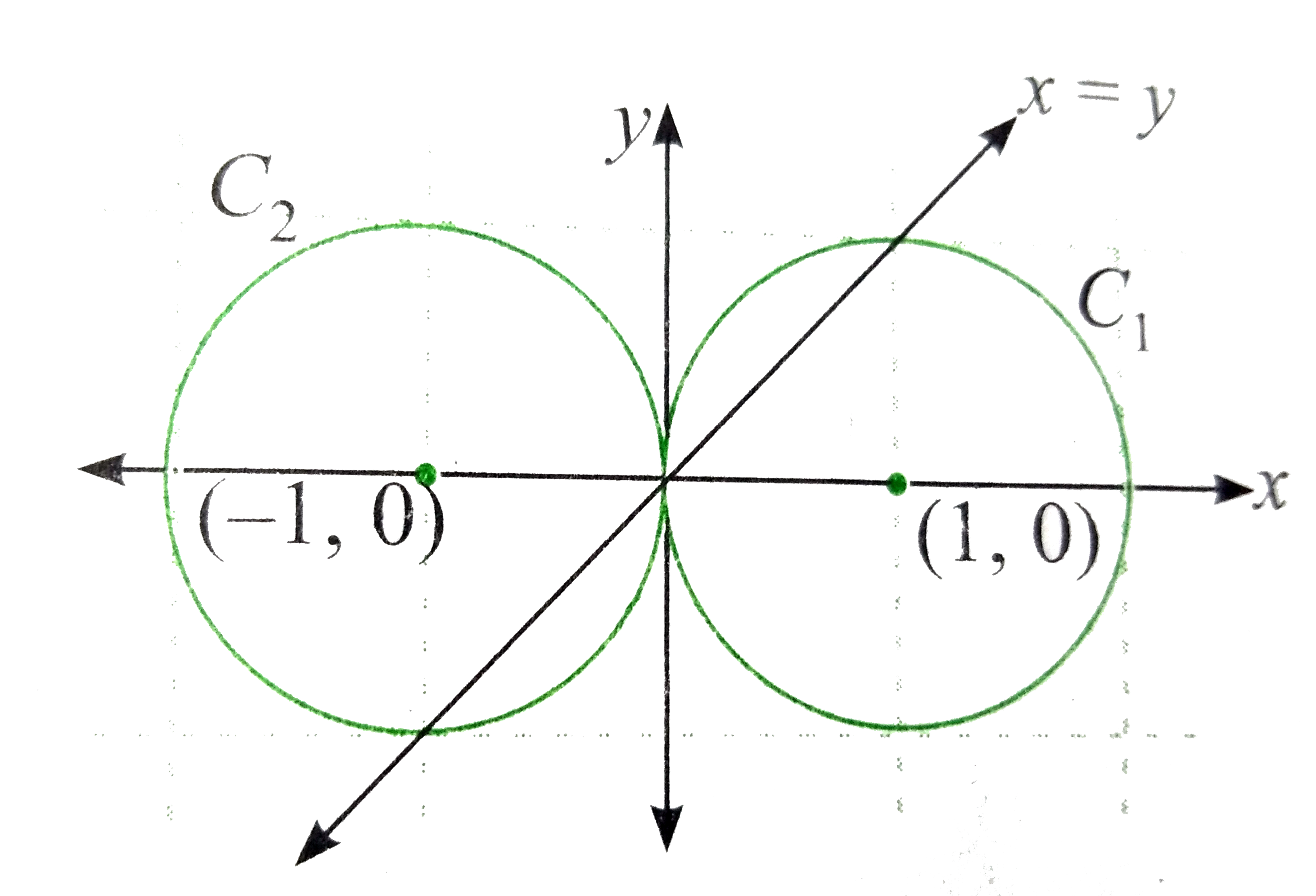
(λ,λ) lies on the line y=x ltbr> From the diagram, answer is (4)
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - NUMERICAL VALUE TYPE21videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - ARCHIVES (JEE MAIN)1videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - For Problems43videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension11videos
BINOMIAL THEOREM
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type8videos
CIRCLES
Similar Questions
Let the lines (y−2)=m1(x−5) and (y+4)=m2(x−3) intersect at right angles at P (where m1andm2 are parameters). If the locus of P is x2+y2+gx+fy+7=0 , then the value of |f+g| is__________
05:53View SolutionIf P and Q are the points of intersection of the circles x2+y2+3x+7y+2p=0 and x2+y2+2x+2y−p2=0 then there is a circle passing through P,Q and (1,1) for
05:54View SolutionTangents PA and PB are drawn to the circle (x−4)2+(y−5)2=4 from the point P on the curvey=sinx , where A and B lie on the circle. Consider the function y=f(x) represented by the locus of the center of the circumcircle of triangle PAB. Then answer the following questions.
Which of the following is true ?09:32View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is03:12View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Coordinate of Q is12:02View SolutionConsider two curves C1:y^2=4x; C2=x^2+y^2-6x+1=0. Then, a. C1 and C2 touch each other at one point b. C1 and C2 touch each other exactly at two point c. C1 and C2 intersect(but do not touch) at exactly two point d. C1 and C2 neither intersect nor touch each other
04:36View SolutionThe centres of two circles C1 and C2 each of unit radius are at a distance of 6 units from each other. Let P be the mid point of the line segment joining the centres of C1 and C2 and C be a circle touching circles C1 and C2 externally. If a common tangent to C1 and C passing through P is also a common tangent to C2 and C, then the radius of the circle C is
07:25View SolutionDelta[[ Prove that ,, 11,1,1nC1,(n+1)C1,(n+2)C1(n+1)C2,(n+2)C2,(n+3)C2]]=1
05:12View SolutionLet conditions C1 and C2 be defined as follows: C1: b^2- 4ac > 0, C2: a, -b, c are of same sign. The roots of ax^2+ bx + c = 0 are real and positive, if (a) both C1 and C2 are satisfied (b) only C2 is satisfied (c) only C1 is satisfied (d) None of these
03:30View SolutionC1 and C2 are two concentric circles, the radius of C2 being twice that of C1. From a point P on C2, tangents PA and PB are drawn to C1. Then the centroid of the triangle PAB (a) lies on C1 (b) lies outside C1 (c) lies inside C1 (d) may lie inside or outside C1 but never on C1
07:05View SolutionIf the point (3,4) lies inside and the point (−3,−4) lies outside the circle x2+y2−7x+5y−p=0, then the set of all possible values of p is
02:45View SolutionLet C1 and C2 be two circles whose equations are x2+y2−2x=0 and x2+y2+2x=0 and P(λ,λ) is a variable point . List 1 a) P lies inside C1 but outside C2 2)P lies inside C2 but outside C1 c)P lies outside C1 but outside C2 d)P does not lie inside C2 List 2 p)λ ϵ (−∞,−1)∪(0,∞) q)λ ϵ (−∞,−1)∪(1,∞) r)λ ϵ (−1,0) s)λ ϵ (0,1)
03:22View SolutionC1 and C2 are two concentric circles, the radius of C2 being twice that of C1. From a point P on C2, tangents PA and PB are drawn to C1. Then the centroid of the triangle PAB (a) lies on C1 (b) lies outside C1 (c) lies inside C1 (d) may lie inside or outside C1 but never on C1
04:49View SolutionConsider two curves C1:y2=4x ; C2=x2+y2−6x+1=0. Then, a. C1 and C2 touch each other at one point b. C1 and C2 touch each other exactly at two point c. C1 and C2 intersect(but do not touch) at exactly two point d. C1 and C2 neither intersect nor touch each other
03:58View SolutionLet E be the ellipse x29+y24=1 and C be the circle x2+y2=9 . Let PandQ be the points (1, 2) and (2, 1), respectively. Then Q lies inside C but outside E Q lies outside both CandE P lies inside both C and E P lies inside C but outside E
08:31View SolutionC1 and C2 are two concentric circles, the radius of C2 being twice that of C1. From a point P on C2, tangents PA and PB are drawn to C1. Then the centroid of the triangle PAB (a) lies on C1 (b) lies outside C1 (c) lies inside C1 (d) may lie inside or outside C1 but never on C1
03:08View Solution