The area of the region described by A={(x,y):x2+y2≤1andy2≤1−x} isSolution in Bengali
π2+43
π2−43
π2−23
π2+23
The correct Answer is:D
x2+y2≤1 represents the rgeion inside the circle x2+y2=1.
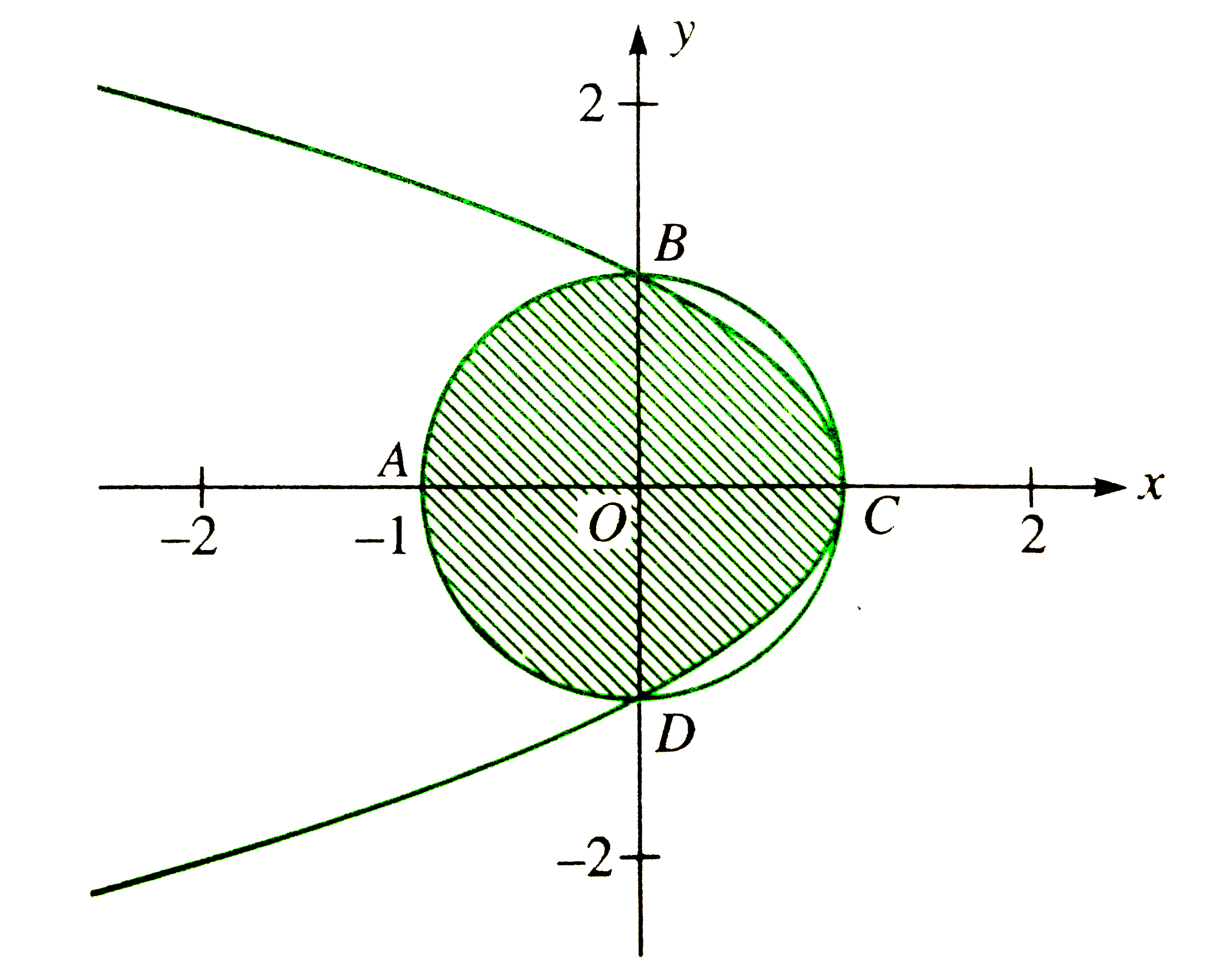
y2≤1−x, represents the region inside parabola y2=1−x towards focus.
The common region is as shown in the figure.
The area of shaded region
= Area of semicircle ADOBA+ Area of region ODCBO
=π2+21∫0(1−y2)dy
=π2+2[y−y33]10
=π2+2[1−13]
=π2+23
Topper's Solved these Questions
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Single Correct Answer Type
30 Videos
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Multiple Correct Answer Type
3 Videos
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Numerical Value Type
18 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGE PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type
2 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
Similar Questions
Let the straight line x= b divide the area enclosed by y=(1−x)2,y=0,andx=0 into two parts R1(0≤x≤b)andR2(b≤x≤1) such that R1−R2=14. Then b equals
View SolutionIf the area of bounded between the x-axis and the graph of y=6x−3x2 between the ordinates x=1andx=a is 19 units, then a can take the value 4or−2 two value are in (2,3) and one in (−1,0) two value are in (3,4) and one in (−2,−1) none of these
View SolutionThe area enclosed by the curve c:y=x√9−x2(x≥0) and the x-axis is________
View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View Solution0 <= x <= 2 pi, 0 <= y <= 2 pi and sin x + sin y = 2, quad 0 <= x <= 2 pi, 0 <= y <= 2 pi and sin x + sin y = 2, then x + y =
View SolutionThe area of the region described by A={(x,y):x^(2)+y^(2)<=1 and y^(2)<=1-x}
View SolutionThe area of the region described by A = {(x,y) : x^(2)+y^(2) le 1 and y^(2) le 1-x} is :
View SolutionFind the area of the region {(x,y):x2<y<x}
View SolutionFind the area of the region {(x,y):x2<y<|x|}
View SolutionFind the area of the region {(x,y):x2+y2<1<x+y}
(ii) Find the area of the region {(x,y):x2+y2<2ax,y2>ax,x>0,y>0}
(iii) Using integration find the area of the region {x,y):y2<4x,4x2+4y2<9}.
View SolutionThe area of the region described by {(x,y)//x^2 + y^2 le 1 and y^2 le 1-x} is
View SolutionThe area (in sq. units ) of the region A={(x,y):(x−1)[x]≤y≤2√x,0≤x≤2] where [t] denotes the greatest integer function is
View SolutionThe area (in square units) of the region enclosed by the two circles x2+y2=1and(x−1)2+y2=1 is
View SolutionThe area of the region described by : A={(x,y): x^2 +y^2 le 1 and y^2 le 1 -x } is :
View SolutionIf the regions A and B are given by A={(x,y)/:y>x}B={(x,y):y<2−x2} then the area of A∩B is
View Solution
