Area bounded by the curve [|x|]+[|y|]=3, where[.] denotes the greatest integer functionSolution in Bengali
The correct Answer is:3
[2x]=0⇒2x∈[0,1]
⇒x∈[0,1/2]⇒[y]=5⇒y∈[5,6)
Similarly we can consider [2x]=1,2,3,4and5
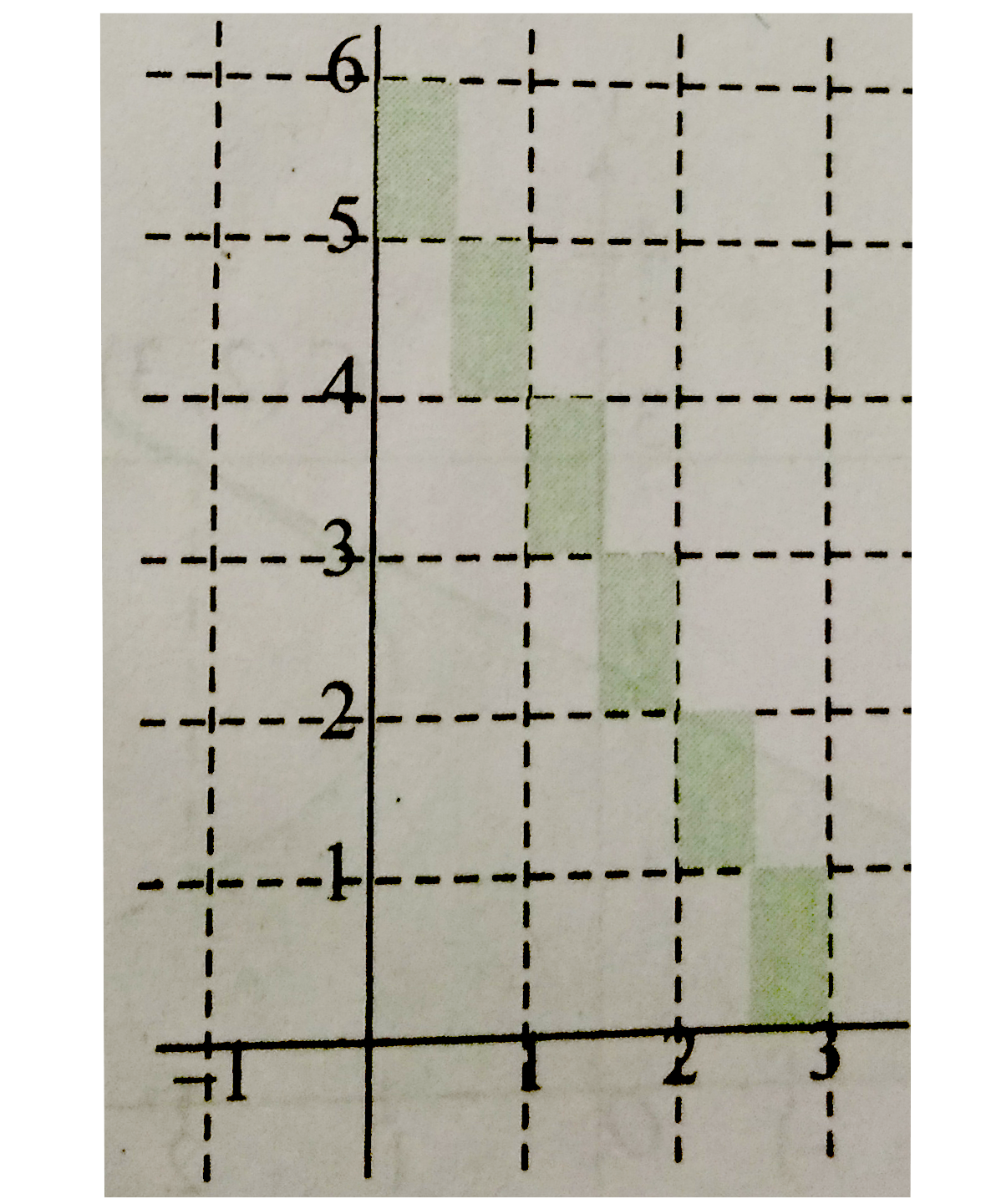
From the graph, area is 3 sq. units
Topper's Solved these Questions
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Archives
10 Videos
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Single Correct Answer Type
30 Videos
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Matrix Match Type
5 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGE PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type
2 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
Similar Questions
The area of the figure bounded by the parabola (y−2)2=x−1, the tangent to it at the point with the ordinate x=3, and the x−aξs is 7sq.unites (b) 6sq.unites 9sq.unites (d) None of these
View SolutionLet the straight line x= b divide the area enclosed by y=(1−x)2,y=0,andx=0 into two parts R1(0≤x≤b)andR2(b≤x≤1) such that R1−R2=14. Then b equals
View SolutionMatch the following lists :

View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionIf x>=0 and y>=0 ,then the area bounded by the graph of [x]+[y]=2 is (where [] denotes greatest integer function)
View SolutionArea bounded by the curve [|x|]+[|y|]=3 where [.] denotes the greatest integer function
View SolutionArea (in square units) of the region bounded by [x]2=[y]2 for x∈[1,5] ,(where [⋅] denotes the greatest integer function) is
View SolutionSketch the curves
(iii) y=∣∣[x]+√x−[x]∣∣
(where [.] denotes the greatest integer function).
(where [.] denotes the greatest integer function).
View SolutionArea of the region bounded by [x]2=[y]2,ifx∈[1,5], where [ ] denotes the greatest integer function is:
View SolutionThe area (in sq. untis) bounded by [x+y]=2 with the co - ordinate axes is equal to (where [.] denotes the greatest integer function)
View SolutionArea of the region bounded by [x]2=[y]2 ,if x∈[1,3] (where [ .] denotes the greatest integer function),is less than
View SolutionArea bounded by the curve [|x|]+[|y|]=3, where[.] denotes the greatest integer function
View SolutionThe area of the region bounded by the curve y=x2 and y=sec−1[−sin2x], (where[.] denotes the greatest integer function), is
View SolutionThe area of the reagion bounded by the curve y=[x] and the lines x=1 and x=1.9 is ……. Sq . Units . Where [.] denotes the greatest integer function .
View SolutionSketch the curves
(iii) y=∣∣[x]+√x−[x]∣∣
(where [.] denotes the greatest integer function).
(where [.] denotes the greatest integer function).
View Solution
