Question

Let f(x) be a continuous function fiven by $f\left(x\right)=\{\begin{array}{cc}2x\text{,}& \left|x\right|\le 1\\ x^2+ax+b\text{,}& \left|x\right|>1\end{array},\text{then}$
If f(x) is continuous for all real x then the value of $a^2+b^2$ is

Options

A. 3
B. 4
C. 5
D. 11

Answer

C

Explanation

`f(x)={{:(x^(2)+ax+b,xlt-1),(2x,-1lexle1),(x^(2)+ax+b,xgt1):}`
`because" "f(x) is continuous at x = -1 and x = 1`
`therefore" "(-1)^(2)+a(-1)+b=-2rArrb-a=-3" ...(1)"`
`"and "2=(1)^(2)+a.1+brArra+b=1" ...(2)"`
Solving (1) and (2), we get `a=2,b=-1`
`therefore" "f(x)={{:(x^(2)+2x-1,xlt-1),(2x,-1lexle1),(x^(2)+2x-1,xgt1):}`
Given curves are `y=f(x),x=-2y^(2) and 8x+1=0`
Solving `x=-2y^(2),y=x^(2)+2x-1(xlt-1)` we get x=-2
`"Also, "y=2x, x=-2y^(2)` meet at (0,0)
`y=2x and x=-1//8" meet at "(-(1)/(8),(-1)/(4))`
The required area is the shaded region in the figure

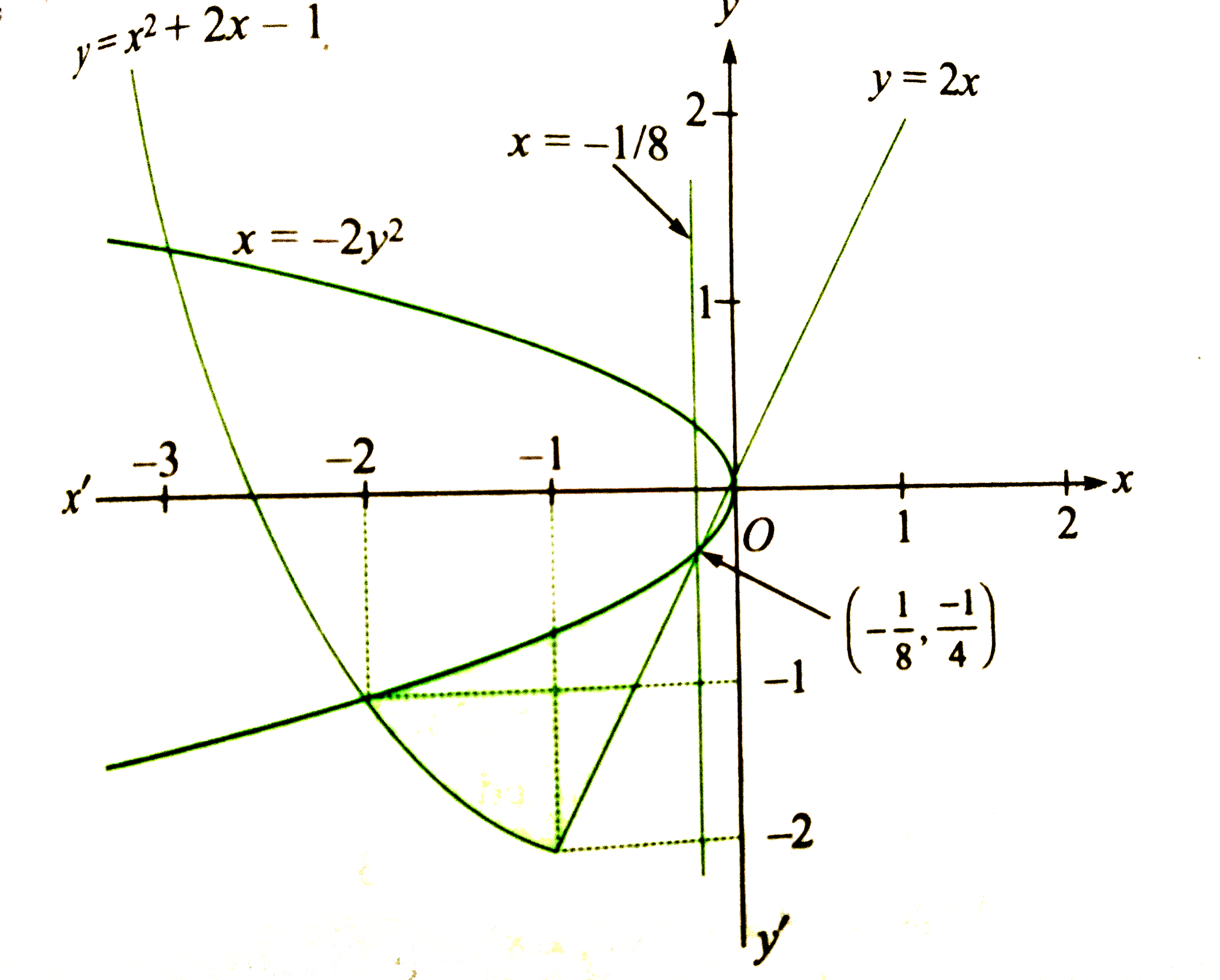
`therefore" Required area "`
`=int_(-2)^(-1)[-sqrt((-x)/(2))-(x^(2)+2x-1)dx]+int_(-1)^(-1//8)[-sqrt((-x)/(2))-2x]dx`
`=[(1)/(sqrt(2))(2(-x)^(3//2))/(3)-(x^(3))/(3)-x^(2)+x]_(-2)^(-1)+[(1)/(sqrt(2))(2(-x)^(3//2))/(3)-x^(2)]_(-1)^(-1//8)`
`=((sqrt(2))/(3)+(1)/(3)-1-1)-((4)/(3)+(8)/(3)-4-2)+((sqrt(2))/(3).(1)/(16sqrt(2))-(1)/(64))-((sqrt(2))/(3)-1)`
`=((sqrt(2)-5)/(3))-((4+8-18)/(3))+((4-3)/(192))-((sqrt(2)-3)/(3))`
`=(257)/(192)` sq. units