The area bounded by the curve xy^2 =a^2 (a−x) and y-axis isSolution in Bengali
The correct Answer is: sq. units
We have curve
The given curve is symmetrical about x-axis and meets it at (2,0).
So, y-axis is asymptote to the curve.
The graph of the function is as shown in the following figure.
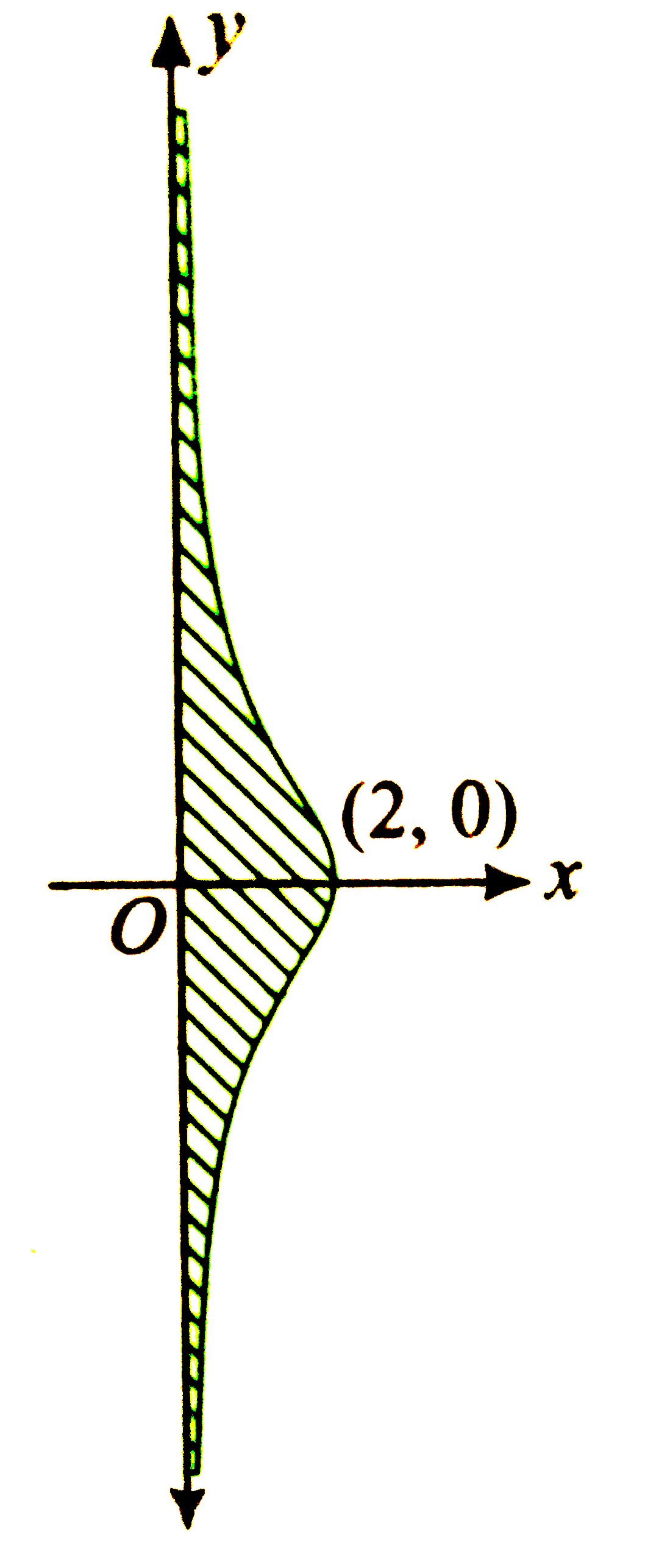
The line x=0, i.e., y-axis is asymptote.
Area of the shaded region
sq. units
Topper's Solved these Questions
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Concept Application Exercise 9.2
14 Videos
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Concept Application Exercise 9.3
7 Videos
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Solved Examples
10 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGE PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type
2 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
Similar Questions
Find the area lying in the first quadrant and bounded by the curve y=x3 and the line y=4x.
View SolutionFind the continuous function f where (x4−4x2)≤f(x)≤(2x2−x3) such that the area bounded by y=f(x),y=x4−4x2. then y-axis, and the line x=t, where (0≤t≤2) is k times the area bounded by y=f(x),y=2x2−x3,y-axis , and line x=t(where0≤t≤2).
View SolutionFind the area bounded by the curve x2=y,x2=−yandy2=4x−3
View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionFind the area bounded by the curves y=x+sqrt(x^(2)) and xy=1, the x -axis and the line x=2
View SolutionFind the area bounded by the curve xy2=4(2−x) and y-axis.
View SolutionThe area bounded by the curve a2y=x2(x+a) and the x-axis is
View SolutionThe area bounded by the curve x=2−y−y2 and Y-axis is
View SolutionArea bounded by the curve y=x2+x−6 and the X-axis is
View Solutionवक्र xy2=a2(a−x) और y- अक्ष से परिबद्ध क्षेत्रफल ज्ञात कीजिए।
View Solutionवक्र xy2=a2(a−x) एवं y- अक्ष से घिरे क्षेत्र का क्षेत्रफल होगा
View Solutionवक्र xy2=a2(a−x) एवं Y-अक्ष द्वारा परिबद्ध क्षेत्र के क्षेत्रफल का आधा है
View Solutionवक्र xy2=4(2−x) तथा Y- अक्ष से घिरे क्षेत्र का क्षेत्रफल है
View SolutionThe area bounded by the curve y=x(x2−1) and x-axis is
View SolutionThe area bounded by the curve a2y=x2(x+a) and the x-axis is
View Solution
