If the area of bounded between the x-axis and the graph of y=6x−3x2 between the ordinates x=1andx=a is 19 units, then a can take the value 4or−2 two value are in (2,3) and one in (−1,0) two value are in (3,4) and one in (−2,−1) none of theseSolution in Bengali
We have y=3x(2−x)
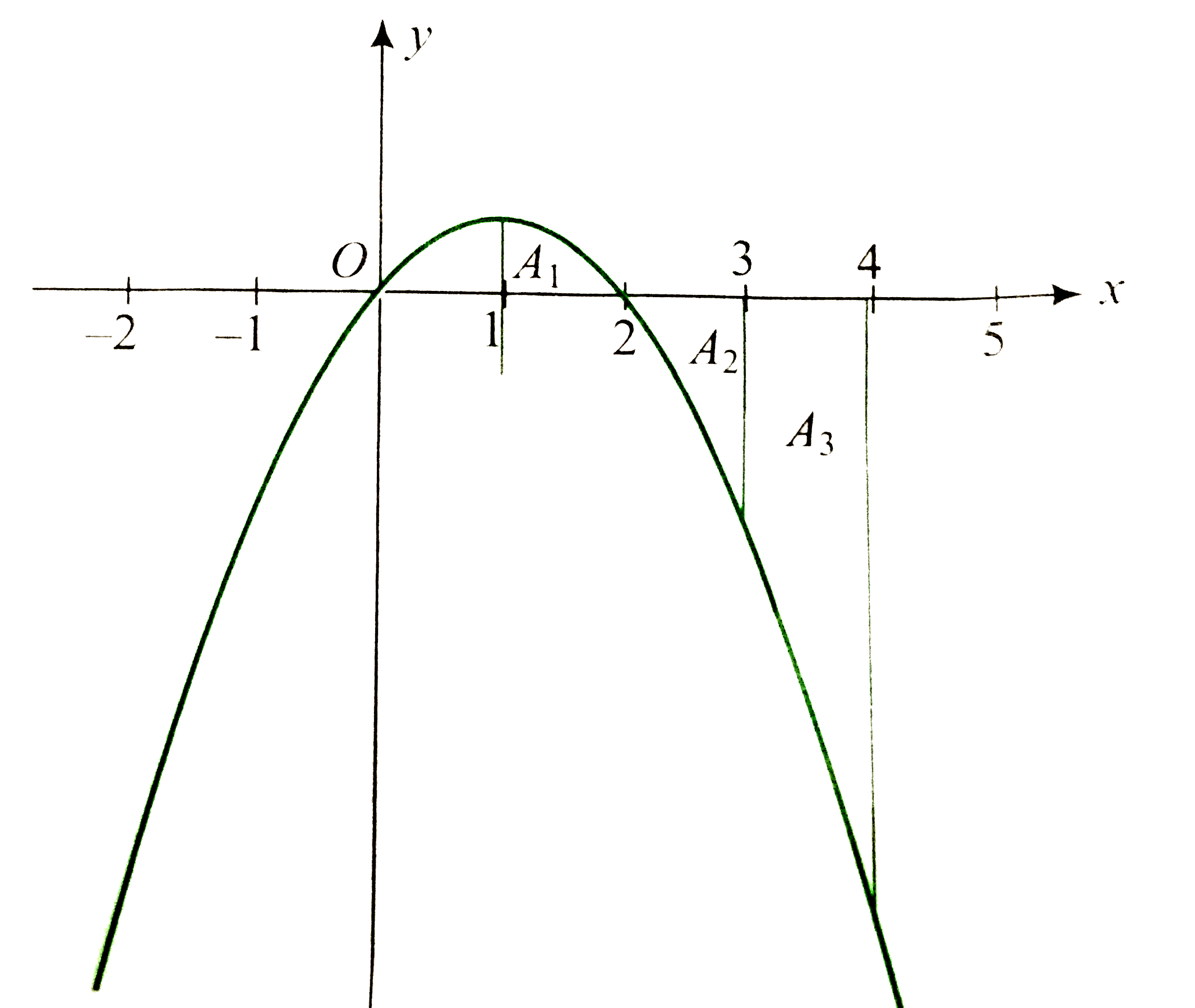
Graph of the function is downward parabola intersecting x-axis at x=0andx=2.
Now I=∫(6x−3x2)dx=6x22−3x33
3x2−x3
x2(3−x)=F(x)
Now A1=F(2)−F(1)=4−2=2sq. units
A2=F(2)−F(3)=4−0=4 sq. units
A3=F(3)−F(4)=0−(−16)=16 sq. units
Since A1+A2+A3=22 sq. units.
So,a∈(3,4)
From the symmetric of the parabola, other value of lies in (−2,−1)
Topper's Solved these Questions
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Solved Examples
10 Videos
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Concept Application Exercise 9.1
9 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGE PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type
2 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
Similar Questions
Find the area bounded by the curve x2=y,x2=−yandy2=4x−3
View SolutionFind the area of the smaller part of the circle x2+y2=a2 cut off by the line x=a√2.
View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionIf the area of bounded between the x-axis and the graph of y=6x−3x2 between the ordinates x=1 and x=a is 19 units, then a can take the value: (A) 4 or -2 (B) one value is in (2, 3) and one in (-1, 0) (C) one value is in (3, 4) and one in (-2,-1) (D) none of these
View SolutionIf the area bounded between X-axis and the graph of y=6x−3x2 between the ordinates x=1 and x=a is 10sq units, then 'a' can take the value
View SolutionThe area bounded by y=(x2−x)2 with the x - axis, between its two relative minima, is A sq, units, the value of 15A is equal to
View Solution(i) Find the area bounded by y=3x+2, the x-axis and the ordinates x=−2andx=1.
(ii) Find the area bounded by y=x, the x-axis and the line x=−1andx=2.
View SolutionThe area bounded by the curve y=x3 , x-axis and two ordinates x=1 and x=2 is equals to :
View SolutionThe area bounded by y=x2−1,x- axis and with ordinates x=2,x=4 is ( in square units)
View Solutionযদি y=ax2 এবং x=ay2,a>0 অধিবৃত্ত দুটি দ্বারা সীমাবদ্ধ অঞ্চলে ক্ষেত্রফল 1 বর্গএকক হয়, তবে a-এর মান হবে-
View SolutionIf the area of bounded between the x-axis and the graph of y=6x−3x2 between the ordinates x=1 and x=a is 19 units, then a can take the value: (A) 4 or -2 (B) one value is in (2, 3) and one in (-1, 0) (C) one value is in (3, 4) and one in (-2,-1) (D) none of these
View SolutionIf the area of bounded between the x-axis and the graph of y=6x−3x2 between the ordinates x=1andx=a is 19 units, then a can take the value 4or−2 two value are in (2,3) and one in (−1,0) two value are in (3,4) and one in (−2,−1) none of these
View SolutionIf the area of bounded between the x-axis and the graph of y=6x−3x2 between the ordinates x=1andx=a is 19 units, then a can take the value 4or−2 two value are in (2,3) and one in (−1,0) two value are in (3,4) and one in (−2,−1) none of these
View SolutionIf the curve y = sqrt(3x+4) The area of the area bounded between the line x = - 1 and x = 4 and x - axis is A and the curve y^(2)=3x+4 , Is the area of the area bounded between the line x = - 1 and x = 4 and the axis, then the value of A: B is
View SolutionFind the area of the region bounded by y=6x−x2x-axis and between ordinates x = 0 and x = 6.
View Solution
