The graph of the derivative f'(x) is given in the following figure.
(a) Find the interval in which f is increasing or decreasing.
(b) Find the values of x for which f has local maximum or minimum.
(c) Find the intervals in which f is concave upward or downward.
(c) Find the point of inflection.
 Solution in Bengali
Solution in Bengali
We have f:R→[1,∞),f(x)=x2−4x+5
or f(x)=(x−2)2+1.
Graph of the function is as shown in the following figure.
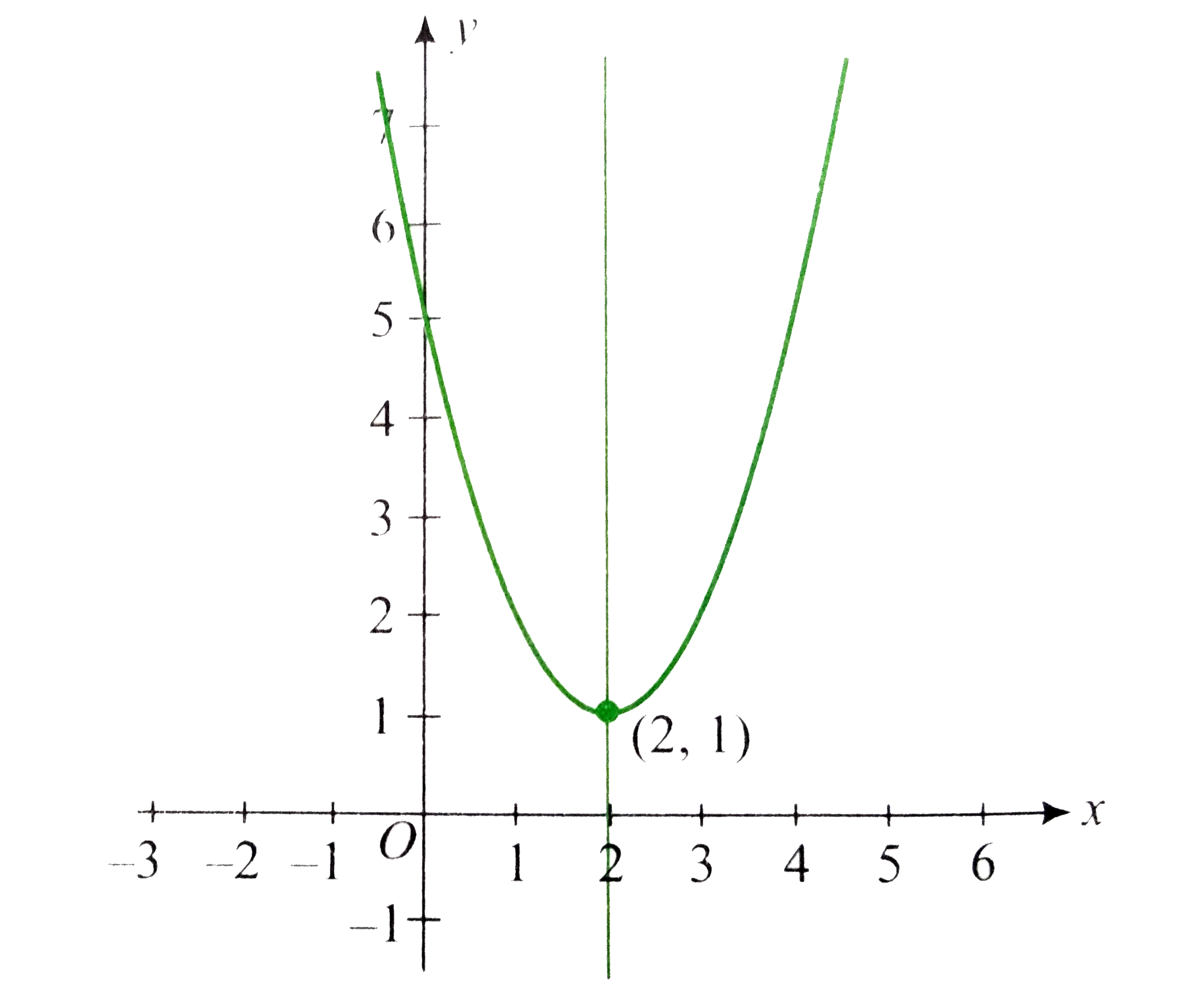
Clearly f(x) is many-one function.
However, in the interval (−∞,2]or[2,∞),f(x) is one-one.
For f:(−∞,2]→[1,∞),y=(x−2)2+1
∴(x−2)2=y−1
⇒x−2=√y−1
⇒x=2−√y−1
Thus f−1:[1,∞)→(−∞,2],f−1(x)=2−√x−1
For f:[2,∞)→[1,∞),y=(x−2)2+1
⇒x=2+√y−1
Thus f−1:[1,∞)→[2,∞),f−1(x)=√x−1+2
Topper's Solved these Questions
Similar Questions
Let ABCandABC' be two non-congruent triangles with sides AB=4,AC=AC′=2√2 and angle B=300 . The absolute value of the difference between the areas of these triangles is
View SolutionNumber of integral value(s) of λ for which vectors x2ˆi−ˆj+xˆk,(λ−1)ˆi−2λˆj−ˆk and ˆi−ˆj+ˆk, in the order form right-handed system ∀x ∈R, is
(a) 0 (b) 2 (c) 4 (d) 6
View SolutionThe graph of the derivative f'(x) is given in the following figure.
(b) Find the values of x for which f has local maximum or minimum.
(c) Find the intervals in which f is concave upward or downward.
(d) Find the point of inflection.
(##CEN_GRA_C01_S01_023_Q01.png" width="80%">
View SolutionThe graph of the derivative f'(x) is given in the following figure.
(a) Find the interval in which f is increasing or decreasing.
(b) Find the values of x for which f has local maximum or minimum.
(c) Find the intervals in which f is concave upward or downward.
(c) Find the point of inflection.

View SolutionIn the given figure (not to scale), O is the centre of the circle. A,B,C and D are concyclic and AB=CD . If /_MON =120^(@) , then find /_ OPN .
View SolutionMatch the following Column A to Column B

View SolutionFind the area of figure given below.
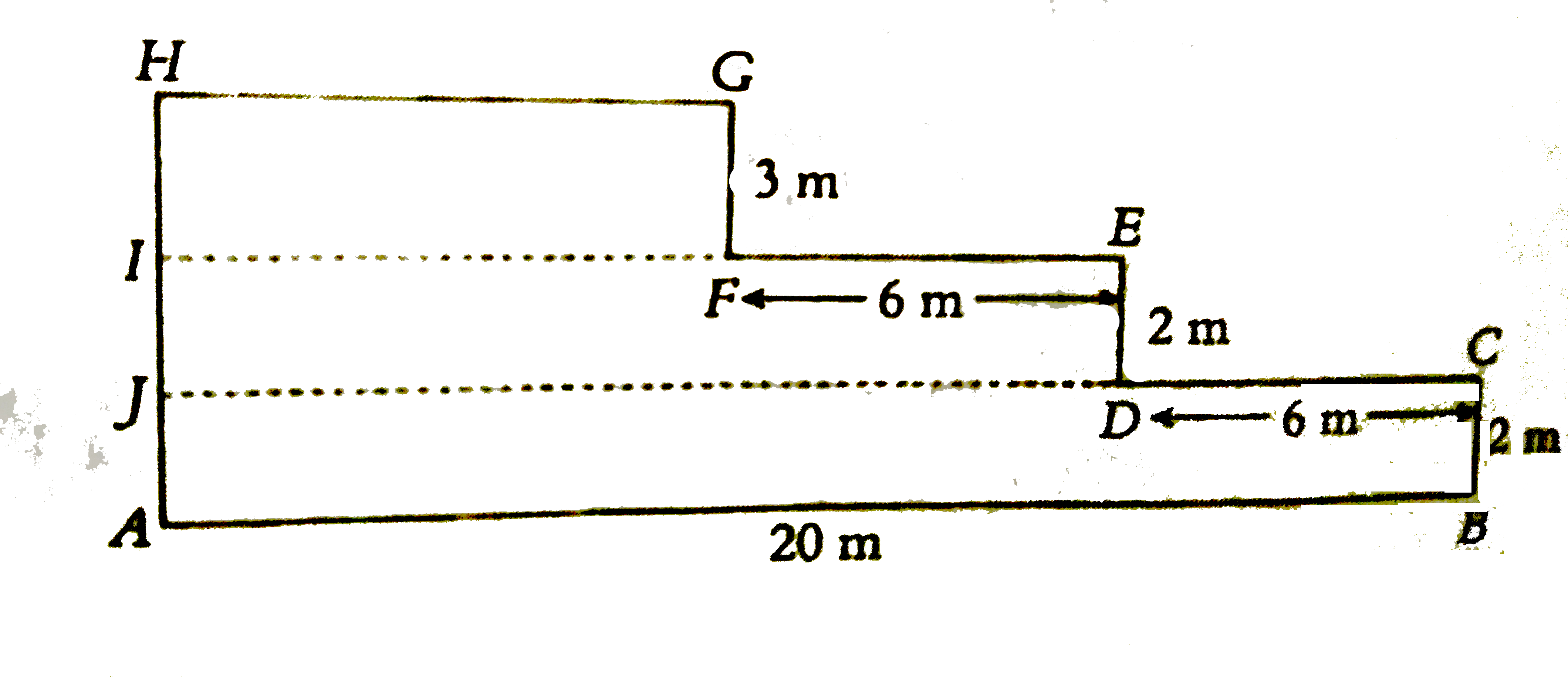
View SolutionFind the perimeter of the figure given below.
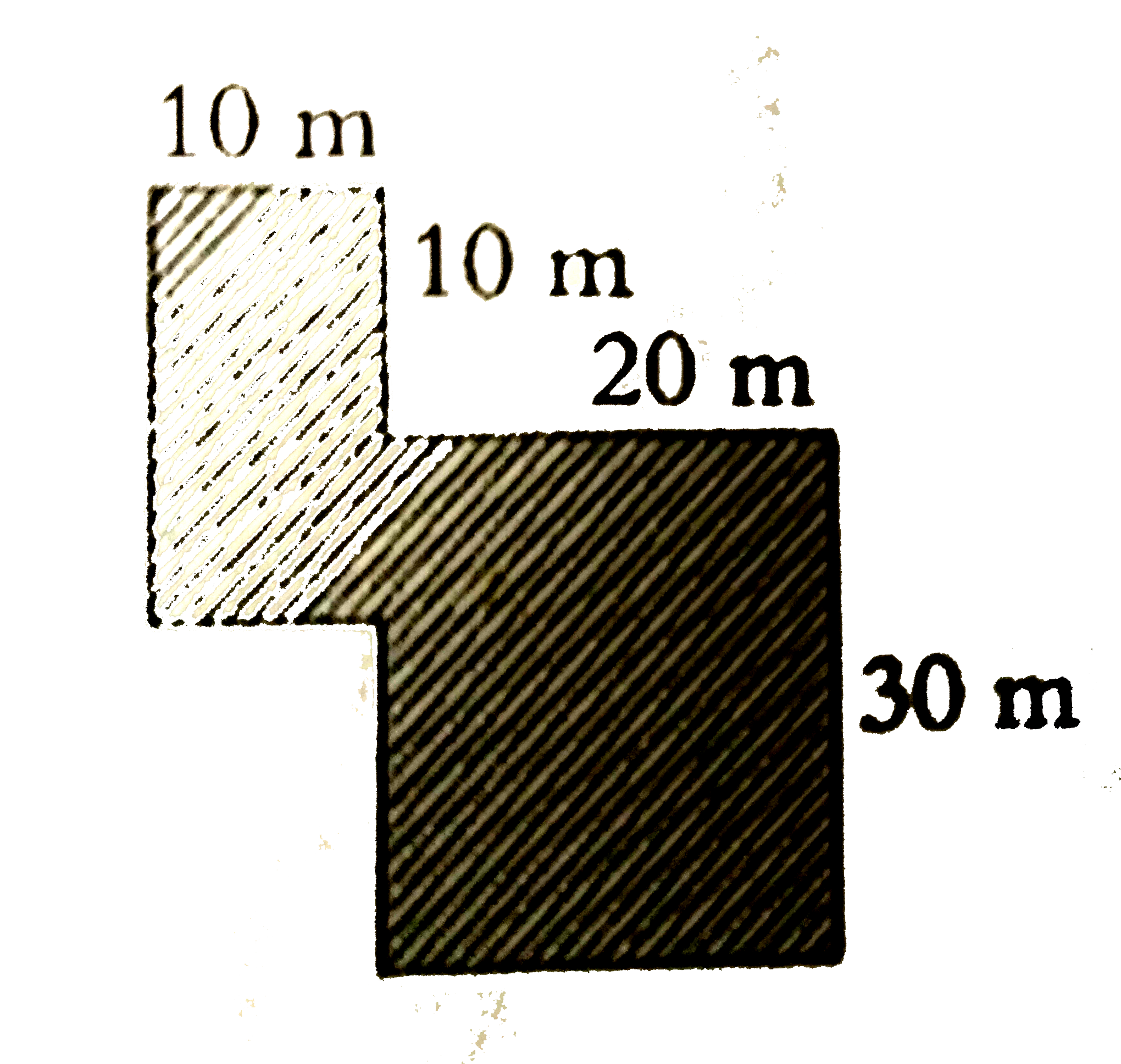
View SolutionFind the area of the figure given below.
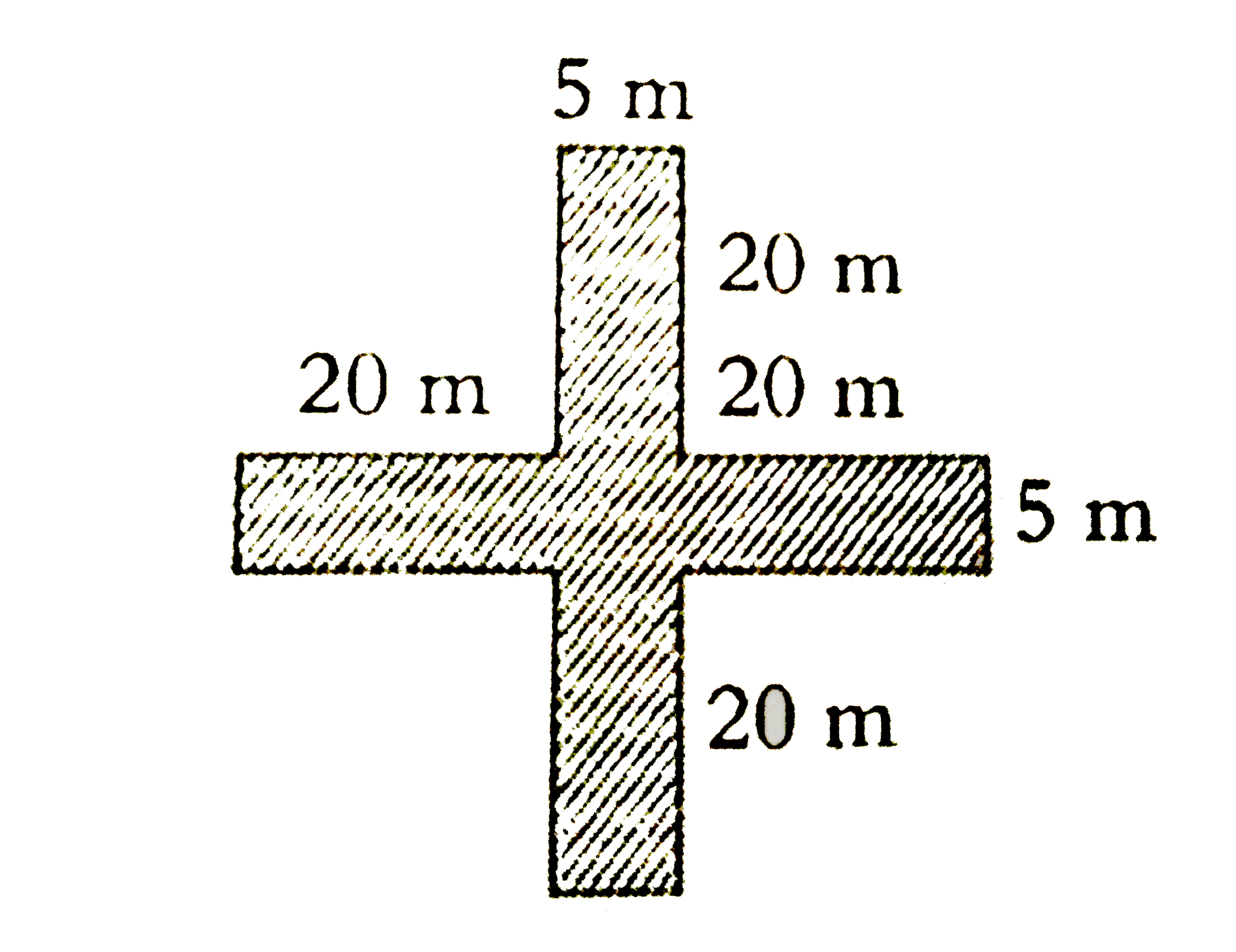
View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionWhich inequations represent the shaded region in the given figure
View SolutionIn Fig, find the value of x.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_S01_032_Q01.png" width="80%"gt
View SolutionIn the given figure, PQRS is a parallelogram. A and B are the mid-point of ¯¯¯¯¯¯PQ and ¯¯¯¯¯SR respectively. If PS=BR, then the quadrilateral ADBC is a…………………… ,
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E05_020_Q01.png" width="80%"gt
View SolutionWhich has maximum XCX bond angle ? (X=F,Cl,Br)
View Solution
